《2025年暑假生活五年级上海教育出版社》

1. 下列图形都是用$1cm^{3}$的正方体搭成的,分别写出它们的体积。

体积是( ) 体积是( ) 体积是( )

答案： 【解析】：
1. 第一个图形：通过观察可知，它是一个长$3cm$、宽$3cm$、高$1cm$的长方体，根据长方体体积公式$V = a\times b\times h$（其中$a$为长，$b$为宽，$h$为高），可得体积为$3×3×1 = 9cm^{3}$。
2. 第二个图形：可以分层数，底层有$4$个小正方体，上层有$2$个小正方体，一共有$4 + 2 = 6$个小正方体，每个小正方体体积是$1cm^{3}$，所以体积是$6×1 = 6cm^{3}$。
3. 第三个图形：同样分层数，底层有$9$个小正方体，中间层有$4$个小正方体，上层有$1$个小正方体，一共有$9 + 4 + 1 = 14$个小正方体，体积是$14×1 = 14cm^{3}$。
【答案】：$9cm^{3}$ $6cm^{3}$ $14cm^{3}$

2. 估计下列图形的面积(每个小方格的面积表示$1cm^{2}$)。

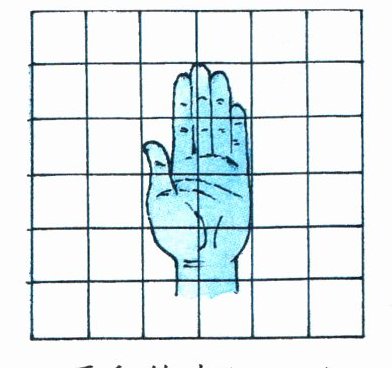
面积约为( ) 面积约为( )

答案： 【解析】：本题可通过数方格的方法来估计图形面积，不满一格的按半格计算。
先数满格的，再数不满格的。
满格有$4$个，不满格有$12$个。
因为每个小方格面积是$1cm^{2}$，不满一格按半格算，所以图形面积为$4 + 12÷2 = 4 + 6 = 10(cm^{2})$。
【答案】：$10cm^{2}$

3. 求下列图形中阴影部分的面积。

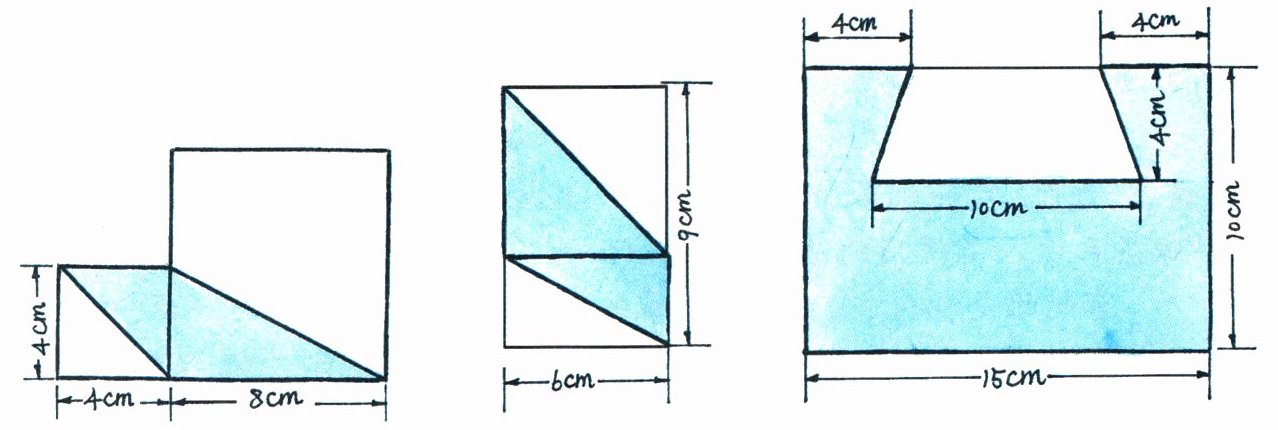
答案： 【解析】：
第一个图形：
阴影部分面积等于两个三角形面积之和。
左边三角形面积：$S_1=\frac{1}{2}\times4\times4 = 8$（$cm^2$）。
右边三角形面积：$S_2=\frac{1}{2}\times8\times4 = 16$（$cm^2$）。
阴影部分总面积：$S = S_1+S_2=8 + 16=24$（$cm^2$）。
第二个图形：
阴影部分面积等于两个三角形面积之和。
上面三角形面积：$S_1=\frac{1}{2}\times6\times(9 - 6)=9$（$cm^2$）。
下面三角形面积：$S_2=\frac{1}{2}\times6\times6 = 18$（$cm^2$）。
阴影部分总面积：$S = S_1+S_2=9+18 = 27$（$cm^2$）。
第三个图形：
阴影部分面积等于长方形面积减去梯形面积。
长方形面积：$S_{长}=15\times10 = 150$（$cm^2$）。
梯形的上底为$15 - 4 - 4=7$（$cm$），下底为$10cm$，高为$4cm$。
梯形面积：$S_{梯}=\frac{(7 + 10)\times4}{2}=34$（$cm^2$）。
阴影部分总面积：$S = S_{长}-S_{梯}=150-34 = 116$（$cm^2$）。
【答案】：24$cm^2$，27$cm^2$，116$cm^2$