《2025年暑假作业长江少年儿童出版社四年级数学》

5)
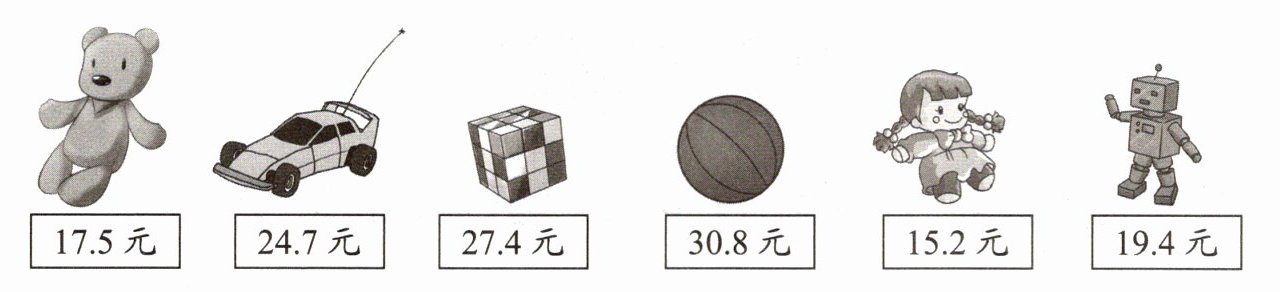
(1)聪聪给弟弟买了一只玩具熊和一个布娃娃,明明给妹妹买了一个皮球,谁花的钱多? 多多少元?
(2)玲玲带了$50$元钱,想买三件不同的玩具。钱够吗?

答案： 本题可根据图中玩具价格，分别计算出聪聪和明明的花费，再进行比较；对于第二问，找出价格最低的三件玩具计算总价，再与$50$元比较。
$(1)$计算聪聪和明明的花费并比较
- **步骤一：计算聪聪的花费
已知玩具熊$17.5$元，布娃娃$15.2$元，根据加法的意义，将两者价格相加可得聪聪的花费：
$17.5 + 15.2=32.7$（元）
- **步骤二：计算明明的花费
已知皮球$30.8$元，即明明花费$30.8$元。
- **步骤三：比较两人花费并计算差值
比较$32.7$与$30.8$的大小，可得$32.7＞30.8$，所以聪聪花的钱多。
再根据减法的意义，计算多的金额：
$32.7 - 30.8 = 1.9$（元）
$(2)$判断玲玲带的钱是否够买三件不同玩具
要判断$50$元够不够买三件不同的玩具，可先找出价格最低的三件玩具，即玩具熊$17.5$元、布娃娃$15.2$元、机器人$19.4$元。
根据加法的意义，计算这三件玩具的总价：
$17.5 + 15.2 + 19.4$
$=32.7 + 19.4$
$= 52.1$（元）
比较$52.1$与$50$的大小，可得$52.1＞50$，所以钱不够。
综上，答案依次为：$(1)$ **聪聪花的钱多，多$1.9$元**；$(2)$ **钱不够**。

想一想,做一做。
(1)如果一个三角形两条边的长分别是$5厘米和8$厘米,那么这个三角形的第三条边的长可能是多少厘米? (取整厘米数)
(2)一个直角三角形中,较大锐角是较小锐角的$2$倍。求这两个锐角各是多少度。
(3)一个等腰三角形中有一个角是$60$度,那它其他两个角各是多少度? 它又是什么三角形?

答案：
(1)
解析：
题目考查三角形三边关系的知识点，即任意两边之和大于第三边，任意两边之差小于第三边。
设第三边的长为$x$厘米，根据三角形三边关系可得：
$8 - 5 \lt x \lt 8 + 5$，
即$3 \lt x \lt 13$。
因为$x$取整厘米数，所以$x$可能是$4$、$5$、$6$、$7$、$8$、$9$、$10$、$11$、$12$。
答案：
第三条边的长可能是$4$、$5$、$6$、$7$、$8$、$9$、$10$、$11$、$12$厘米。
(2)
解析：
题目考查直角三角形两锐角和为$90^{\circ}$的知识点。
设较小锐角为$x$度，则较大锐角为$2x$度，根据直角三角形两锐角和为$90^{\circ}$，可得方程$x + 2x = 90$。
解方程过程：
$3x = 90$，
$x = 90÷3$，
$x = 30$。
则较大锐角为$2x = 2×30 = 60$。
答案：
较小锐角是$30$度，较大锐角是$60$度。
(3)
解析：
题目考查等腰三角形性质的知识点，即等腰三角形两底角相等。
分情况讨论：
当$60^{\circ}$角为顶角时，根据三角形内角和为$180^{\circ}$以及等腰三角形两底角相等，可得底角为$(180 - 60)÷2 = 60$度，此时三个角都是$60^{\circ}$，是等边三角形。
当$60^{\circ}$角为底角时，另一个底角也是$60^{\circ}$，则顶角为$180 - 60×2 = 60$度，同样是等边三角形。
答案：
其他两个角都是$60$度，它是等边三角形。