《2025年暑假作业长江少年儿童出版社四年级数学》

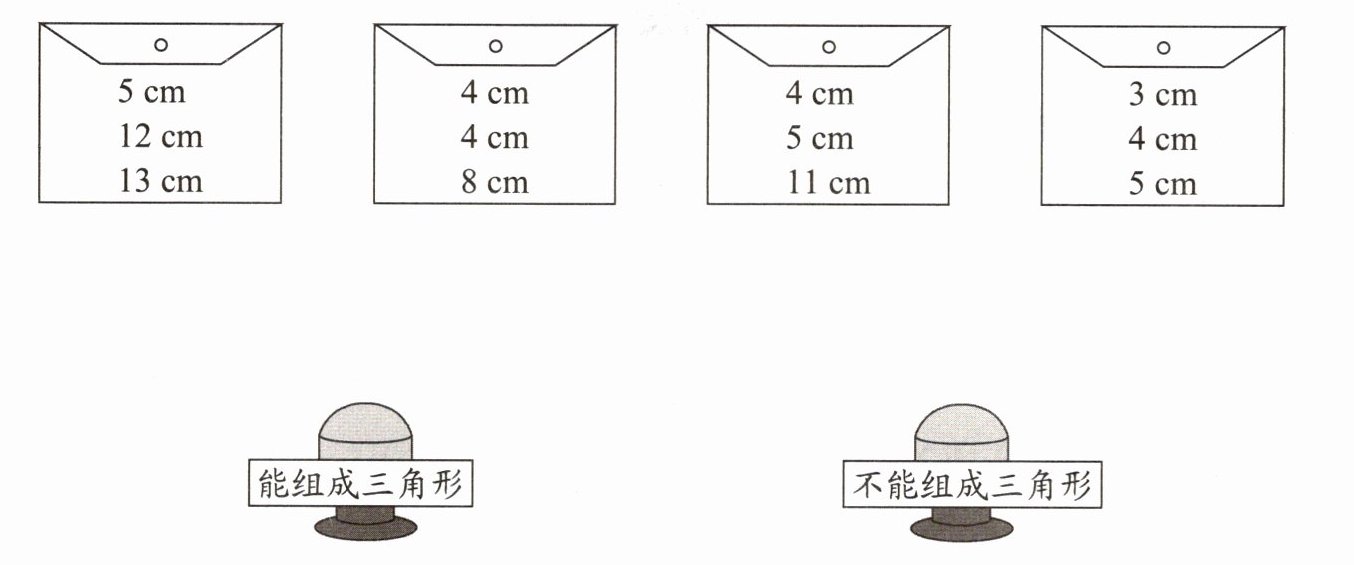
4) 每个信封上的三条线段能否组成一个三角形？用线连一连。

答案： 本题可根据三角形三边关系“任意两边之和大于第三边，任意两边之差小于第三边”来判断每组线段能否组成三角形。
第一组线段：5cm、12cm、13cm
判断较短两边之和与最长边的大小关系：
$5 + 12 = 17\gt 13$
再判断任意两边之差与第三边的大小关系：
$13 - 5 = 8\lt 12$
$13 - 12 = 1\lt 5$
$12 - 5 = 7\lt 13$
满足三角形三边关系，所以能组成三角形，应与下面的“能组成三角形”相连。
第二组线段：4cm、4cm、8cm
判断较短两边之和与最长边的大小关系：
$4 + 4 = 8$，并不大于8。
不满足三角形三边关系，所以不能组成三角形，应与下面的“不能组成三角形”相连。
第三组线段：4cm、5cm、11cm
判断较短两边之和与最长边的大小关系：
$4 + 5 = 9\lt 11$
不满足三角形三边关系，所以不能组成三角形，应与下面的“不能组成三角形”相连。
第四组线段：3cm、4cm、5cm
判断较短两边之和与最长边的大小关系：
$3 + 4 = 7\gt 5$
再判断任意两边之差与第三边的大小关系：
$5 - 3 = 2\lt 4$
$5 - 4 = 1\lt 3$
$4 - 3 = 1\lt 5$
满足三角形三边关系，所以能组成三角形，应与下面的“能组成三角形”相连。
综上，5cm、12cm、13cm和3cm、4cm、5cm这两组线段能与“能组成三角形”相连；4cm、4cm、8cm和4cm、5cm、11cm这两组线段能与“不能组成三角形”相连。

5) 画一个底角是$60^{\circ}$的等腰三角形。再算一算,这个三角形的顶角和另一个底角分别是多少度？如果按角分类,它是什么三角形？如果按边分类,它是什么三角形？

答案： 解析：
题目要求画一个底角是$60^\circ$的等腰三角形，并计算顶角和另一个底角的度数，然后根据角度和边长对三角形进行分类。
等腰三角形的两个底角相等，所以另一个底角也是$60^\circ$。
三角形内角和为$180^\circ$，所以顶角的度数为$180^\circ - 60^\circ - 60^\circ = 60^\circ$。
根据角度分类，三个角都小于$90^\circ$，所以是锐角三角形。
根据边长分类，有两个角相等，所以对应的两边也相等，是等腰三角形。而三个角都相等，说明三边也相等，因此也是等边三角形。
答案：
图略
顶角：$60^\circ$，另一个底角：$60^\circ$。
按角分类：锐角三角形。
按边分类：等边三角形（也是等腰三角形的一种特殊情况）。

如下图所示,等边三角形内有一个等腰三角形,并且$∠1= ∠2$,$∠3= ∠4$,你能求出$∠5$的度数吗？
$\angle5 = 120^{\circ}$

答案： 解析：已知大三角形是等边三角形，根据等边三角形的性质，其三个内角都相等且为$60^{\circ}$，所以可得$\angle1 + \angle2 + \angle3 + \angle4 = 180^{\circ}-60^{\circ}=120^{\circ}$。
因为$\angle1 = \angle2$，$\angle3 = \angle4$，所以$\angle2 + \angle4=120^{\circ}÷2 = 60^{\circ}$。
最后根据三角形内角和为$180^{\circ}$，可求出$\angle5$的度数为$180^{\circ}-60^{\circ}=120^{\circ}$。
答案：$\angle5 = 120^{\circ}$。