《2025年巅峰对决九年级数学上册人教版》

2.如图,在平面直角坐标系中,$\odot O$的半径为1,则直线$y= x-\sqrt{2}与\odot O$的位置关系是 (B)
A.相离
B.相切
C.相交
D.以上三种情况都有可能

答案： 解：圆心O(0,0)，半径r=1。
直线方程：x - y - √2 = 0。
圆心到直线距离d = |0 - 0 - √2| / √(1² + (-1)²) = √2 / √2 = 1。
∵d = r，
∴直线与⊙O相切。
答案：B

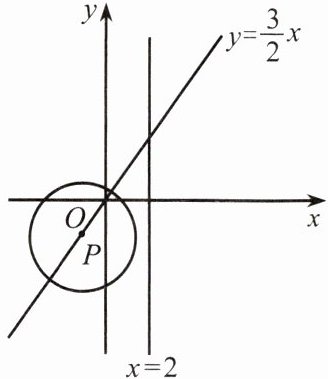
例2 如图,$P为正比例函数y= \frac{3}{2}x$图象上的一个动点,$\odot P$的半径为3,设点$P的坐标为(x,y)$.
(1)求$\odot P与直线x= 2相切时点P$的坐标;
(2)请直接写出$\odot P与直线x= 2$相交、相离时$x$的取值范围.
分析:(1)由圆与直线相切时圆心到直线的距离等于半径可知,应先找圆心到直线$x= 2$的距离刚好为3时的横坐标,再代入$y= \frac{3}{2}x$得纵坐标;(2)借助(1)题中的结论容易得解.

答案：
(1)解：因为圆心$P(x,y)$到直线$x=2$的距离为$|x - 2|$，$\odot P$与直线$x=2$相切时，距离等于半径$3$，所以$|x - 2| = 3$。
当$x - 2 = 3$时，$x = 5$，代入$y = \frac{3}{2}x$，得$y = \frac{3}{2}×5 = \frac{15}{2}$，此时点$P$的坐标为$(5, \frac{15}{2})$；
当$x - 2 = -3$时，$x = -1$，代入$y = \frac{3}{2}x$，得$y = \frac{3}{2}×(-1) = -\frac{3}{2}$，此时点$P$的坐标为$(-1, -\frac{3}{2})$。
综上，点$P$的坐标为$(5, \frac{15}{2})$或$(-1, -\frac{3}{2})$。
(2)相交时$x$的取值范围：$-1 ＜ x ＜ 5$；相离时$x$的取值范围：$x ＜ -1$或$x ＞ 5$。

3.已知$\odot O$的直径为12$\ \text{cm}$,圆心$O到直线l$的距离为5$\ \text{cm}$,则直线$l与\odot O$的交点个数为2.

答案： 【解析】：
本题考查的是直线与圆的位置关系。
首先明确直线与圆的三种位置关系：
如果圆心到直线的距离小于圆的半径，那么直线与圆相交，有两个交点。
如果圆心到直线的距离等于圆的半径，那么直线与圆相切，有一个交点。
如果圆心到直线的距离大于圆的半径，那么直线与圆相离，没有交点。
根据题目已知圆的直径为$12\text{cm}$，所以半径$r = \frac{12}{2} = 6\text{cm}$。
圆心到直线$l$的距离为$5\text{cm}$，由于$5\text{cm} ＜ 6\text{cm}$，即圆心到直线的距离小于圆的半径。
根据直线与圆的位置关系，当圆心到直线的距离小于圆的半径时，直线与圆相交，所以直线$l$与$\odot O$相交，因此有两个交点。
【答案】：
2

4.在$\text{Rt}\triangle ABC$中,$\angle A= 30^{\circ}$,直角边$AC= 6\ \text{cm}$,以点$C$为圆心,$3\ \text{cm}$长为半径作圆,则$\odot C与AB$的位置关系是相切.

答案： 解：过点$C$作$CD \perp AB$于点$D$。
在$\text{Rt}\triangle ABC$中，$\angle A = 30^{\circ}$，$AC = 6\ \text{cm}$，
$\because \sin A=\dfrac{CD}{AC}$，
$\therefore CD=AC\cdot\sin A=6×\sin30^{\circ}=6×\dfrac{1}{2}=3\ \text{cm}$。
$\because \odot C$的半径为$3\ \text{cm}$，即圆心$C$到直线$AB$的距离$d = 3\ \text{cm}$等于半径$r$，
$\therefore \odot C$与$AB$的位置关系是相切。

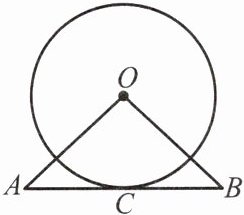
例 1 如图,已知直线AB经过$\odot O$上的点C,$OA= OB,CA= CB$.求证:直线AB是$\odot O$的切线.
分析:AB经过$\odot O$上的点C,如果连接OC,那么就满足了"经过半径的外端"这一条件,接着根据切线的判定定理,只要再证明$OC⊥AB$即可.

归纳：
(1)判断圆的切线的常用方法：
①和圆只有一个公共点的直线是圆的切线；
②和圆心的距离等于半径的直线是圆的切线；
③经过半径外端且垂直于半径的直线是圆的切线.
(2)证明圆的切线的常用方法：
①公共点已给定:连接半径,证明半径垂直于该直线,简记为"连半径,证垂直".
②公共点未给定:从圆心向直线作垂线段,证明垂线段的长等于半径,简记为"作垂直,证半径".

答案： 【解析】：本题主要考察了圆的切线的判定定理，即经过半径的外端且垂直于这条半径的直线是圆的切线。
连接$OC$。
由于$OA = OB$且$CA = CB$，根据等腰三角形的性质，我们知道底边上的中线、底边上的高线和顶角的角平分线是重合的。
因此，$OC$作为等腰三角形$OAB$底边$AB$上的中线，同时也是高线，即$OC \perp AB$。
由于点C在圆O上，所以线段$OC$是圆$O$的半径。
根据圆的切线的判定定理，经过半径$OC$的外端C且垂直于半径$OC$的直线$AB$是圆$O$的切线。
【答案】：证明：
连接$OC$。
∵$OA = OB$，$CA = CB$，
∴$OC \perp AB$，
∵$OC$为$ \odot O$的半径，
∴直线$AB$是$ \odot O$的切线。