7.下列关于抛物线$y= -(x+1)^{2}+4$的判断中,错误的是(
A.形状与抛物线$y= -x^{2}$相同
B.对称轴是直线$x= -1$
C.当y随x的增大而减小时,$x>0$
D.当$y>0$时,$-3<x<1$
C
)A.形状与抛物线$y= -x^{2}$相同
B.对称轴是直线$x= -1$
C.当y随x的增大而减小时,$x>0$
D.当$y>0$时,$-3<x<1$
答案:
【解析】:
本题考察二次函数$y=a(x-h)^2+k$的图象和性质。
对于选项A,由于抛物线$y= -(x+1)^{2}+4$与$y= -x^{2}$的二次项系数相同,所以它们的形状相同,只是位置有所不同。因此,选项A是正确的。
对于选项B,由二次函数的性质,抛物线$y=a(x-h)^2+k$的对称轴是$x=h$。
所以,抛物线$y= -(x+1)^{2}+4$的对称轴是$x=-1$。因此,选项B是正确的。
对于选项C,需要判断y随x的增大而减小的区间。
由于抛物线的开口向下(因为二次项系数为负),并且对称轴是$x=-1$,所以当$x>-1$时,y随x的增大而减小。
因此,选项C中的“当y随x的增大而减小时,$x>0$”是错误的,应该是$x>-1$。
对于选项D,需要找出使得$y>0$的x的取值范围。
解不等式$-(x+1)^2+4>0$,可以得到$-3<x<1$。因此,选项D是正确的。
【答案】:
C
本题考察二次函数$y=a(x-h)^2+k$的图象和性质。
对于选项A,由于抛物线$y= -(x+1)^{2}+4$与$y= -x^{2}$的二次项系数相同,所以它们的形状相同,只是位置有所不同。因此,选项A是正确的。
对于选项B,由二次函数的性质,抛物线$y=a(x-h)^2+k$的对称轴是$x=h$。
所以,抛物线$y= -(x+1)^{2}+4$的对称轴是$x=-1$。因此,选项B是正确的。
对于选项C,需要判断y随x的增大而减小的区间。
由于抛物线的开口向下(因为二次项系数为负),并且对称轴是$x=-1$,所以当$x>-1$时,y随x的增大而减小。
因此,选项C中的“当y随x的增大而减小时,$x>0$”是错误的,应该是$x>-1$。
对于选项D,需要找出使得$y>0$的x的取值范围。
解不等式$-(x+1)^2+4>0$,可以得到$-3<x<1$。因此,选项D是正确的。
【答案】:
C
8.(2023·襄阳)如图,一位篮球运动员投篮时,球从点A处出手后沿抛物线行进,篮球出手后距离地面的高度y(m)与篮球距离出手点的水平距离x(m)之间的函数解析式是$y= -\frac{1}{5}(x-\frac{3}{2})^{2}+\frac{7}{2}$.下列说法正确的是______(填序号).
①篮球行进过程中距离地面的最大高度为3.5m;
②篮球出手点距离地面的高度为2.25m.

①篮球行进过程中距离地面的最大高度为3.5m;
②篮球出手点距离地面的高度为2.25m.

①
答案:
1. 首先分析①:
对于抛物线$y = a(x - h)^{2}+k(a\neq0)$,当$a\lt0$时,抛物线开口向下,顶点坐标为$(h,k)$,函数在$x = h$处取得最大值$k$。
在函数$y=-\frac{1}{5}(x - \frac{3}{2})^{2}+\frac{7}{2}$中,$a =-\frac{1}{5}\lt0$,$h=\frac{3}{2}$,$k = \frac{7}{2}$。
因为$\frac{7}{2}=3.5$,所以篮球行进过程中距离地面的最大高度为$3.5m$,故①**正确**。
2. 然后分析②:
当$x = 0$时(此时$x = 0$表示篮球出手点的水平距离),把$x = 0$代入$y=-\frac{1}{5}(x - \frac{3}{2})^{2}+\frac{7}{2}$中。
则$y=-\frac{1}{5}(0 - \frac{3}{2})^{2}+\frac{7}{2}$。
根据运算顺序,先计算$(0-\frac{3}{2})^{2}=\frac{9}{4}$,那么$-\frac{1}{5}(0 - \frac{3}{2})^{2}+\frac{7}{2}=-\frac{1}{5}×\frac{9}{4}+\frac{7}{2}$。
通分可得$y=-\frac{9}{20}+\frac{70}{20}=\frac{-9 + 70}{20}=\frac{61}{20}=3.05(m)$,所以篮球出手点距离地面的高度为$3.05m$,故②**错误**。
综上,答案为①。
对于抛物线$y = a(x - h)^{2}+k(a\neq0)$,当$a\lt0$时,抛物线开口向下,顶点坐标为$(h,k)$,函数在$x = h$处取得最大值$k$。
在函数$y=-\frac{1}{5}(x - \frac{3}{2})^{2}+\frac{7}{2}$中,$a =-\frac{1}{5}\lt0$,$h=\frac{3}{2}$,$k = \frac{7}{2}$。
因为$\frac{7}{2}=3.5$,所以篮球行进过程中距离地面的最大高度为$3.5m$,故①**正确**。
2. 然后分析②:
当$x = 0$时(此时$x = 0$表示篮球出手点的水平距离),把$x = 0$代入$y=-\frac{1}{5}(x - \frac{3}{2})^{2}+\frac{7}{2}$中。
则$y=-\frac{1}{5}(0 - \frac{3}{2})^{2}+\frac{7}{2}$。
根据运算顺序,先计算$(0-\frac{3}{2})^{2}=\frac{9}{4}$,那么$-\frac{1}{5}(0 - \frac{3}{2})^{2}+\frac{7}{2}=-\frac{1}{5}×\frac{9}{4}+\frac{7}{2}$。
通分可得$y=-\frac{9}{20}+\frac{70}{20}=\frac{-9 + 70}{20}=\frac{61}{20}=3.05(m)$,所以篮球出手点距离地面的高度为$3.05m$,故②**错误**。
综上,答案为①。
|二次函数|开口方向|对称轴|顶点坐标|
|$y= 2(x+3)^{2}+5$|
|$y= -3(x-1)^{2}-2$|
|$y= 4(x-3)^{2}+7$|
|$y= -5(x+2)^{2}-6$|
|$y= 2(x+3)^{2}+5$|
向上
|直线$x = - 3$
|$(-3,5)$
||$y= -3(x-1)^{2}-2$|
向下
|直线$x = 1$
|$(1,-2)$
||$y= 4(x-3)^{2}+7$|
向上
|直线$x = 3$
|$(3,7)$
||$y= -5(x+2)^{2}-6$|
向下
|直线$x = - 2$
|$(-2,-6)$
|
答案:
【解析】:
本题考查二次函数$y = a(x - h)^{2} + k$($a\neq0$)的图象性质,包括开口方向、对称轴和顶点坐标。
对于二次函数的顶点式$y = a(x - h)^{2} + k$($a\neq0$),其性质如下:
开口方向:当$a\gt0$时,抛物线开口向上;当$a\lt0$时,抛物线开口向下。
对称轴:直线$x = h$。
顶点坐标:$(h,k)$。
下面我们根据上述性质分别分析所给的四个二次函数:
函数$y = 2(x + 3)^{2} + 5$:
开口方向:因为$a = 2\gt0$,所以抛物线开口向上。
对称轴:$h = - 3$,所以对称轴为直线$x = - 3$。
顶点坐标:$(h,k)=(-3,5)$。
函数$y = - 3(x - 1)^{2} - 2$:
开口方向:由于$a = - 3\lt0$,抛物线开口向下。
对称轴:$h = 1$,对称轴是直线$x = 1$。
顶点坐标:$(h,k)=(1,-2)$。
函数$y = 4(x - 3)^{2} + 7$:
开口方向:$a = 4\gt0$,抛物线开口向上。
对称轴:$h = 3$,对称轴为直线$x = 3$。
顶点坐标:$(h,k)=(3,7)$。
函数$y = - 5(x + 2)^{2} - 6$:
开口方向:$a = - 5\lt0$,抛物线开口向下。
对称轴:$h = - 2$,对称轴是直线$x = - 2$。
顶点坐标:$(h,k)=(-2,-6)$。
【答案】:
| 二次函数 | 开口方向 | 对称轴 | 顶点坐标 |
| --- | --- | --- | --- |
| $y = 2(x + 3)^{2} + 5$ | 向上 | 直线$x = - 3$ | $(-3,5)$ |
| $y = - 3(x - 1)^{2} - 2$ | 向下 | 直线$x = 1$ | $(1,-2)$ |
| $y = 4(x - 3)^{2} + 7$ | 向上 | 直线$x = 3$ | $(3,7)$ |
| $y = - 5(x + 2)^{2} - 6$ | 向下 | 直线$x = - 2$ | $(-2,-6)$ |
本题考查二次函数$y = a(x - h)^{2} + k$($a\neq0$)的图象性质,包括开口方向、对称轴和顶点坐标。
对于二次函数的顶点式$y = a(x - h)^{2} + k$($a\neq0$),其性质如下:
开口方向:当$a\gt0$时,抛物线开口向上;当$a\lt0$时,抛物线开口向下。
对称轴:直线$x = h$。
顶点坐标:$(h,k)$。
下面我们根据上述性质分别分析所给的四个二次函数:
函数$y = 2(x + 3)^{2} + 5$:
开口方向:因为$a = 2\gt0$,所以抛物线开口向上。
对称轴:$h = - 3$,所以对称轴为直线$x = - 3$。
顶点坐标:$(h,k)=(-3,5)$。
函数$y = - 3(x - 1)^{2} - 2$:
开口方向:由于$a = - 3\lt0$,抛物线开口向下。
对称轴:$h = 1$,对称轴是直线$x = 1$。
顶点坐标:$(h,k)=(1,-2)$。
函数$y = 4(x - 3)^{2} + 7$:
开口方向:$a = 4\gt0$,抛物线开口向上。
对称轴:$h = 3$,对称轴为直线$x = 3$。
顶点坐标:$(h,k)=(3,7)$。
函数$y = - 5(x + 2)^{2} - 6$:
开口方向:$a = - 5\lt0$,抛物线开口向下。
对称轴:$h = - 2$,对称轴是直线$x = - 2$。
顶点坐标:$(h,k)=(-2,-6)$。
【答案】:
| 二次函数 | 开口方向 | 对称轴 | 顶点坐标 |
| --- | --- | --- | --- |
| $y = 2(x + 3)^{2} + 5$ | 向上 | 直线$x = - 3$ | $(-3,5)$ |
| $y = - 3(x - 1)^{2} - 2$ | 向下 | 直线$x = 1$ | $(1,-2)$ |
| $y = 4(x - 3)^{2} + 7$ | 向上 | 直线$x = 3$ | $(3,7)$ |
| $y = - 5(x + 2)^{2} - 6$ | 向下 | 直线$x = - 2$ | $(-2,-6)$ |
2.把下列二次函数化成$y= a(x-h)^{2}+k$的形式.
(1)$y= -3x^{2}+12x-3$;
(2)$y= 4x^{2}-24x+26$;
(3)$y= 2x^{2}+8x-6$;
(4)$y= \frac{1}{2}x^{2}-2x-1$.
(1)$y= -3x^{2}+12x-3$;
$-3(x-2)^{2}+9$
(2)$y= 4x^{2}-24x+26$;
$4(x-3)^{2}-10$
(3)$y= 2x^{2}+8x-6$;
$2(x+2)^{2}-14$
(4)$y= \frac{1}{2}x^{2}-2x-1$.
$\frac{1}{2}(x-2)^{2}-3$
答案:
(1)解:$y=-3x^{2}+12x-3$
$=-3(x^{2}-4x)-3$
$=-3(x^{2}-4x+4-4)-3$
$=-3[(x-2)^{2}-4]-3$
$=-3(x-2)^{2}+12-3$
$=-3(x-2)^{2}+9$
(2)解:$y=4x^{2}-24x+26$
$=4(x^{2}-6x)+26$
$=4(x^{2}-6x+9-9)+26$
$=4[(x-3)^{2}-9]+26$
$=4(x-3)^{2}-36+26$
$=4(x-3)^{2}-10$
(3)解:$y=2x^{2}+8x-6$
$=2(x^{2}+4x)-6$
$=2(x^{2}+4x+4-4)-6$
$=2[(x+2)^{2}-4]-6$
$=2(x+2)^{2}-8-6$
$=2(x+2)^{2}-14$
(4)解:$y=\frac{1}{2}x^{2}-2x-1$
$=\frac{1}{2}(x^{2}-4x)-1$
$=\frac{1}{2}(x^{2}-4x+4-4)-1$
$=\frac{1}{2}[(x-2)^{2}-4]-1$
$=\frac{1}{2}(x-2)^{2}-2-1$
$=\frac{1}{2}(x-2)^{2}-3$
(1)解:$y=-3x^{2}+12x-3$
$=-3(x^{2}-4x)-3$
$=-3(x^{2}-4x+4-4)-3$
$=-3[(x-2)^{2}-4]-3$
$=-3(x-2)^{2}+12-3$
$=-3(x-2)^{2}+9$
(2)解:$y=4x^{2}-24x+26$
$=4(x^{2}-6x)+26$
$=4(x^{2}-6x+9-9)+26$
$=4[(x-3)^{2}-9]+26$
$=4(x-3)^{2}-36+26$
$=4(x-3)^{2}-10$
(3)解:$y=2x^{2}+8x-6$
$=2(x^{2}+4x)-6$
$=2(x^{2}+4x+4-4)-6$
$=2[(x+2)^{2}-4]-6$
$=2(x+2)^{2}-8-6$
$=2(x+2)^{2}-14$
(4)解:$y=\frac{1}{2}x^{2}-2x-1$
$=\frac{1}{2}(x^{2}-4x)-1$
$=\frac{1}{2}(x^{2}-4x+4-4)-1$
$=\frac{1}{2}[(x-2)^{2}-4]-1$
$=\frac{1}{2}(x-2)^{2}-2-1$
$=\frac{1}{2}(x-2)^{2}-3$
3.你能说出二次函数$y= x^{2}-4x+9$的顶点坐标和对称轴吗?
答案:
解:对于二次函数$y = x^2 - 4x + 9$,其中$a = 1$,$b = -4$,$c = 9$。
对称轴为直线$x = -\frac{b}{2a} = -\frac{-4}{2×1} = 2$。
将$x = 2$代入函数,得$y = 2^2 - 4×2 + 9 = 4 - 8 + 9 = 5$。
顶点坐标为$(2, 5)$。
综上,该二次函数的顶点坐标为$(2, 5)$,对称轴为直线$x = 2$。
对称轴为直线$x = -\frac{b}{2a} = -\frac{-4}{2×1} = 2$。
将$x = 2$代入函数,得$y = 2^2 - 4×2 + 9 = 4 - 8 + 9 = 5$。
顶点坐标为$(2, 5)$。
综上,该二次函数的顶点坐标为$(2, 5)$,对称轴为直线$x = 2$。
例1 请你画出二次函数$y= \frac{1}{2}x^{2}-6x+21$的图象.

|x|...|3|4|5|6|7|8|9|...|
|$y= \frac{1}{2}(x-6)^{2}+3$|...| | | | | | | |...|
(思考:表中自变量为什么没有在原点两边对称取?)
描点并画图:(注:自己完成)

注意:画一般式$y= ax^{2}+bx+c$的大致图象时找到顶点、对称轴、与坐标轴的交点即可.
思考:
你能将$y= ax^{2}+bx+c(a≠0)化成y= a(x-h)^{2}+k$的形式吗?试试看.
归纳:
根据$y= ax^{2}+bx+c= a(x+\frac{b}{2a})^{2}+\frac{4ac-b^{2}}{4a}$有下表:
| $y= ax^{2}+bx+c$ | 对称轴 | 顶点坐标 | 最值 | $y随x$的增减性 |
| $a>0$ | 直线$x= -\frac{b}{2a}$ | 最低点$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$ | 最小值$\frac{4ac-b^{2}}{4a}$ | $x>-\frac{b}{2a}$时,$x↑y↑$ $x<-\frac{b}{2a}$时,$x↑y↓$ |
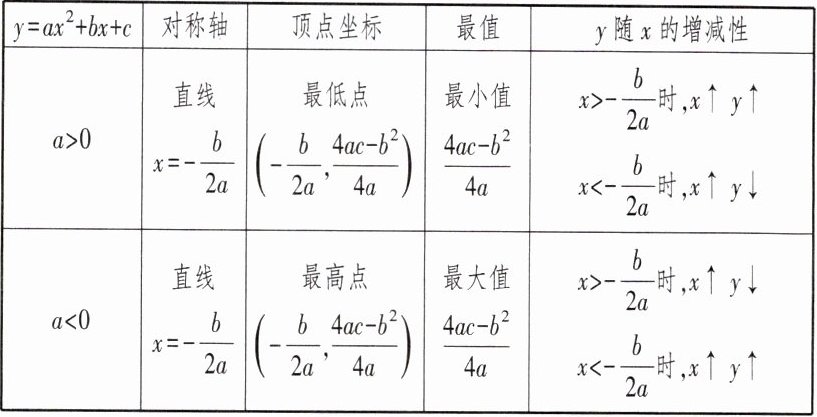
| $a<0$ | 直线$x= -\frac{b}{2a}$ | 最高点$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$ | 最大值$\frac{4ac-b^{2}}{4a}$ | $x>-\frac{b}{2a}$时,$x↑y↓$ $x<-\frac{b}{2a}$时,$x↑y↑$ |
注意:
(1)用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法.
(2)比较函数值的大小,应根据二次函数的对称性把两个点转化在对称轴的同侧,然后利用函数的增减性即可比较大小.或者使用如下结论:若$a>0$,越靠近对称轴$y$值越小;若$a<0$,越靠近对称轴$y$值越大.
试一试:
用公式法写出下列抛物线的对称轴及顶点坐标.
(1)$y= 2x^{2}-3x+4$;(2)$y= -2x^{2}+x+2$;
(3)$y= -x^{2}-4x$.

|x|...|3|4|5|6|7|8|9|...|
|$y= \frac{1}{2}(x-6)^{2}+3$|...| | | | | | | |...|
(思考:表中自变量为什么没有在原点两边对称取?)
描点并画图:(注:自己完成)

注意:画一般式$y= ax^{2}+bx+c$的大致图象时找到顶点、对称轴、与坐标轴的交点即可.
思考:
你能将$y= ax^{2}+bx+c(a≠0)化成y= a(x-h)^{2}+k$的形式吗?试试看.
归纳:
根据$y= ax^{2}+bx+c= a(x+\frac{b}{2a})^{2}+\frac{4ac-b^{2}}{4a}$有下表:
| $y= ax^{2}+bx+c$ | 对称轴 | 顶点坐标 | 最值 | $y随x$的增减性 |
| $a>0$ | 直线$x= -\frac{b}{2a}$ | 最低点$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$ | 最小值$\frac{4ac-b^{2}}{4a}$ | $x>-\frac{b}{2a}$时,$x↑y↑$ $x<-\frac{b}{2a}$时,$x↑y↓$ |

| $a<0$ | 直线$x= -\frac{b}{2a}$ | 最高点$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$ | 最大值$\frac{4ac-b^{2}}{4a}$ | $x>-\frac{b}{2a}$时,$x↑y↓$ $x<-\frac{b}{2a}$时,$x↑y↑$ |
注意:
(1)用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法.
(2)比较函数值的大小,应根据二次函数的对称性把两个点转化在对称轴的同侧,然后利用函数的增减性即可比较大小.或者使用如下结论:若$a>0$,越靠近对称轴$y$值越小;若$a<0$,越靠近对称轴$y$值越大.
试一试:
用公式法写出下列抛物线的对称轴及顶点坐标.
(1)$y= 2x^{2}-3x+4$;(2)$y= -2x^{2}+x+2$;
(3)$y= -x^{2}-4x$.
答案:
【解析】:
本题主要考查二次函数的顶点式、对称轴、顶点坐标以及最值的求解。
对于二次函数$y=ax^{2}+bx+c$,可以通过配方将其转化为顶点式$y=a(x-h)^{2}+k$的形式,其中顶点坐标为$(h,k)$,对称轴为直线$x=h$。
(1)对于函数$y=2x^{2}-3x+4$:
配方得$y=2\left(x-\frac{3}{4}\right)^{2}+\frac{23}{8}$。
所以,对称轴为直线$x=\frac{3}{4}$,顶点坐标为$\left(\frac{3}{4},\frac{23}{8}\right)$。
(2)对于函数$y=-2x^{2}+x+2$:
配方得$y=-2\left(x-\frac{1}{4}\right)^{2}+\frac{17}{8}$。
所以,对称轴为直线$x=\frac{1}{4}$,顶点坐标为$\left(\frac{1}{4},\frac{17}{8}\right)$。
(3)对于函数$y=-x^{2}-4x$:
配方得$y=-(x+2)^{2}+4$。
所以,对称轴为直线$x=-2$,顶点坐标为$(-2,4)$。
【答案】:
(1)对称轴为直线$x=\frac{3}{4}$,顶点坐标为$\left(\frac{3}{4},\frac{23}{8}\right)$;
(2)对称轴为直线$x=\frac{1}{4}$,顶点坐标为$\left(\frac{1}{4},\frac{17}{8}\right)$;
(3)对称轴为直线$x=-2$,顶点坐标为$(-2,4)$。
【解析】:
本题主要考查二次函数的顶点式、对称轴、顶点坐标以及最值的求解。
对于二次函数$y=ax^{2}+bx+c$,可以通过配方将其转化为顶点式$y=a(x-h)^{2}+k$的形式,其中顶点坐标为$(h,k)$,对称轴为直线$x=h$。
(1)对于函数$y=2x^{2}-3x+4$:
配方得$y=2\left(x-\frac{3}{4}\right)^{2}+\frac{23}{8}$。
所以,对称轴为直线$x=\frac{3}{4}$,顶点坐标为$\left(\frac{3}{4},\frac{23}{8}\right)$。
(2)对于函数$y=-2x^{2}+x+2$:
配方得$y=-2\left(x-\frac{1}{4}\right)^{2}+\frac{17}{8}$。
所以,对称轴为直线$x=\frac{1}{4}$,顶点坐标为$\left(\frac{1}{4},\frac{17}{8}\right)$。
(3)对于函数$y=-x^{2}-4x$:
配方得$y=-(x+2)^{2}+4$。
所以,对称轴为直线$x=-2$,顶点坐标为$(-2,4)$。
【答案】:
(1)对称轴为直线$x=\frac{3}{4}$,顶点坐标为$\left(\frac{3}{4},\frac{23}{8}\right)$;
(2)对称轴为直线$x=\frac{1}{4}$,顶点坐标为$\left(\frac{1}{4},\frac{17}{8}\right)$;
(3)对称轴为直线$x=-2$,顶点坐标为$(-2,4)$。

查看更多完整答案,请扫码查看


