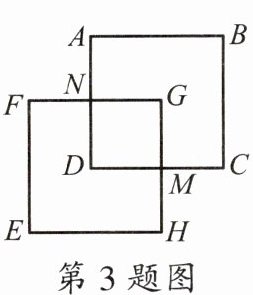
3.如图,若正方形ABCD绕图中某点逆时针旋转90°得到正方形EFGH,则旋转中心应是(
A.点H
B.点N
C.点C
D.点M
D
)
A.点H
B.点N
C.点C
D.点M
答案:
【解析】:本题考查图形旋转的性质及旋转中心的确定方法。
正方形$ABCD$绕某点逆时针旋转$90^{\circ}$得到正方形$EFGH$,需要找到旋转中心。
观察图形,可以发现点$D$旋转后到了点$H$的位置,点$C$旋转后到了点$G$的位置。
由于旋转是$90^{\circ}$,可以推断出旋转中心应当位于连接对应点所成线段的垂直平分线上。
分别作线段$DH$和$CG$的垂直平分线,它们的交点即为旋转中心。
通过作图或逻辑推理,可以确定这个交点是点$M$。
【答案】:D。
正方形$ABCD$绕某点逆时针旋转$90^{\circ}$得到正方形$EFGH$,需要找到旋转中心。
观察图形,可以发现点$D$旋转后到了点$H$的位置,点$C$旋转后到了点$G$的位置。
由于旋转是$90^{\circ}$,可以推断出旋转中心应当位于连接对应点所成线段的垂直平分线上。
分别作线段$DH$和$CG$的垂直平分线,它们的交点即为旋转中心。
通过作图或逻辑推理,可以确定这个交点是点$M$。
【答案】:D。
4.如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点$△A_1B_1C_1,$点A与点$A_1,$点B与点$B_1,$点C与点$C_1$是对应点,则α= ______度.


90
答案:
解:连接AA₁、BB₁,分别作AA₁、BB₁的垂直平分线,两垂直平分线交于点O,点O即为旋转中心。连接OA、OA₁,通过网格计算可得OA=OA₁,且∠AOA₁=90°,故α=90度。
90
90
例3 如图,在△ABC和△ADE中,AB= AC,AD= AE,∠BAC+∠EAD= 180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图1,当∠BAE= 90°时,求证:CD= 2AF.
(2)当∠BAE≠90°时,(1)题中的结论是否成立?请结合图2说明理由.
 分析:(1)因为AF是Rt△ABE的中线,所以BE= 2AF,然后通过△ABE≌△ACD即可求得;(2)延长EA交BC于点G,在AG上截取AH= AD,证△ABH≌△ACD,从而得BH= CD,然后根据三角形的中位线等于底边的一半,求得BH= 2AF,即可得结论.
分析:(1)因为AF是Rt△ABE的中线,所以BE= 2AF,然后通过△ABE≌△ACD即可求得;(2)延长EA交BC于点G,在AG上截取AH= AD,证△ABH≌△ACD,从而得BH= CD,然后根据三角形的中位线等于底边的一半,求得BH= 2AF,即可得结论.
(1)如图1,当∠BAE= 90°时,求证:CD= 2AF.
(2)当∠BAE≠90°时,(1)题中的结论是否成立?请结合图2说明理由.
 分析:(1)因为AF是Rt△ABE的中线,所以BE= 2AF,然后通过△ABE≌△ACD即可求得;(2)延长EA交BC于点G,在AG上截取AH= AD,证△ABH≌△ACD,从而得BH= CD,然后根据三角形的中位线等于底边的一半,求得BH= 2AF,即可得结论.
分析:(1)因为AF是Rt△ABE的中线,所以BE= 2AF,然后通过△ABE≌△ACD即可求得;(2)延长EA交BC于点G,在AG上截取AH= AD,证△ABH≌△ACD,从而得BH= CD,然后根据三角形的中位线等于底边的一半,求得BH= 2AF,即可得结论.
答案:
(1)证明:
∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=180°-∠BAE=90°,
∵F为BE中点,∠BAE=90°,
∴BE=2AF(直角三角形斜边中线等于斜边一半),
在△ABE和△ACD中,
AB=AC,∠BAE=∠CAD=90°,AE=AD,
∴△ABE≌△ACD(SAS),
∴CD=BE,
∴CD=2AF.
(2)解:结论成立.
延长EA至H,使AH=AE,连接BH,
∵F为BE中点,AH=AE,
∴AF是△EBH的中位线,
∴BH=2AF,
∵AD=AE,
∴AH=AD,
∵∠BAC+∠EAD=180°,∠EAD+∠HAD=180°,
∴∠BAC=∠HAD,
∴∠BAC+∠BAH=∠HAD+∠BAH,即∠BAH=∠CAD,
在△ABH和△ACD中,
AB=AC,∠BAH=∠CAD,AH=AD,
∴△ABH≌△ACD(SAS),
∴BH=CD,
∵BH=2AF,
∴CD=2AF.
(1)证明:
∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=180°-∠BAE=90°,
∵F为BE中点,∠BAE=90°,
∴BE=2AF(直角三角形斜边中线等于斜边一半),
在△ABE和△ACD中,
AB=AC,∠BAE=∠CAD=90°,AE=AD,
∴△ABE≌△ACD(SAS),
∴CD=BE,
∴CD=2AF.
(2)解:结论成立.
延长EA至H,使AH=AE,连接BH,
∵F为BE中点,AH=AE,
∴AF是△EBH的中位线,
∴BH=2AF,
∵AD=AE,
∴AH=AD,
∵∠BAC+∠EAD=180°,∠EAD+∠HAD=180°,
∴∠BAC=∠HAD,
∴∠BAC+∠BAH=∠HAD+∠BAH,即∠BAH=∠CAD,
在△ABH和△ACD中,
AB=AC,∠BAH=∠CAD,AH=AD,
∴△ABH≌△ACD(SAS),
∴BH=CD,
∵BH=2AF,
∴CD=2AF.
5.(2024·北京)如图,在菱形ABCD中,∠BAD= 60°,O为对角线的交点.将菱形ABCD绕点O逆时针旋转90°得到菱形A'B'C'D',两个菱形的公共点为E,F,G,H.对八边形BFB'GDHD'E给出下面四个结论:
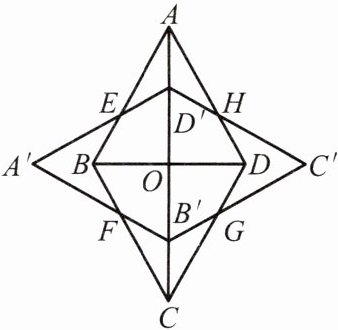
①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是(
A.①③
B.①④
C.②③
D.②④

①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是(
B
)A.①③
B.①④
C.②③
D.②④
答案:
解:设菱形ABCD对角线AC、BD交于O,令OA=1,OB=√3(∠BAD=60°,菱形对角线性质)。
旋转90°后,菱形A'B'C'D'顶点坐标可求(以O为原点建立坐标系)。通过计算各交点E、F、G、H及顶点B、B'、D、D'坐标,得:
① 八边形各边长:通过距离公式计算,所有边长均为√2,相等。
② 各内角:相邻边斜率乘积不同,内角不都相等。
③ 点O到各顶点距离:OB=√3,OE=1,不相等。
④ 点O到各边所在直线距离:由对称性及菱形性质,距离均为√2/2,相等。
正确结论序号:①④
答案:B
旋转90°后,菱形A'B'C'D'顶点坐标可求(以O为原点建立坐标系)。通过计算各交点E、F、G、H及顶点B、B'、D、D'坐标,得:
① 八边形各边长:通过距离公式计算,所有边长均为√2,相等。
② 各内角:相邻边斜率乘积不同,内角不都相等。
③ 点O到各顶点距离:OB=√3,OE=1,不相等。
④ 点O到各边所在直线距离:由对称性及菱形性质,距离均为√2/2,相等。
正确结论序号:①④
答案:B
1.中心对称的定义:把一个图形绕着某一个点旋转
180°
,如果它能够与另一个图形重合
,那么就说这两个图形关于这个点对称
或中心对称
,这个点叫做对称中心
.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点
.
答案:
180°;重合;关于这个点对称;中心对称;对称中心;对称点
2.中心对称的性质.
(1)在成中心对称的两个图形中,对称点所连线段都经过
(2)关于中心对称的两个图形是
(3)关于中心对称的两个图形,对应线段
3.对比中心对称与轴对称.
| 轴对称 | 中心对称 |
| --- | --- |
| 有至少一条对称轴——直线 | 有一个对称中心——点 |
| 图形沿对称轴对折(翻折180°)后重合 | 图形绕对称中心旋转180°后重合 |
| 折叠后与另一图形重合 | 旋转后与另一图形重合 |
| 对称点的连线被对称轴垂直平分 | 对称点连线经过对称中心,且被对称中心平分 |
(1)在成中心对称的两个图形中,对称点所连线段都经过
对称中心
,而且被对称中心平分
;(2)关于中心对称的两个图形是
全等
图形;(3)关于中心对称的两个图形,对应线段
平行
(或在同一直线上)且相等
.3.对比中心对称与轴对称.
| 轴对称 | 中心对称 |
| --- | --- |
| 有至少一条对称轴——直线 | 有一个对称中心——点 |
| 图形沿对称轴对折(翻折180°)后重合 | 图形绕对称中心旋转180°后重合 |
| 折叠后与另一图形重合 | 旋转后与另一图形重合 |
| 对称点的连线被对称轴垂直平分 | 对称点连线经过对称中心,且被对称中心平分 |
答案:
【解析】:
本题主要考察了中心对称的性质以及中心对称与轴对称的对比。
对于中心对称的性质部分:
(1) 在成中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心平分。这是中心对称的基本性质。
(2) 关于中心对称的两个图形是全等图形,因为两个图形可以通过旋转180度完全重合。
(3) 关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
对于中心对称与轴对称的对比部分:
表格中详细列出了轴对称和中心对称的不同特点,包括对称轴或对称中心、图形变换方式以及对称点的连线性质等。
【答案】:
(1) 在成中心对称的两个图形中,对称点所连线段都经过对称中心,而且被对称中心平分;
(2) 关于中心对称的两个图形是全等图形;
(3) 关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
本题主要考察了中心对称的性质以及中心对称与轴对称的对比。
对于中心对称的性质部分:
(1) 在成中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心平分。这是中心对称的基本性质。
(2) 关于中心对称的两个图形是全等图形,因为两个图形可以通过旋转180度完全重合。
(3) 关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
对于中心对称与轴对称的对比部分:
表格中详细列出了轴对称和中心对称的不同特点,包括对称轴或对称中心、图形变换方式以及对称点的连线性质等。
【答案】:
(1) 在成中心对称的两个图形中,对称点所连线段都经过对称中心,而且被对称中心平分;
(2) 关于中心对称的两个图形是全等图形;
(3) 关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3.对比中心对称与轴对称.
| 轴对称 | 中心对称 |
| --- | --- |
| 有至少一条对称轴——直线 | 有一个对称中心——点 |
| 图形沿对称轴对折(翻折180°)后重合 | 图形绕对称中心旋转180°后重合 |
| 折叠后与另一图形重合 | 旋转后与另一图形重合 |
| 对称点的连线被对称轴垂直平分 | 对称点连线经过对称中心,且被对称中心平分 |
| 轴对称 | 中心对称 |
| --- | --- |
| 有至少一条对称轴——直线 | 有一个对称中心——点 |
| 图形沿对称轴对折(翻折180°)后重合 | 图形绕对称中心旋转180°后重合 |
| 折叠后与另一图形重合 | 旋转后与另一图形重合 |
| 对称点的连线被对称轴垂直平分 | 对称点连线经过对称中心,且被对称中心平分 |
答案:
【解析】:
本题要求对比中心对称与轴对称的性质和特点。题目已经给出了轴对称和中心对称的基本定义和性质,包括对称轴、对称中心、对称操作(翻折或旋转)以及对称点的连线性质。我们需要根据这些信息,对两者进行对比分析。
轴对称是指图形关于某条直线(对称轴)对称,即图形上的每一点关于对称轴都有对称点,且这两点与对称轴的距离相等,连线被对称轴垂直平分。
中心对称是指图形关于某一点(对称中心)对称,即图形上的每一点关于对称中心都有对称点,且这两点与对称中心的连线在同一直线上,但方向相反,连线被对称中心平分。
【答案】:
轴对称与中心对称的对比:
轴对称:
对称轴:至少有一条对称轴,为直线。
对称操作:图形沿对称轴对折(翻折$180^\circ$)后重合。
对称点连线:对称点的连线被对称轴垂直平分。
中心对称:
对称中心:有一个对称中心,为点。
对称操作:图形绕对称中心旋转$180^\circ$后重合。
对称点连线:对称点连线经过对称中心,且被对称中心平分。
本题要求对比中心对称与轴对称的性质和特点。题目已经给出了轴对称和中心对称的基本定义和性质,包括对称轴、对称中心、对称操作(翻折或旋转)以及对称点的连线性质。我们需要根据这些信息,对两者进行对比分析。
轴对称是指图形关于某条直线(对称轴)对称,即图形上的每一点关于对称轴都有对称点,且这两点与对称轴的距离相等,连线被对称轴垂直平分。
中心对称是指图形关于某一点(对称中心)对称,即图形上的每一点关于对称中心都有对称点,且这两点与对称中心的连线在同一直线上,但方向相反,连线被对称中心平分。
【答案】:
轴对称与中心对称的对比:
轴对称:
对称轴:至少有一条对称轴,为直线。
对称操作:图形沿对称轴对折(翻折$180^\circ$)后重合。
对称点连线:对称点的连线被对称轴垂直平分。
中心对称:
对称中心:有一个对称中心,为点。
对称操作:图形绕对称中心旋转$180^\circ$后重合。
对称点连线:对称点连线经过对称中心,且被对称中心平分。
查看更多完整答案,请扫码查看


