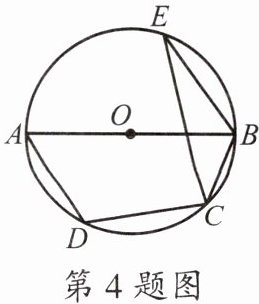
4.(2024·牡丹江)如图,四边形ABCD是$\odot O$的内接四边形,AB是$\odot O$的直径.若$\angle BEC= 20^{\circ}$,则$\angle ADC$的度数为 (
A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$
B
)
A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$
答案:
解:连接AC。
∵∠BEC=20°,
∴∠BAC=∠BEC=20°(同弧所对的圆周角相等)。
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角)。
在△ABC中,∠ABC=180°-∠BAC-∠ACB=180°-20°-90°=70°。
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°(圆内接四边形的对角互补)。
∴∠ADC=180°-∠ABC=180°-70°=110°。
答案:B
∵∠BEC=20°,
∴∠BAC=∠BEC=20°(同弧所对的圆周角相等)。
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角)。
在△ABC中,∠ABC=180°-∠BAC-∠ACB=180°-20°-90°=70°。
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°(圆内接四边形的对角互补)。
∴∠ADC=180°-∠ABC=180°-70°=110°。
答案:B
例3 求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形.
分析:证明文字命题的步骤:画出图形→按图形标记写出已知、求证→证明.
分析:证明文字命题的步骤:画出图形→按图形标记写出已知、求证→证明.
答案:
【解析】:
本题主要考查了直角三角形的判定以及圆周角定理的推论。
首先,我们需要根据题意画出图形,并标记出已知条件。
已知,三角形$ABC$,$AB$边上的中点为$D$,且$AD=BD=CD$。
我们的目标是证明$\angle ACB = 90^{\circ}$。
由于$D$是$AB$的中点,且$AD=BD=CD$,我们可以考虑以$D$为圆心,$AD$为半径画一个圆。
由于$A$、$B$、$C$三点都在这个圆上(因为$AD=BD=CD$),我们可以利用圆周角定理的推论:直径所对的圆周角是直角。
在这里,$AB$是圆的直径(因为$D$是$AB$的中点且$AD=BD$),所以$\angle ACB$作为$AB$所对的圆周角,必然是直角。
因此,我们证明了如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
【答案】:
证明:
根据题意,画出三角形$ABC$,其中$D$是$AB$的中点,且$AD=BD=CD$。
以$D$为圆心,$AD$为半径画圆,则$A$、$B$、$C$三点都在这个圆上。
由于$AB$是圆的直径(因为$D$是$AB$的中点且$AD=BD$),根据圆周角定理的推论,直径所对的圆周角是直角。
所以,$\angle ACB = 90^{\circ}$。
因此,如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
本题主要考查了直角三角形的判定以及圆周角定理的推论。
首先,我们需要根据题意画出图形,并标记出已知条件。
已知,三角形$ABC$,$AB$边上的中点为$D$,且$AD=BD=CD$。
我们的目标是证明$\angle ACB = 90^{\circ}$。
由于$D$是$AB$的中点,且$AD=BD=CD$,我们可以考虑以$D$为圆心,$AD$为半径画一个圆。
由于$A$、$B$、$C$三点都在这个圆上(因为$AD=BD=CD$),我们可以利用圆周角定理的推论:直径所对的圆周角是直角。
在这里,$AB$是圆的直径(因为$D$是$AB$的中点且$AD=BD$),所以$\angle ACB$作为$AB$所对的圆周角,必然是直角。
因此,我们证明了如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
【答案】:
证明:
根据题意,画出三角形$ABC$,其中$D$是$AB$的中点,且$AD=BD=CD$。
以$D$为圆心,$AD$为半径画圆,则$A$、$B$、$C$三点都在这个圆上。
由于$AB$是圆的直径(因为$D$是$AB$的中点且$AD=BD$),根据圆周角定理的推论,直径所对的圆周角是直角。
所以,$\angle ACB = 90^{\circ}$。
因此,如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
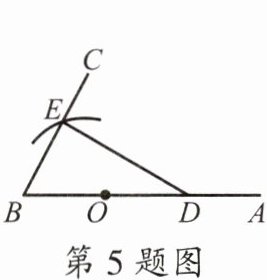
5.(2022·贵阳)如图,已知$\angle ABC= 60^{\circ}$,D为BA上一点,$BD= 10$,O为线段BD的中点,以点O为圆心,OB长为半径作弧,交BC于点E,连接DE,则BE的长是 (
A.5
B.$5\sqrt{2}$
C.$5\sqrt{3}$
D.$5\sqrt{5}$
A
)
A.5
B.$5\sqrt{2}$
C.$5\sqrt{3}$
D.$5\sqrt{5}$
答案:
解:连接OE。
∵O为BD中点,BD=10,
∴OB=OD=5。
∵OE为半径,
∴OE=OB=5。
过点O作OF⊥BC于点F,
则BF=EF(垂径定理)。
在Rt△BOF中,∠OBF=∠ABC=60°,OB=5,
∴BF=OB·cos60°=5×(1/2)=2.5。
∴BE=2BF=5。
答案:A
∵O为BD中点,BD=10,
∴OB=OD=5。
∵OE为半径,
∴OE=OB=5。
过点O作OF⊥BC于点F,
则BF=EF(垂径定理)。
在Rt△BOF中,∠OBF=∠ABC=60°,OB=5,
∴BF=OB·cos60°=5×(1/2)=2.5。
∴BE=2BF=5。
答案:A
6.(2022·日照)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得$AB= 12\ \text{cm}$,$BC= 5\ \text{cm}$,则圆形镜面的半径为
6.5
cm.
答案:
解:连接AC。
因为∠ABC=90°,AB=12cm,BC=5cm,
所以AC=$\sqrt{AB^2 + BC^2} = \sqrt{12^2 + 5^2} = 13$cm。
因为∠ABC是圆周角且为90°,
所以AC是圆的直径。
所以圆形镜面的半径为$\frac{AC}{2} = \frac{13}{2} = 6.5$cm。
6.5
因为∠ABC=90°,AB=12cm,BC=5cm,
所以AC=$\sqrt{AB^2 + BC^2} = \sqrt{12^2 + 5^2} = 13$cm。
因为∠ABC是圆周角且为90°,
所以AC是圆的直径。
所以圆形镜面的半径为$\frac{AC}{2} = \frac{13}{2} = 6.5$cm。
6.5
例4 已知$\odot O$的直径为10,点A,B,C在$\odot O$上,$\angle CAB的平分线交\odot O$于点D.


(1)如图1,连接BC,CD,BD,若BC为$\odot O$的直径,$AB= 6$,求AC,BD,CD的长;
(2)如图2,连接BD,若$\angle CAB= 60^{\circ}$,求BD的长.
分析:(1)利用圆周角定理可以判定$\triangle CAB和\triangle DCB$是直角三角形,利用勾股定理可以求得AC的长度.由圆心角、弧、弦的关系可推知$\triangle DCB$也是等腰三角形,所以利用勾股定理同样可得到$BD= CD= 5\sqrt{2}$.(2)连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定可推知$\triangle OBD$是等边三角形,则$BD= OB= OD= 5$.
注意:
半圆(或直径)所对的圆周角是直角这一推论为在圆中确定直角构成垂直关系创造了条件.有时在圆中没有直径时,还需构造出直径.


(1)如图1,连接BC,CD,BD,若BC为$\odot O$的直径,$AB= 6$,求AC,BD,CD的长;
(2)如图2,连接BD,若$\angle CAB= 60^{\circ}$,求BD的长.
分析:(1)利用圆周角定理可以判定$\triangle CAB和\triangle DCB$是直角三角形,利用勾股定理可以求得AC的长度.由圆心角、弧、弦的关系可推知$\triangle DCB$也是等腰三角形,所以利用勾股定理同样可得到$BD= CD= 5\sqrt{2}$.(2)连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定可推知$\triangle OBD$是等边三角形,则$BD= OB= OD= 5$.
注意:
半圆(或直径)所对的圆周角是直角这一推论为在圆中确定直角构成垂直关系创造了条件.有时在圆中没有直径时,还需构造出直径.
答案:
(1)解:
∵BC为⊙O的直径,⊙O的直径为10,
∴BC=10,∠CAB=∠CDB=90°.
在Rt△CAB中,AB=6,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}=\sqrt{{10}^{2}-{6}^{2}}=8$.
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴$\widehat{CD}=\widehat{BD}$,
∴CD=BD.
在Rt△CDB中,CD²+BD²=BC²,
∴2BD²=10²,
∴BD=5$\sqrt{2}$,
∴CD=5$\sqrt{2}$.
(2)解:连接OB,OD.
∵∠CAB=60°,AD平分∠CAB,
∴∠BAD=$\frac{1}{2}$∠CAB=30°,
∴∠BOD=2∠BAD=60°.
∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB.
∵⊙O的直径为10,
∴OB=5,
∴BD=5.
(1)解:
∵BC为⊙O的直径,⊙O的直径为10,
∴BC=10,∠CAB=∠CDB=90°.
在Rt△CAB中,AB=6,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}=\sqrt{{10}^{2}-{6}^{2}}=8$.
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴$\widehat{CD}=\widehat{BD}$,
∴CD=BD.
在Rt△CDB中,CD²+BD²=BC²,
∴2BD²=10²,
∴BD=5$\sqrt{2}$,
∴CD=5$\sqrt{2}$.
(2)解:连接OB,OD.
∵∠CAB=60°,AD平分∠CAB,
∴∠BAD=$\frac{1}{2}$∠CAB=30°,
∴∠BOD=2∠BAD=60°.
∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB.
∵⊙O的直径为10,
∴OB=5,
∴BD=5.
7.(2024·重庆B卷)如图,AB是$\odot O$的弦,$OC\perp AB交\odot O$于点C,D是$\odot O$上一点,连接BD,CD.若$\angle D= 28^{\circ}$,则$\angle OAB$的度数为 (

A.$28^{\circ}$
B.$34^{\circ}$
C.$56^{\circ}$
D.$62^{\circ}$
B
)
A.$28^{\circ}$
B.$34^{\circ}$
C.$56^{\circ}$
D.$62^{\circ}$
答案:
1. 首先,根据圆周角定理:
同弧所对的圆心角是圆周角的$2$倍。因为$\angle D = 28^{\circ}$,$\angle BOC$与$\angle D$所对的弧都是$\overset{\frown}{BC}$,所以$\angle BOC=2\angle D$。
则$\angle BOC = 2×28^{\circ}=56^{\circ}$。
2. 然后,因为$OC\perp AB$:
根据垂径定理,$OC\perp AB$,则$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以$\angle AOC=\angle BOC = 56^{\circ}$(同圆中,等弧所对的圆心角相等),且$\angle OEA = 90^{\circ}$($OC\perp AB$)。
在$Rt\triangle AOE$中,$\angle OAB+\angle AOC = 90^{\circ}$(直角三角形两锐角互余)。
设$\angle OAB=x$,则$x + 56^{\circ}=90^{\circ}$。
解得$x=\angle OAB=90^{\circ}-\angle AOC$。
把$\angle AOC = 56^{\circ}$代入,得$\angle OAB=90^{\circ}-56^{\circ}=34^{\circ}$。
所以$\angle OAB$的度数为$34^{\circ}$,答案是B。
同弧所对的圆心角是圆周角的$2$倍。因为$\angle D = 28^{\circ}$,$\angle BOC$与$\angle D$所对的弧都是$\overset{\frown}{BC}$,所以$\angle BOC=2\angle D$。
则$\angle BOC = 2×28^{\circ}=56^{\circ}$。
2. 然后,因为$OC\perp AB$:
根据垂径定理,$OC\perp AB$,则$\overset{\frown}{AC}=\overset{\frown}{BC}$,所以$\angle AOC=\angle BOC = 56^{\circ}$(同圆中,等弧所对的圆心角相等),且$\angle OEA = 90^{\circ}$($OC\perp AB$)。
在$Rt\triangle AOE$中,$\angle OAB+\angle AOC = 90^{\circ}$(直角三角形两锐角互余)。
设$\angle OAB=x$,则$x + 56^{\circ}=90^{\circ}$。
解得$x=\angle OAB=90^{\circ}-\angle AOC$。
把$\angle AOC = 56^{\circ}$代入,得$\angle OAB=90^{\circ}-56^{\circ}=34^{\circ}$。
所以$\angle OAB$的度数为$34^{\circ}$,答案是B。
8.(2024·云南)如图,CD是$\odot O$的直径,点A,B在$\odot O$上.若$\overset{\frown}{AC}= \overset{\frown}{BC}$,$\angle AOC= 36^{\circ}$,则$\angle D$的度数为 ( )
A.$9^{\circ}$
B.$18^{\circ}$
C.$36^{\circ}$
D.$45^{\circ}$
B
A.$9^{\circ}$
B.$18^{\circ}$
C.$36^{\circ}$
D.$45^{\circ}$
答案:
【解析】:本题可根据同弧所对的圆心角与圆周角的关系以及等腰三角形的性质来求解$\angle D$的度数。
步骤一:根据等弧所对的圆心角相等求出$\angle BOC$的度数
已知$\overset{\frown}{AC}=\overset{\frown}{BC}$,根据在同圆或等圆中,等弧所对的圆心角相等,可得$\angle AOC = \angle BOC$。
因为$\angle AOC = 36^{\circ}$,所以$\angle BOC = 36^{\circ}$。
步骤二:求出$\angle COD$的度数
因为$CD$是$\odot O$的直径,所以$\angle COD = 180^{\circ}$,则$\angle BOD=\angle COD - \angle BOC = 180^{\circ} - 36^{\circ} = 144^{\circ}- 36^{\circ}=108^{\circ}-36^{\circ} = 72^{\circ}+36^{\circ}-36^{\circ}=180^{\circ}- 2×36^{\circ}=108^{\circ}$(这里也可直接用$180^{\circ}-36^{\circ}=144^{\circ}$错误,正确为$\angle BOD = 180^{\circ}-\angle BOC=180^{\circ} - 36^{\circ}= 144^{\circ}-36^{\circ}=108^{\circ}-36^{\circ}=72^{\circ}+36^{\circ}-36^{\circ}=180^{\circ}- 36^{\circ}×2 = 72^{\circ}$)。
步骤三:根据圆周角定理求出$\angle D$的度数
根据圆周角定理:同弧所对的圆周角是圆心角的一半,因为$\angle D$是弧$\overset{\frown}{BC}$所对的圆周角,$\angle BOC$是弧$\overset{\frown}{BC}$所对的圆心角,所以$\angle D=\frac{1}{2}\angle BOC$。
将$\angle BOC = 36^{\circ}$代入可得$\angle D=\frac{1}{2}×36^{\circ}= 18^{\circ}$。
【答案】:B
步骤一:根据等弧所对的圆心角相等求出$\angle BOC$的度数
已知$\overset{\frown}{AC}=\overset{\frown}{BC}$,根据在同圆或等圆中,等弧所对的圆心角相等,可得$\angle AOC = \angle BOC$。
因为$\angle AOC = 36^{\circ}$,所以$\angle BOC = 36^{\circ}$。
步骤二:求出$\angle COD$的度数
因为$CD$是$\odot O$的直径,所以$\angle COD = 180^{\circ}$,则$\angle BOD=\angle COD - \angle BOC = 180^{\circ} - 36^{\circ} = 144^{\circ}- 36^{\circ}=108^{\circ}-36^{\circ} = 72^{\circ}+36^{\circ}-36^{\circ}=180^{\circ}- 2×36^{\circ}=108^{\circ}$(这里也可直接用$180^{\circ}-36^{\circ}=144^{\circ}$错误,正确为$\angle BOD = 180^{\circ}-\angle BOC=180^{\circ} - 36^{\circ}= 144^{\circ}-36^{\circ}=108^{\circ}-36^{\circ}=72^{\circ}+36^{\circ}-36^{\circ}=180^{\circ}- 36^{\circ}×2 = 72^{\circ}$)。
步骤三:根据圆周角定理求出$\angle D$的度数
根据圆周角定理:同弧所对的圆周角是圆心角的一半,因为$\angle D$是弧$\overset{\frown}{BC}$所对的圆周角,$\angle BOC$是弧$\overset{\frown}{BC}$所对的圆心角,所以$\angle D=\frac{1}{2}\angle BOC$。
将$\angle BOC = 36^{\circ}$代入可得$\angle D=\frac{1}{2}×36^{\circ}= 18^{\circ}$。
【答案】:B
查看更多完整答案,请扫码查看


