《2025年巅峰对决九年级数学上册人教版》

3. 从地面竖直向上抛出一小球,小球的高度h(m)与小球运动时间t(s)之间的函数关系如图所示.下列结论:①小球抛出3 s时达到最高点;②小球从抛出到落地经过的路程是80 m;③小球的高度h= 20时,t= 1或t= 5;④小球抛出2 s后的高度是35 m.其中正确的有( )A


A.①②
B.②③
C.①③④
D.①②③

答案： 解：①由图像可知，抛物线顶点横坐标为3，即小球抛出3s时达到最高点，正确。
②小球从抛出到落地经过的路程是上升40m加下降40m，共80m，正确。
③设抛物线解析式为$h=a(t-3)^2 + 40$，将$(0,0)$代入得$0 = a(0 - 3)^2 + 40$，解得$a=-\frac{40}{9}$，所以$h=-\frac{40}{9}(t - 3)^2 + 40$。当$h = 20$时，$20=-\frac{40}{9}(t - 3)^2 + 40$，$\frac{40}{9}(t - 3)^2=20$，$(t - 3)^2=\frac{9}{2}$，$t=3\pm\frac{3\sqrt{2}}{2}\neq1$或$5$，错误。
④当$t = 2$时，$h=-\frac{40}{9}(2 - 3)^2 + 40=-\frac{40}{9}+40=\frac{320}{9}\approx35.56\neq35$，错误。
综上，正确的是①②，选A。
答案：A

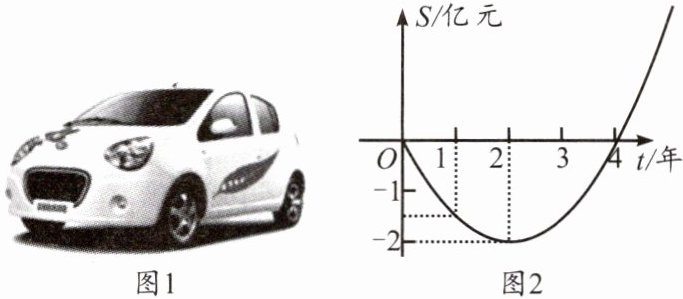
4. 如图1所示是某企业投入市场的一种高效环保型新能源电动车示意图,企业经历了从投入到盈利过程,如图2的二次函数的图象描述了该企业年初以来累积利润S(亿元)与销售时间t(年)之间的关系[即前t(年)的利润总和S与t之间的关系].则截止到第______年末企业累积利润可达到30亿元.

10

答案： 解：由图2可知二次函数顶点坐标为(2,-2)，设其解析式为$S=a(t-2)^2-2$。
将点(0,0)代入解析式得：$0=a(0-2)^2-2$，即$4a-2=0$，解得$a=\frac{1}{2}$。
所以二次函数解析式为$S=\frac{1}{2}(t-2)^2-2$。
当$S=30$时，$\frac{1}{2}(t-2)^2-2=30$，
$\frac{1}{2}(t-2)^2=32$，
$(t-2)^2=64$，
$t-2=\pm8$，
解得$t_1=10$，$t_2=-6$（舍去）。
故截止到第10年末企业累积利润可达到30亿元。
答案：10

1. 函数$y= ax^{2}(a≠0)$的图象是一条抛物线,它的顶点坐标是$(0,0)$,对称轴是$y$轴（或 $x = 0$）,当$a$$＞$0时,开口向上;当$a$$＜$0时,开口向下.

答案： 【解析】：
本题考查二次函数$y = ax^{2}$（$a \neq 0$）的基本性质，包括图象形状、顶点坐标、对称轴以及开口方向与系数$a$的关系。
对于函数$y = ax^{2}$（$a \neq 0$）：
1. 其图象是一条抛物线。这是因为二次函数的图象总是抛物线。
2. 顶点坐标是$(0,0)$。对于一般形式的二次函数$y = ax^{2} + bx + c$，顶点坐标为$(-\frac{b}{2a}, c - \frac{b^{2}}{4a})$。但在本题中，$b = 0$，$c = 0$，所以顶点坐标为$(0,0)$。
3. 对称轴是$y$轴，即$x = 0$。对于一般形式的二次函数，对称轴为$x = -\frac{b}{2a}$。在本题中，由于$b = 0$，对称轴为$x = 0$，即$y$轴。
4. 当$a ＞ 0$时，抛物线开口向上；当$a ＜ 0$时，抛物线开口向下。这是因为二次函数的开口方向由系数$a$决定。
【答案】：
抛物线；$(0,0)$；$y$轴（或 $x = 0$）；$＞$；$＜$

2. 抛物线$y= \frac{1}{4}x^{2}$的顶点坐标是$(0,0)$,对称轴是$y$轴（或 $x=0$）,开口向上;抛物线$y= -3x^{2}$的顶点坐标是$(0,0)$,对称轴是$y$轴（或 $x=0$）,开口向下.

答案： 【解析】：
本题主要考察二次函数抛物线的基本性质，包括顶点坐标，对称轴，以及开口方向。
对于抛物线$y=ax^{2}+bx+c$，其顶点坐标为$(-\frac{b}{2a},c-\frac{b^{2}}{4a})$，对称轴为$x=-\frac{b}{2a}$。
对于开口方向，当$a＞0$时，开口向上；当$a＜0$时，开口向下。
对于抛物线$y= \frac{1}{4}x^{2}$，其形式为$y=ax^{2}$，其中$a=\frac{1}{4}$，$b=0$，$c=0$。
所以，顶点坐标为$(0,0)$，对称轴为$x=0$（即y轴），且因为$a＞0$，所以开口向上。
对于抛物线$y= -3x^{2}$，其形式同样为$y=ax^{2}$，其中$a=-3$，$b=0$，$c=0$。
所以，顶点坐标为$(0,0)$，对称轴为$x=0$（即y轴），且因为$a＜0$，所以开口向下。
【答案】：
$(0,0)$；$y$轴（或 $x=0$）；上；$(0,0)$；$y$轴（或 $x=0$）；下。

例1 抛物线形拱桥的剖面图如图所示,当拱顶离水面2 m时,水面宽4 m.若水面下降1 m,则水面宽度将增加多少米?

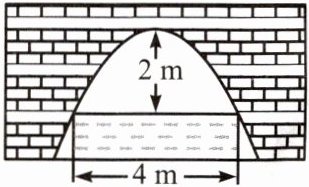
分析:因为桥拱是抛物线,故可建立合适的平面直角坐标系,为了简洁,可选择抛物线顶点为原点,对称轴为y轴建立平面直角坐标系,找出抛物线的解析式,则易于计算.

答案： 【解析】：本题考查了二次函数在实际问题中的应用，通过建立平面直角坐标系，求出抛物线的解析式，再根据水面下降的情况计算出新的水面宽度，进而求出水面宽度增加的值。
以抛物线的顶点为原点，对称轴为$y$轴建立平面直角坐标系。
设抛物线的解析式为$y = ax^2$（$a\neq0$）。
已知当拱顶离水面$2m$时，水面宽$4m$，即当$y = - 2$时，$x = \pm2$，把$x = 2$，$y = - 2$代入$y = ax^2$，可得$-2=a×2^2$，解得$a=-\frac{1}{2}$。
所以抛物线的解析式为$y = -\frac{1}{2}x^2$。
当水面下降$1m$时，此时$y = - 3$，把$y = - 3$代入$y = -\frac{1}{2}x^2$，可得$-3=-\frac{1}{2}x^2$，即$x^2 = 6$，解得$x = \pm\sqrt{6}$。
那么此时水面宽度为$2\sqrt{6}m$。
原来水面宽$4m$，则水面宽度增加了$(2\sqrt{6}-4)m$。
【答案】：水面宽度将增加$(2\sqrt{6}-4)$米。

1.(2022·广安)如图所示是抛物线形拱桥,当拱顶离水面2 m时,水面宽6 m,当水面下降$\frac{14}{9}$m时,水面宽8 m.

答案： 解：以拱顶为原点，竖直向下为y轴正方向，建立平面直角坐标系。
设抛物线解析式为$y = ax^2$。
当拱顶离水面2m时，水面宽6m，此时水面上一点坐标为$(3, 2)$，代入解析式得$2 = a×3^2$，解得$a=\frac{2}{9}$，故抛物线解析式为$y=\frac{2}{9}x^2$。
当水面宽8m时，此时水面上一点的横坐标为$4$，代入解析式得$y=\frac{2}{9}×4^2=\frac{32}{9}$。
水面下降高度为$\frac{32}{9}-2=\frac{14}{9}$m。
$\frac{14}{9}$

2."卢沟晓月"是著名的北京八景之一,每当黎明斜月西沉,月色倒影水中,更显明媚皎洁.古时乾隆皇帝曾在秋日路过卢沟桥,赋诗"半钩留照三秋淡,一练分波平镜明"于此,并题"卢沟晓月",立碑于桥头.卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度OA约为22 m,若按如图所示方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为$y= -\frac{13}{121}(x-11)^{2}+k$,则主桥拱最高点P与其在水中倒影$P'$之间的距离为______m.

26

答案： 【解析】：本题考查二次函数在实际问题中的应用。
首先，根据题目，桥拱在水面的跨度$OA$约为$22m$，
因此点$A$的坐标为$(22, 0)$。
主桥拱所在抛物线可以表示为：$y= -\frac{13}{121}(x-11)^{2}+k$，
将点$A(22, 0)$的坐标代入抛物线方程，
得到$0= -\frac{13}{121}(22-11)^{2}+k$，
化简可得：$0= -\frac{13}{121}× 11^{2}+k$，
$0= -\frac{13}{121}× 121+k$，
$0= -13+k$，
解得：$k= 13$。
因此，抛物线的解析式为$y= -\frac{13}{121}(x-11)^{2}+13$，
由于抛物线的顶点式$y= a(x-h)^{2}+k$中，顶点坐标为$(h, k)$，
所以此抛物线的顶点$P$的坐标为$(11, 13)$。
由于点$P$关于$x$轴的对称点$P'$的纵坐标是$P$点纵坐标的相反数，
所以$P'$的坐标为$(11, -13)$。
最后，求$P$和$P'$之间的距离，即两点间纵坐标之差的绝对值，
为$|13-(-13)|=26(m)$。
【答案】：$26$。

例2 如图,排球运动员站在点O处练习发球,将球从点O正上方2 m的点A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足解析式$y= a(x-6)^{2}+h$.已知球网与点O的水平距离为9 m,高度为2.43 m,球场的边界距点O的水平距离为18 m.
(1)当$h= 2.6$时,求y与x的解析式.(不要求写出自变量x的取值范围)
(2)当$h= 2.6$时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界,求h的取值范围.

分析:(1)根据函数图象上的点的坐标满足函数解析式,把$x= 0,y= 2及h= 2.6代入y= a(x-6)^{2}+h$中即可求出函数解析式;(2)根据函数解析式确定函数图象上点的坐标,并解决相关问题;(3)先把$x= 0,y= 2代入y= a(x-6)^{2}+h中求出a= \frac{2-h}{36}$,然后分别表示出$x= 9,x= 18$时,y的值应满足的条件,解之即可.

答案： 【解析】：
(1)根据题目，排球的运行高度$y$与运行的水平距离$x$满足解析式 $y = a(x - 6)^{2} + h$。
已知当 $x = 0$ 时，$y = 2$（球从点A处发出，高度为2m），且 $h = 2.6$。
将这些值代入解析式，得到：
$2 = a(0 - 6)^{2} + 2.6$，
$2 = 36a + 2.6$，
解这个方程，得到：
$36a = 2 - 2.6$，
$36a = -0.6$，
$a = -\frac{1}{60}$。
因此，$y$ 与 $x$ 的解析式为：
$y = -\frac{1}{60}(x - 6)^{2} + 2.6$。
(2)当 $h = 2.6$ 时，需要判断球是否能越过球网以及是否会出界。
球网与点 $O$ 的水平距离为 9m，高度为 2.43m。
将 $x = 9$ 代入解析式 $y = -\frac{1}{60}(x - 6)^{2} + 2.6$，得到：
$y = -\frac{1}{60}(9 - 6)^{2} + 2.6$，
$y = -\frac{1}{60} × 9 + 2.6$，
$y = -\frac{9}{60} + 2.6$，
$y = 2.45$，
由于 $2.45 ＞ 2.43$，所以球能越过球网。
接下来，判断球是否会出界。
球场的边界距点 $O$ 的水平距离为 18m。
将$x = 18$ 代入解析式，得到：
$y = -\frac{1}{60}(18 - 6)^{2} + 2.6$，
$y = -\frac{1}{60} × 144 + 2.6$，
$y = -2.4 + 2.6$，
$y = 0.2$，
由于 $y = 0.2 ＞ 0$，说明球在到达球场边界时仍然在空中，因此球会出界。
(3)若球一定能越过球网，又不出边界，需要求出 $h$ 的取值范围。
首先，将 $x = 0, y = 2$ 代入解析式 $y = a(x - 6)^{2} + h$，得到：
$2 = 36a + h$，
$a = \frac{2 - h}{36}$，
然后，将 $a$ 的值代入解析式，得到新的解析式：
$y = \frac{2 - h}{36}(x - 6)^{2} + h$，
当 $x = 9$ 时，$y$ 的值应大于 2.43（球网高度），即：
$\frac{2 - h}{36}(9 - 6)^{2} + h ＞ 2.43$，
解这个不等式，得到 $h ＞ \frac{83}{50}$。
当 $x = 18$ 时，$y$ 的值应小于等于 0（球场边界），即：
$\frac{2 - h}{36}(18 - 6)^{2} + h \leq 0$，
解这个不等式，得到 $h \geq \frac{8}{3}$。
综合以上两个不等式，得到 $h$ 的取值范围为 $h \geq \frac{8}{3}$。
【答案】：
(1) $y = -\frac{1}{60}(x - 6)^{2} + 2.6$；
(2) 球能越过球网，因为当 $x = 9$ 时，$y = 2.45 ＞ 2.43$；球会出界，因为当 $x = 18$ 时，$y = 0.2 ＞ 0$；
(3) $h$ 的取值范围是 $h \geq \frac{8}{3}$。