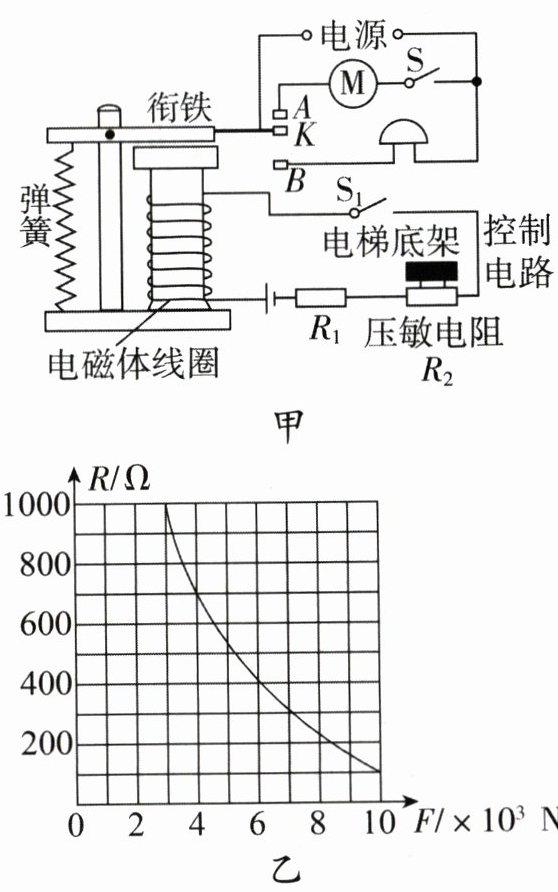
19. (10 分)电梯为居民的出入带来很大的便利,出于安全考虑,电梯都设置了超载自动报警系统,其工作原理如图甲所示。系统电路由工作电路和控制电路组成:当电梯没有超载时,工作电路中的动触点 K 与静触点 A 接触,闭合开关 S,电动机正常工作;当电梯超载时,工作电路中的动触点 K 与静触点 B 接触,电铃发出报警铃声,即使闭合开关 S,电动机也不工作。当控制电路中的电磁铁线圈中的电流达到 20mA 时,动触点 K 刚好接触静触点 B,电铃发出警报声。已知电梯自重为 3×10³N,控制电路中的电源电压 U = 6V,保护电阻 R₁ = 200Ω,压敏电阻 R₂的阻值随压力 F 大小变化如图乙所示。若 g 取 10N/kg,电磁铁线圈的阻值忽略不计。求:
(1)该电梯的最大载重质量;
(2)电梯空载时,通过电磁铁线圈的电流大小。
(1)该电梯的最大载重质量;
(2)电梯空载时,通过电磁铁线圈的电流大小。

答案:
解:
(1) 由 $I = \frac{U}{R}$ 得,当电磁铁线圈中的电流达到 20 mA 时,控制电路的总电阻
$R_{总}=\frac{U_{总}}{I_{总}}=\frac{6\ V}{0.02\ A}=300\ \Omega$
压敏电阻的阻值
$R_{2}=R_{总}-R_{1}=300\ \Omega - 200\ \Omega = 100\ \Omega$
由图乙可知,此时压敏电阻所受的压力为 $F_{1}=1.0\times10^{4}\ N$,电梯的最大载重为
$G = F_{1}-G_{自重}=1.0\times10^{4}\ N - 3\times10^{3}\ N = 7\times10^{3}\ N$
质量为
$m = \frac{G}{g}=\frac{7\times10^{3}\ N}{10\ N/kg}=7\times10^{2}\ kg$
(2) 由题图乙可知,当压敏电阻所受的压力 $F_{2}=3\times10^{3}\ N$ 时,压敏电阻的阻值 $R_{2}' = 1000\ \Omega$,
$R_{总}' = R_{2}'+R_{1}=1000\ \Omega + 200\ \Omega = 1200\ \Omega$,
通过电磁铁线圈的电流大小
$I'=\frac{U_{总}}{R_{总}'}=\frac{6\ V}{1200\ \Omega}=0.005\ A$
答:
(1) 该电梯的最大载重质量是 $7\times10^{2}\ kg$;
(2) 电梯空载时,通过电磁铁线圈的电流大小是 0.005 A。
(1) 由 $I = \frac{U}{R}$ 得,当电磁铁线圈中的电流达到 20 mA 时,控制电路的总电阻
$R_{总}=\frac{U_{总}}{I_{总}}=\frac{6\ V}{0.02\ A}=300\ \Omega$
压敏电阻的阻值
$R_{2}=R_{总}-R_{1}=300\ \Omega - 200\ \Omega = 100\ \Omega$
由图乙可知,此时压敏电阻所受的压力为 $F_{1}=1.0\times10^{4}\ N$,电梯的最大载重为
$G = F_{1}-G_{自重}=1.0\times10^{4}\ N - 3\times10^{3}\ N = 7\times10^{3}\ N$
质量为
$m = \frac{G}{g}=\frac{7\times10^{3}\ N}{10\ N/kg}=7\times10^{2}\ kg$
(2) 由题图乙可知,当压敏电阻所受的压力 $F_{2}=3\times10^{3}\ N$ 时,压敏电阻的阻值 $R_{2}' = 1000\ \Omega$,
$R_{总}' = R_{2}'+R_{1}=1000\ \Omega + 200\ \Omega = 1200\ \Omega$,
通过电磁铁线圈的电流大小
$I'=\frac{U_{总}}{R_{总}'}=\frac{6\ V}{1200\ \Omega}=0.005\ A$
答:
(1) 该电梯的最大载重质量是 $7\times10^{2}\ kg$;
(2) 电梯空载时,通过电磁铁线圈的电流大小是 0.005 A。
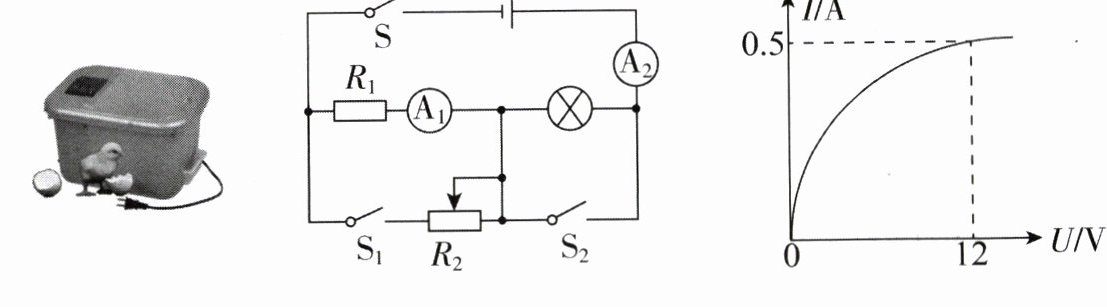
20. (12 分)如图是一种小鸡孵化器,其电路如图所示,在一般情况下,只需灯光照明,灯泡的额定电压为 12V,温度较低时,则需要加热,电源电压为 72V,R₁为定值电阻,R₂为阻值可变的发热电阻丝(标有“200Ω 3A”的字样),电流表 A₁的量程为 0 ~ 0.6A,电流表 A₂的量程为 0 ~ 3A,通过灯泡的电流与灯泡两端的电压关系如图所示,仅闭合 S 时,灯泡恰好正常发光,求:
(1)灯泡正常发光时的电阻值 Rₗ;
(2)R₁的阻值;
(3)S、S₁、S₂均闭合时,电路安全的情况下 R₂消耗电功率的最小值和最大值。
(1)灯泡正常发光时的电阻值 Rₗ;
(2)R₁的阻值;
(3)S、S₁、S₂均闭合时,电路安全的情况下 R₂消耗电功率的最小值和最大值。

答案:
解:
(1) 灯泡额定电压为 12 V,根据 $I - U$ 图象可知,12 V 时的电流为 0.5 A,根据欧姆定律得,灯泡正常发光时的电阻值 $R_{L}$ 为
$R_{L}=\frac{U_{额}}{I_{L}}=\frac{12\ V}{0.5\ A}=24\ \Omega$
(2) 仅闭合 $S$ 时,灯泡恰好正常发光,由图知,灯与 $R_{1}$ 串联,电流相等,即
$I = I_{L}=0.5\ A$
$R_{1}$ 的阻值为
$R_{1}=\frac{U - U_{额}}{I}=\frac{72\ V - 12\ V}{0.5\ A}=120\ \Omega$
(3) 如图,$S$、$S_{1}$、$S_{2}$ 均闭合时,灯被短路,$R_{1}$ 与 $R_{2}$ 并联,电流表 $A_{1}$ 测量 $R_{1}$ 的电流,电流表 $A_{2}$ 测量干路电流;当滑动变阻器阻值最大时,功率最小,则最小功率为
$P_{最小}=\frac{U^{2}}{R_{大}}=\frac{(72\ V)^{2}}{200\ \Omega}=25.92\ W$
通过 $R_{1}$ 的电流为
$I_{1}=\frac{U}{R_{1}}=\frac{72\ V}{120\ \Omega}=0.6\ A$
电流表 $A_{1}$ 测量干路电流,根据其量程得 $R_{2}$ 的最大电流为
$I_{2}=3\ A - 0.6\ A = 2.4\ A$
此时 $R_{2}$ 的功率最大,最大功率为
$P_{最大}=UI_{2}=72\ V\times2.4\ A = 172.8\ W$
答:
(1) 灯泡正常发光时的电阻值 $R_{L}$ 为 24 $\Omega$;
(2) $R_{1}$ 的阻值为 120 $\Omega$;
(3) $S$、$S_{1}$、$S_{2}$ 均闭合时,电路安全的情况下 $R_{2}$ 消耗电功率的最小值和最大值分别为 25.92 W 和 172.8 W。
(1) 灯泡额定电压为 12 V,根据 $I - U$ 图象可知,12 V 时的电流为 0.5 A,根据欧姆定律得,灯泡正常发光时的电阻值 $R_{L}$ 为
$R_{L}=\frac{U_{额}}{I_{L}}=\frac{12\ V}{0.5\ A}=24\ \Omega$
(2) 仅闭合 $S$ 时,灯泡恰好正常发光,由图知,灯与 $R_{1}$ 串联,电流相等,即
$I = I_{L}=0.5\ A$
$R_{1}$ 的阻值为
$R_{1}=\frac{U - U_{额}}{I}=\frac{72\ V - 12\ V}{0.5\ A}=120\ \Omega$
(3) 如图,$S$、$S_{1}$、$S_{2}$ 均闭合时,灯被短路,$R_{1}$ 与 $R_{2}$ 并联,电流表 $A_{1}$ 测量 $R_{1}$ 的电流,电流表 $A_{2}$ 测量干路电流;当滑动变阻器阻值最大时,功率最小,则最小功率为
$P_{最小}=\frac{U^{2}}{R_{大}}=\frac{(72\ V)^{2}}{200\ \Omega}=25.92\ W$
通过 $R_{1}$ 的电流为
$I_{1}=\frac{U}{R_{1}}=\frac{72\ V}{120\ \Omega}=0.6\ A$
电流表 $A_{1}$ 测量干路电流,根据其量程得 $R_{2}$ 的最大电流为
$I_{2}=3\ A - 0.6\ A = 2.4\ A$
此时 $R_{2}$ 的功率最大,最大功率为
$P_{最大}=UI_{2}=72\ V\times2.4\ A = 172.8\ W$
答:
(1) 灯泡正常发光时的电阻值 $R_{L}$ 为 24 $\Omega$;
(2) $R_{1}$ 的阻值为 120 $\Omega$;
(3) $S$、$S_{1}$、$S_{2}$ 均闭合时,电路安全的情况下 $R_{2}$ 消耗电功率的最小值和最大值分别为 25.92 W 和 172.8 W。
查看更多完整答案,请扫码查看


