2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
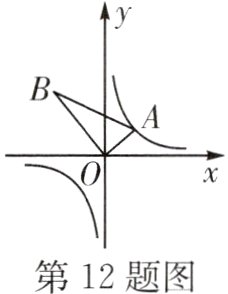
12. 如图,$\triangle AOB$是直角三角形,$\angle AOB = 90^{\circ}$,$OB = 2OA$,点$A$在反比例函数$y=\frac{1}{x}$的图象上.若点$B$在反比例函数$y=\frac{k}{x}$的图象上,则$k$的值为______.

答案:
-4
13. 如图,将三角形纸片$ABC$按如图所示的方式折叠,使点$B$落在边$AC$上,记为点$B'$,折痕为$EF$,已知$AB = 3$,$AC = 4$,$BC = 5$.若以$B'$,$F$,$C$为顶点的三角形与$\triangle ABC$相似,则$CF$的长是____________.


答案:
$\frac{25}{8}$ 或 $\frac{20}{7}$
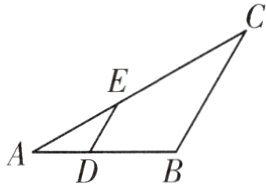
14. (8分)如图,$D$,$E$分别是$AB$,$AC$上的点,$\triangle ADE\sim\triangle ABC$,相似比是$\frac{2}{5}$,$DE = 4\ cm$,$\angle C = 30^{\circ}$,求$BC$,$\angle AED$.

答案:
解:$\because\triangle ADE\sim\triangle ABC$,$\therefore\angle AED=\angle C = 30^{\circ}$,$\frac{DE}{BC}=\frac{2}{5}$。
$\because DE = 4\text{ cm}$,$\therefore BC = 10\text{ cm}$。
$\because DE = 4\text{ cm}$,$\therefore BC = 10\text{ cm}$。
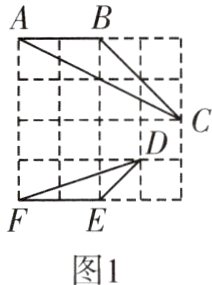
15. (12分)(1)判断图1、图2中的两个三角形是否相似;
(2)求图2中$x$和$y$的值.

(2)求图2中$x$和$y$的值.


答案:
解:
(1)图1:设小正方形的边长为1,则$AB = 2$,
$BC=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$AC=\sqrt{2^{2}+4^{2}} = 2\sqrt{5}$,
$EF = 2$,$DE=\sqrt{1^{2}+1^{2}}=\sqrt{2}$,$DF=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
$\therefore\frac{BC}{EF}=\frac{AB}{DE}=\frac{AC}{DF}=\sqrt{2}$。
$\therefore\triangle ABC\sim\triangle DEF$。
图2:$\because\frac{CD}{CB}=\frac{CE}{CA}=\frac{26}{39}=\frac{40}{60}=\frac{2}{3}$,$\angle ACB=\angle ECD$,
$\therefore\triangle ABC\sim\triangle EDC$。
(2)$\because\triangle ABC\sim\triangle EDC$,$\therefore\angle B=\angle D = 98^{\circ}$,即$y = 98$。
$\because\frac{DE}{BA}=\frac{CD}{CB}$,即$\frac{27}{x}=\frac{26}{39}$,解得$x = 40.5$。
(1)图1:设小正方形的边长为1,则$AB = 2$,
$BC=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$AC=\sqrt{2^{2}+4^{2}} = 2\sqrt{5}$,
$EF = 2$,$DE=\sqrt{1^{2}+1^{2}}=\sqrt{2}$,$DF=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,
$\therefore\frac{BC}{EF}=\frac{AB}{DE}=\frac{AC}{DF}=\sqrt{2}$。
$\therefore\triangle ABC\sim\triangle DEF$。
图2:$\because\frac{CD}{CB}=\frac{CE}{CA}=\frac{26}{39}=\frac{40}{60}=\frac{2}{3}$,$\angle ACB=\angle ECD$,
$\therefore\triangle ABC\sim\triangle EDC$。
(2)$\because\triangle ABC\sim\triangle EDC$,$\therefore\angle B=\angle D = 98^{\circ}$,即$y = 98$。
$\because\frac{DE}{BA}=\frac{CD}{CB}$,即$\frac{27}{x}=\frac{26}{39}$,解得$x = 40.5$。
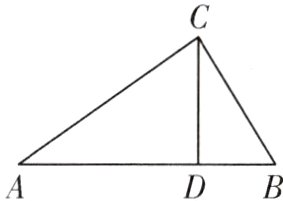
16. (13分)如图,在$\triangle ABC$中,$CD$是边$AB$上的高,且$\frac{AD}{CD}=\frac{CD}{BD}$.
(1)求证:$\triangle ACD\sim\triangle CBD$;
(2)求$\angle ACB$的度数.
(1)求证:$\triangle ACD\sim\triangle CBD$;
(2)求$\angle ACB$的度数.

答案:
(1)证明:$\because CD$是边$AB$上的高,
$\therefore\angle ADC=\angle CDB = 90^{\circ}$。
$\because\frac{AD}{CD}=\frac{CD}{BD}$,$\therefore\triangle ACD\sim\triangle CBD$。
(2)解:$\because\triangle ACD\sim\triangle CBD$,
$\therefore\angle A=\angle BCD$。
在$\triangle ACD$中,$\angle ADC = 90^{\circ}$,
$\therefore\angle A+\angle ACD = 90^{\circ}$。
$\therefore\angle BCD+\angle ACD = 90^{\circ}$,
即$\angle ACB = 90^{\circ}$。
(1)证明:$\because CD$是边$AB$上的高,
$\therefore\angle ADC=\angle CDB = 90^{\circ}$。
$\because\frac{AD}{CD}=\frac{CD}{BD}$,$\therefore\triangle ACD\sim\triangle CBD$。
(2)解:$\because\triangle ACD\sim\triangle CBD$,
$\therefore\angle A=\angle BCD$。
在$\triangle ACD$中,$\angle ADC = 90^{\circ}$,
$\therefore\angle A+\angle ACD = 90^{\circ}$。
$\therefore\angle BCD+\angle ACD = 90^{\circ}$,
即$\angle ACB = 90^{\circ}$。
17. (15分)如图,在$\triangle ABC$中,以$AB$为直径作$\odot O$,交边$AC$于点$E$,交边$BC$于点$D$,连接$DE$,$AD$,$BE$,$AD$与$BE$相交于点$F$.
(1)求证:$\triangle CDE\sim\triangle CAB$;
(2)若$EF = 2$,$AF = BF = 6$,求$CE$的长.
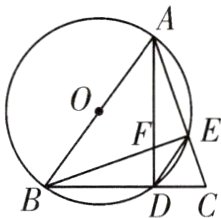
(1)求证:$\triangle CDE\sim\triangle CAB$;
(2)若$EF = 2$,$AF = BF = 6$,求$CE$的长.
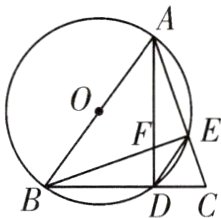
答案:
(1)证明:$\because\angle ABC+\angle AED = 180^{\circ}$,$\angle AED+\angle DEC = 180^{\circ}$,
$\therefore\angle ABC=\angle DEC$。
又$\because\angle C=\angle C$,
$\therefore\triangle CDE\sim\triangle CAB$。
(2)解:$\because\angle BAD=\angle BED$,$\angle ABE=\angle ADE$,
$\therefore\triangle DEF\sim\triangle BAF$。
$\therefore\frac{DE}{BA}=\frac{EF}{AF}=\frac{2}{6}=\frac{1}{3}$。
$\because\triangle CDE\sim\triangle CAB$,$\therefore\frac{DE}{AB}=\frac{CE}{CB}=\frac{1}{3}$。
设$CE = x$,则$CB = 3x$,
$\because AB$为$\odot O$的直径,
$\therefore\angle AEB = 90^{\circ}$。$\therefore\angle BEC = 90^{\circ}$。
$\because EF = 2$,$BF = 6$,$\therefore BE = 8$。
在$Rt\triangle BEC$中,$BE^{2}+CE^{2}=BC^{2}$,即$8^{2}+x^{2}=(3x)^{2}$,
解得$x_{1}=2\sqrt{2}$,$x_{2}=-2\sqrt{2}$(舍去)。
$\therefore CE$的长为$2\sqrt{2}$。
(1)证明:$\because\angle ABC+\angle AED = 180^{\circ}$,$\angle AED+\angle DEC = 180^{\circ}$,
$\therefore\angle ABC=\angle DEC$。
又$\because\angle C=\angle C$,
$\therefore\triangle CDE\sim\triangle CAB$。
(2)解:$\because\angle BAD=\angle BED$,$\angle ABE=\angle ADE$,
$\therefore\triangle DEF\sim\triangle BAF$。
$\therefore\frac{DE}{BA}=\frac{EF}{AF}=\frac{2}{6}=\frac{1}{3}$。
$\because\triangle CDE\sim\triangle CAB$,$\therefore\frac{DE}{AB}=\frac{CE}{CB}=\frac{1}{3}$。
设$CE = x$,则$CB = 3x$,
$\because AB$为$\odot O$的直径,
$\therefore\angle AEB = 90^{\circ}$。$\therefore\angle BEC = 90^{\circ}$。
$\because EF = 2$,$BF = 6$,$\therefore BE = 8$。
在$Rt\triangle BEC$中,$BE^{2}+CE^{2}=BC^{2}$,即$8^{2}+x^{2}=(3x)^{2}$,
解得$x_{1}=2\sqrt{2}$,$x_{2}=-2\sqrt{2}$(舍去)。
$\therefore CE$的长为$2\sqrt{2}$。
查看更多完整答案,请扫码查看


