《2025年畅行课堂九年级数学下册人教版山西专版》

13. (10分)已知反比例函数$y = \frac{k}{x}(k \neq 0)$的图象的一支如图所示，它经过点$B(-3,2)$.

(1)求这个反比例函数的解析式，并补画这个反比例函数图象的另一支；
(2)当$y \leq 4$，且$y \neq 0$时，求自变量x的取值范围.

答案： 解:
(1)把点$B(-3,2)$代入$y = \frac{k}{x}(k\neq0)$，得$2 = \frac{k}{-3}$，解得$k = -6$.
$\therefore$反比例函数的解析式为$y = -\frac{6}{x}$.补画这个反比例函数图象的另一支略.
(2)当$y = 4$时，$-\frac{6}{x} = 4$，解得$x = -\frac{3}{2}$.
$\therefore$当$y\leq4$，且$y\neq0$时，$x\leq -\frac{3}{2}$或$x＞0$.

14. (12分)已知$y = y_{1} - y_{2}$，$y_{1}$与x成反比例，$y_{2}$与$x - 2$成正比例，且当$x = 1$时，$y = -1$；当$x = 3$时，$y = 5$. 求当$x = 5$时，y的值.

答案： 解:$\because y_1$与$x$成反比例，$y_2$与$x - 2$成正比例，
$\therefore$设$y_1 = \frac{m}{x}(m\neq0)$，$y_2 = k(x - 2)(k\neq0)$.
$\because y = y_1 - y_2$，$\therefore y = \frac{m}{x} - k(x - 2)$.
$\because$当$x = 1$时，$y = -1$；当$x = 3$时，$y = 5$，
$\therefore\begin{cases}m + k = -1\\\frac{m}{3} - k = 5\end{cases}$，解得$\begin{cases}m = 3\\k = -4\end{cases}$.
$\therefore y = \frac{3}{x} + 4x - 8$.
$\therefore$当$x = 5$时，$y = \frac{63}{5}$.

15. (14分)如图，已知反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象经过点$A(2,-2)$，$AB \perp y$轴于点B，C为y轴正半轴上一点，连接AC.
(1)求反比例函数的解析式；
(2)请用无刻度的直尺和圆规，在x轴正半轴上找一点D，使得$\angle OBD = \angle BAC$（要求：不写作法，保留作图痕迹）；
(3)在(2)的条件下，求证：$AC = BD$.

答案：

(1)解:$\because$反比例函数$y = \frac{k}{x}(x＞0)$的图象经过点$A(2,-2)$，
$\therefore -2 = \frac{k}{2}$，解得$k = -4$.
$\therefore$反比例函数的解析式为$y = -\frac{4}{x}$.
(2)解:如图所示，点$D$即为所求.
(3)证明:$\because$点$A(2,-2)$，$AB\perp y$轴于点$B$，
$\therefore AB = OB = 2$.
$\because\angle BOD = \angle ABC = 90^{\circ}$，$\angle OBD = \angle BAC$，
$\therefore\triangle ABC\cong\triangle BOD(ASA)$.$\therefore AC = BD$.

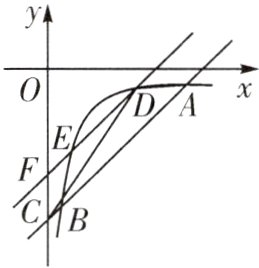
16. (16分)如图，已知一次函数$y_{1} = kx + b$的图象与反比例函数$y_{2} = \frac{m}{x}(x ＞ 0)$的图象交于$A(6,-\frac{1}{2})$，$B(\frac{1}{2},n)$两点，与y轴交于点C. 将直线AB沿y轴向上平移t个单位长度得到直线DE. DE与y轴交于点F，交$y_{2} = \frac{m}{x}(x ＞ 0)$的图象于点D.
(1)求$y_{1}$与$y_{2}$的解析式；
(2)观察图象，直接写出$y_{1} ＜ y_{2}$时x的取值范围；
(3)连接AD，CD，若$\triangle ACD$的面积为6，求t的值.

答案：
解:
(1)将点$A(6,-\frac{1}{2})$代入$y_2 = \frac{m}{x}(x＞0)$，得$-\frac{1}{2} = \frac{m}{6}$，解得$m = -3$.
$\therefore$反比例函数的解析式为$y_2 = -\frac{3}{x}$.
$\because$点$B(\frac{1}{2},n)$在$y_2 = -\frac{3}{x}$的图象上，
$\therefore n = -6$.$\therefore B(\frac{1}{2},-6)$.
将点$A(6,-\frac{1}{2})$，$B(\frac{1}{2},-6)$代入$y_1 = kx + b$，得$\begin{cases}6k + b = -\frac{1}{2}\\\frac{1}{2}k + b = -6\end{cases}$，解得$\begin{cases}k = 1\\b = -\frac{13}{2}\end{cases}$.
$\therefore$一次函数的解析式为$y_1 = x - \frac{13}{2}$.
(2)当$y_1 ＜ y_2$时，$x$的取值范围是$\frac{1}{2} ＜ x ＜ 6$.
(3)如图，连接$AF$.
$\because$直线$AB$沿$y$轴向上平移$t$个单位长度得到直线$DE$，
$\therefore CF = t$.
$\because AB// DF$，$\therefore S_{\triangle ACD} = S_{\triangle ACF}$.
$\therefore\frac{1}{2}CF\cdot|x_A| = 6$，即$\frac{1}{2}\times6t = 6$.
解得$t = 2$.