搜索
2025年畅行课堂九年级数学下册人教版山西专版
注：目前有些书本章节名称可能整理的还不是很完善，但都是按照顺序排列的，请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的，请勿直接抄袭。
9. 如图,在□ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F.若△DEF的面积为9,则△DAF的面积为______.
答案：
12
10. 如图,在边长为1的正方形网格中,点A,B,C,D,E均为格点,则∠ADB + ∠AEB=______.
答案：
45°
11. 如图,在△ABC中,AD是中线,点E在AD上,且CE=CD=1,∠BAD=∠ACE,则AC的长为______.
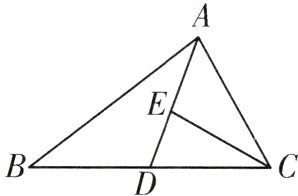
答案：
$\sqrt{2}$
三、解答题(共45分)
12. (14分)如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)以原点为位似中心,在原点的另一侧画出△A₁B₁C₁,使$\frac{AB}{A₁B₁}=\frac{1}{2}$;
(2)写出△A₁B₁C₁各顶点的坐标.
12. (14分)如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)以原点为位似中心,在原点的另一侧画出△A₁B₁C₁,使$\frac{AB}{A₁B₁}=\frac{1}{2}$;
(2)写出△A₁B₁C₁各顶点的坐标.
答案：
解：
(1)如图所示，$\triangle A_{1}B_{1}C_{1}$即为所求.
(2)$A_{1}(-2,-6)$，$B_{1}(-8,-4)$，$C_{1}(-4,-2)$.
解：
(1)如图所示，$\triangle A_{1}B_{1}C_{1}$即为所求.
(2)$A_{1}(-2,-6)$，$B_{1}(-8,-4)$，$C_{1}(-4,-2)$.
13. (15分)如图,在△ABC和△ADE中,∠BAC=∠DAE = 90°,∠B = ∠ADE = 30°,AC与DE相交于点F,连接CE,点D在边BC上.
(1)求证:△ABD∽△ACE;
(2)若$\frac{AD}{BD}=\sqrt{3}$,求$\frac{DF}{CF}$的值.
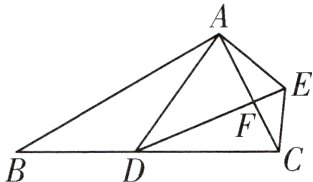
(1)求证:△ABD∽△ACE;
(2)若$\frac{AD}{BD}=\sqrt{3}$,求$\frac{DF}{CF}$的值.
答案：
(1)证明：$\because\angle BAC=\angle DAE$，$\angle B=\angle ADE$，$\therefore\triangle BAC\sim\triangle DAE$.$\therefore\frac{BA}{DA}=\frac{AC}{AE}$，即$\frac{BA}{AC}=\frac{DA}{AE}$.$\because\angle BAC=\angle DAE$，$\therefore\angle BAD=\angle CAE$.$\therefore\triangle ABD\sim\triangle ACE$.
(2)解：$\because\triangle ABD\sim\triangle ACE$，$\therefore\frac{AD}{AE}=\frac{BD}{CE}$，$\angle B=\angle ACE=\angle ADE$.$\therefore\frac{AD}{BD}=\frac{AE}{EC}=\sqrt{3}$.$\because\angle DAE = 90^{\circ}$，$\angle ADE = 30^{\circ}$，$\therefore\frac{AD}{AE}=\sqrt{3}$.$\therefore\frac{AD}{EC}=\frac{AD}{AE}\cdot\frac{AE}{EC}=\sqrt{3}\times\sqrt{3}=3$.$\because\angle ADE=\angle ACE$，$\angle AFD=\angle EFC$$\therefore\triangle ADF\sim\triangle ECF$，$\therefore\frac{DF}{CF}=\frac{AD}{EC}=3$.
(1)证明：$\because\angle BAC=\angle DAE$，$\angle B=\angle ADE$，$\therefore\triangle BAC\sim\triangle DAE$.$\therefore\frac{BA}{DA}=\frac{AC}{AE}$，即$\frac{BA}{AC}=\frac{DA}{AE}$.$\because\angle BAC=\angle DAE$，$\therefore\angle BAD=\angle CAE$.$\therefore\triangle ABD\sim\triangle ACE$.
(2)解：$\because\triangle ABD\sim\triangle ACE$，$\therefore\frac{AD}{AE}=\frac{BD}{CE}$，$\angle B=\angle ACE=\angle ADE$.$\therefore\frac{AD}{BD}=\frac{AE}{EC}=\sqrt{3}$.$\because\angle DAE = 90^{\circ}$，$\angle ADE = 30^{\circ}$，$\therefore\frac{AD}{AE}=\sqrt{3}$.$\therefore\frac{AD}{EC}=\frac{AD}{AE}\cdot\frac{AE}{EC}=\sqrt{3}\times\sqrt{3}=3$.$\because\angle ADE=\angle ACE$，$\angle AFD=\angle EFC$$\therefore\triangle ADF\sim\triangle ECF$，$\therefore\frac{DF}{CF}=\frac{AD}{EC}=3$.
14. (16分)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC²=CE·CA.
(1)求证:BC=CD;
(2)分别延长AB,DC相交于点P,若PB=OB,CD=2$\sqrt{2}$,求⊙O的半径.
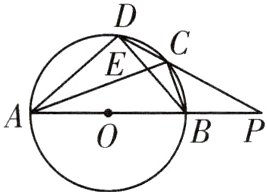
(1)求证:BC=CD;
(2)分别延长AB,DC相交于点P,若PB=OB,CD=2$\sqrt{2}$,求⊙O的半径.
答案：
(1)证明：$\because DC^{2}=CE\cdot CA$，$\therefore\frac{DC}{CE}=\frac{CA}{DC}$.又$\because\angle ACD=\angle DCE$，$\therefore\triangle CAD\sim\triangle CDE$.$\therefore\angle CAD=\angle CDE$.$\because\angle CAD=\angle CBD$，$\therefore\angle CDB=\angle CBD$.$\therefore BC = DC$.
(2)解：如图，连接$OC$，设$\odot O$的半径为$r$，
$\because CD = CB$，$\therefore\overset{\frown}{CD}=\overset{\frown}{CB}$.$\therefore\angle DAC=\angle BAC$.$\therefore\angle BOC=\angle BAD$.$\therefore OC// AD$.又$\because PB = OB$，$\therefore\frac{PC}{CD}=\frac{PO}{OA}=\frac{2r}{r}=2$.$\therefore PC = 2CD = 4\sqrt{2}$.$\because\angle PCB=\angle PAD$，$\angle CPB=\angle APD$$\therefore\triangle PCB\sim\triangle PAD$.$\therefore\frac{PC}{PA}=\frac{PB}{PD}$，即$\frac{4\sqrt{2}}{3r}=\frac{r}{6\sqrt{2}}$，解得$r = 4$(负值舍去).$\therefore\odot O$的半径为4.
(1)证明：$\because DC^{2}=CE\cdot CA$，$\therefore\frac{DC}{CE}=\frac{CA}{DC}$.又$\because\angle ACD=\angle DCE$，$\therefore\triangle CAD\sim\triangle CDE$.$\therefore\angle CAD=\angle CDE$.$\because\angle CAD=\angle CBD$，$\therefore\angle CDB=\angle CBD$.$\therefore BC = DC$.
(2)解：如图，连接$OC$，设$\odot O$的半径为$r$，
$\because CD = CB$，$\therefore\overset{\frown}{CD}=\overset{\frown}{CB}$.$\therefore\angle DAC=\angle BAC$.$\therefore\angle BOC=\angle BAD$.$\therefore OC// AD$.又$\because PB = OB$，$\therefore\frac{PC}{CD}=\frac{PO}{OA}=\frac{2r}{r}=2$.$\therefore PC = 2CD = 4\sqrt{2}$.$\because\angle PCB=\angle PAD$，$\angle CPB=\angle APD$$\therefore\triangle PCB\sim\triangle PAD$.$\therefore\frac{PC}{PA}=\frac{PB}{PD}$，即$\frac{4\sqrt{2}}{3r}=\frac{r}{6\sqrt{2}}$，解得$r = 4$(负值舍去).$\therefore\odot O$的半径为4. 查看更多完整答案，请扫码查看
