第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 伽利略理想斜面实验如图所示,小球沿斜面由静止滚下,再滚上另一斜面。

(1) 在实际生活中,小球滚上另一斜面的最大高度等于h吗?
(2) 设想斜面是光滑的,小球滚上另一斜面的最大高度等于h吗?
(3) 设想斜面是光滑的,若减小第二个斜面的倾角,小球还能滚到另一斜面高h处吗?与没减小斜面倾角之前相比,小球滚到另一斜面高h处通过的路程如何变化?
(4) 设想第二个斜面变成水平面,这时小球试图滚上另一斜面的相同高度,但永远达不到。这时小球的运动能停下来吗?

(1) 在实际生活中,小球滚上另一斜面的最大高度等于h吗?
(2) 设想斜面是光滑的,小球滚上另一斜面的最大高度等于h吗?
(3) 设想斜面是光滑的,若减小第二个斜面的倾角,小球还能滚到另一斜面高h处吗?与没减小斜面倾角之前相比,小球滚到另一斜面高h处通过的路程如何变化?
(4) 设想第二个斜面变成水平面,这时小球试图滚上另一斜面的相同高度,但永远达不到。这时小球的运动能停下来吗?
答案:
提示:
(1)不等于。
(2)等于h。
(3)能,通过的路程变大。
(4)不能,永远运动下去。
(1)不等于。
(2)等于h。
(3)能,通过的路程变大。
(4)不能,永远运动下去。
2. 伽利略理想斜面实验说明力________(选填“是”或“不是”)维持物体运动的原因。
答案:
不是
3. 伽利略理想斜面实验运用的方法:在________基础上进一步________。
答案:
实验 推理
[微训练]
根据预习内容判断以下说法正误。
1. 亚里士多德认为力是维持物体运动的原因。( )
2. 笛卡儿认为物体的运动状态不需要力来维持。( )
3. 伽利略的理想实验说明了力是维持物体运动的原因。( )
根据预习内容判断以下说法正误。
1. 亚里士多德认为力是维持物体运动的原因。( )
2. 笛卡儿认为物体的运动状态不需要力来维持。( )
3. 伽利略的理想实验说明了力是维持物体运动的原因。( )
答案:
√
@@√
@@×
@@√
@@×
1. 牛顿第一定律揭示了运动和力的关系:力不是__________物体运动状态的原因,而是________物体运动状态的原因;揭示了一切物体都具有一种固有属性——________。
答案:
维持 改变 惯性
2. 如图所示,冰壶在冰面上的运动。如果摩擦阻力比较大,冰壶很快停下来;如果摩擦阻力很小,冰壶能滑得很远;如果摩擦阻力为0,冰壶将永远运动下去。

试结合上述现象分析:
(1) 牛顿第一定律中“除非作用在它上面的力迫使它改变这种状态”,说明运动与力有什么关系?
(2) 根据牛顿第一定律思考:如果物体不受外力作用,物体将处于什么状态?

试结合上述现象分析:
(1) 牛顿第一定律中“除非作用在它上面的力迫使它改变这种状态”,说明运动与力有什么关系?
(2) 根据牛顿第一定律思考:如果物体不受外力作用,物体将处于什么状态?
答案:
提示:
(1)说明力是改变物体运动状态的原因。
(2)不受外力时,原来静止的物体,仍然静止;原来运动的物体,速度保持不变,将永远做匀速直线运动。
(1)说明力是改变物体运动状态的原因。
(2)不受外力时,原来静止的物体,仍然静止;原来运动的物体,速度保持不变,将永远做匀速直线运动。
[微训练]
根据预习内容判断以下说法正误。
1. 牛顿第一定律是可以通过实验验证的。( )
2. 由牛顿第一定律可知,当一个做匀加速直线运动的物体所受外力全部消失时,物体将立刻静止。( )
3. 牛顿第一定律说明一切物体都具有惯性。( )
根据预习内容判断以下说法正误。
1. 牛顿第一定律是可以通过实验验证的。( )
2. 由牛顿第一定律可知,当一个做匀加速直线运动的物体所受外力全部消失时,物体将立刻静止。( )
3. 牛顿第一定律说明一切物体都具有惯性。( )
答案:
×
@@×
@@√
@@×
@@√
1. 惯性是指物体具有______________________的性质。
答案:
1.保持原来运动状态
2. 惯性是物体的________属性,________物体都具有惯性。
答案:
2.固有 一切
3. 惯性的唯一量度是________,惯性与物体的________以及________无关。
答案:
3.质量 运动状态 受力情况
[微训练]
根据预习内容判断以下说法正误。
1. 物体的惯性大小取决于物体的质量大小。( )
2. 物体只有处于静止状态或匀速直线运动状态时才有惯性。( )
根据预习内容判断以下说法正误。
1. 物体的惯性大小取决于物体的质量大小。( )
2. 物体只有处于静止状态或匀速直线运动状态时才有惯性。( )
答案:
1.√ 2.×
1. 关于伽利略理想实验,下列说法正确的是( )
A. 完全是理想的,没有以事实为基础,只有理想推理
B. 以可靠事实为基础,经科学抽象,深刻反映自然规律
C. 证实了亚里士多德关于力与运动的关系的观点
D. 证实了自由落体运动是匀变速直线运动
A. 完全是理想的,没有以事实为基础,只有理想推理
B. 以可靠事实为基础,经科学抽象,深刻反映自然规律
C. 证实了亚里士多德关于力与运动的关系的观点
D. 证实了自由落体运动是匀变速直线运动
答案:
B 解析:伽利略在研究力与运动的关系时,在斜面实验的基础上,成功地设计了理想斜面实验,他以实验事实为依据,抓住主要因素,忽略次要因素,从而能够更深刻地揭示自然规律。因此,理想实验是建立在实际事实基础上的合乎逻辑的科学推断,更深刻地反映了自然规律,故A错误,B正确;伽利略理想实验否定了亚里士多德关于力与运动的关系的观点,即否定了力是维持物体运动的原因的理论,故C错误;伽利略理想实验并没有证实自由落体运动是匀变速直线运动,故D错误。
2. 伽利略创造的把实验、假设和逻辑推理相结合的科学方法,有力地促进了人类科学认识的发展。利用如图所示的装置做如下实验:小球从左侧斜面上的〇点由静止释放后沿斜面向下运动,并沿右侧斜面上升。斜面上先后铺垫三种粗糙程度逐渐减小的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3。根据三次实验结果的对比,可以得到的最直接的结论是( )
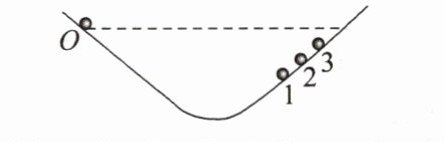
A. 如果斜面光滑,小球将上升到与〇点等高的位置
B. 如果小球不受力,它将一直保持匀速直线运动或静止状态
C. 如果小球受到力的作用,它的运动状态将发生改变
D. 小球受到的力一定时,质量越大,它的运动状态就越容易改变

A. 如果斜面光滑,小球将上升到与〇点等高的位置
B. 如果小球不受力,它将一直保持匀速直线运动或静止状态
C. 如果小球受到力的作用,它的运动状态将发生改变
D. 小球受到的力一定时,质量越大,它的运动状态就越容易改变
答案:
A 解析:根据题意,先后铺垫三种粗糙程度逐渐减小的材料时,小球上升高度一直增加,可推知,当斜面光滑,小球将上升到与初始点等高的位置,故A正确;本实验并不能得到力与运动状态的关系,故B、C错误;本实验小球质量是固定的,不能得到质量与运动状态之间的关系,故D错误。
3. 理想实验有时能更深刻地反映自然规律。伽利略设想了一个如图所示的理想实验,下列设想步骤中,有一个是可靠事实,其余的是推论。
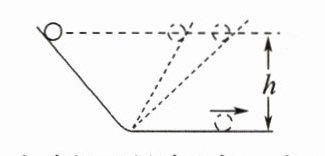
① 减小第二个斜面的倾角,小球在这个斜面上仍然要达到原来的高度;
② 两个对接的斜面,让静止的小球沿一个斜面滚下,小球将滚上另一个斜面;
③ 如果没有摩擦,小球将上升到原来释放时的高度;
④ 继续减小第二个斜面的倾角,最后使它变成水平面,小球将沿水平面持续做匀速直线运动。
(1) 请将上述理想实验的设想步骤按照正确的顺序排列:____________(填写序号即可)。
(2) 将上述设想步骤中的可靠事实和理想化推论进行分类。
属于可靠事实的步骤是________;
属于理想化推论的步骤是________。

① 减小第二个斜面的倾角,小球在这个斜面上仍然要达到原来的高度;
② 两个对接的斜面,让静止的小球沿一个斜面滚下,小球将滚上另一个斜面;
③ 如果没有摩擦,小球将上升到原来释放时的高度;
④ 继续减小第二个斜面的倾角,最后使它变成水平面,小球将沿水平面持续做匀速直线运动。
(1) 请将上述理想实验的设想步骤按照正确的顺序排列:____________(填写序号即可)。
(2) 将上述设想步骤中的可靠事实和理想化推论进行分类。
属于可靠事实的步骤是________;
属于理想化推论的步骤是________。
答案:
解析:伽利略理想实验是在可靠事实的基础上进行合理的推理,从而得到正确的结论。②是可靠事实,因此放在第一步,①③④是在无摩擦的情况下进行的理想化推论。
答案:
(1)②③①④
(2)② ①③④
答案:
(1)②③①④
(2)② ①③④
1. “自然和自然的法则在黑夜中隐藏;上帝说,让牛顿去吧!于是一切都被照亮”。自然在牛顿面前像是一本打开的书,许多自然的奥秘被牛顿用数学的方法一一破解。牛顿作为物理学的奠基人,为我们留下了诸多思想的宝藏。而其中可以称之为物理学的基石的方法既是后世物理人剖析世界的手术刀,也是同学们在每次解决物理问题过程中必须要做好的第一步,这种方法是指( )
A. 建构物理模型方法
B. 演绎推理法
C. 反证法
D. 控制变量法
A. 建构物理模型方法
B. 演绎推理法
C. 反证法
D. 控制变量法
答案:
A 解析:建构物理模型方法是每次解决物理问题过程中必须要做好的第一步。故选A。
2. (多选)下列对牛顿第一定律的理解正确的是( )
A. 牛顿第一定律反映了物体不受外力作用时的运动规律
B. 不受外力作用时,物体的运动状态保持不变
C. 在水平地面上滑动的木块最终停下来,是由于没有外力维持木块的运动
D. 飞跑的运动员,由于遇到障碍而被绊倒,这是因为他受到外力作用,迫使他改变原来的运动状态
A. 牛顿第一定律反映了物体不受外力作用时的运动规律
B. 不受外力作用时,物体的运动状态保持不变
C. 在水平地面上滑动的木块最终停下来,是由于没有外力维持木块的运动
D. 飞跑的运动员,由于遇到障碍而被绊倒,这是因为他受到外力作用,迫使他改变原来的运动状态
答案:
ABD 解析:牛顿第一定律反映了物体在不受外力作用时将保持匀速直线运动状态或静止状态,故A、B正确;水平地面上滑动的木块最终要停下来,是因为木块受到了摩擦力,故C错误;力是改变物体运动状态的原因,故物体运动状态发生改变时,一定受到了外力的作用,飞跑的运动员由于遇到障碍而被绊倒,这是因为他受到外力作用,迫使他改变原来的运动状态,故D正确。
3. 如图所示,一个劈形物体A(各面均光滑)放在固定的斜面上,上表面水平,在其上表面放一个光滑小球B。劈形物体A由静止开始释放,则小球B在碰到斜面前的运动轨迹是( )

A. 沿斜面向下的直线
B. 竖直向下的直线
C. 无规则的曲线
D. 抛物线

A. 沿斜面向下的直线
B. 竖直向下的直线
C. 无规则的曲线
D. 抛物线
答案:
B 解析:由于小球B处在劈形物体A上,接触面光滑,在劈形物体A下滑过程中,小球B在水平方向上不受外力作用,则小球B在水平方向上保持原来的静止状态,仅沿竖直方向运动,故B正确。
1. 如图所示的为月球车示意图,当该月球车分别在地面以较小的速率和在月面以较大的速率行驶时,下列判断正确的是( )

A. 在地面运动时的惯性较大
B. 在月面运动时的惯性较大
C. 在地面和月面惯性一样大
D. 在地面运动时的质量较大

A. 在地面运动时的惯性较大
B. 在月面运动时的惯性较大
C. 在地面和月面惯性一样大
D. 在地面运动时的质量较大
答案:
C 解析:惯性的大小仅与物体的质量有关,与物体的运动状态无关,所以当月球车分别在地面和月面行驶时惯性是一样大的,A、B错误,C正确;质量是物体的固有属性,是不变的,D错误。
2. (多选)在静止的列车上,有两个注满水的容器,容器中分别用细线系着铁球和乒乓球,在列车启动的过程中,小球所处状态表示正确的是(图中箭头表示列车启动方向)( )


答案:
BD 解析:列车由静止向右启动,铁球和水都有向右运动的趋势,但与同体积的“水球”相比,铁球质量大、惯性大,铁球的运动状态难以改变,即速度增加慢,而同体积的“水球”的运动状态容易改变,即速度增加快,而且水和容器一起运动,所以列车启动时,铁球相对于容器向左运动,故A错误,B正确;列车由静止向右启动,乒乓球和水都有向右运动的趋势,但与同体积的“水球”相比,乒乓球质量小、惯性小,乒乓球的运动状态容易改变,即速度增加快,而同体积的“水球”的运动状态相对更难以改变,即速度增加慢,而且水和容器一起运动,所以列车启动时,乒乓球相对于容器向右运动,故C错误,D正确。
3. 打水漂是古老的游戏之一(如图所示),仅需要一块小瓦片,在手上呈水平放置后,用力水平掷出,瓦片擦水面飞行,瓦片不断地在水面上向前弹跳,直至下沉,下列判断正确的是( )

A. 掷出时的初速度越大,瓦片的惯性一定越大
B. 飞行时所用时间越长,瓦片的惯性一定越大
C. 飞出去的距离越长,瓦片的惯性一定越大
D. 瓦片的质量越大,惯性一定越大

A. 掷出时的初速度越大,瓦片的惯性一定越大
B. 飞行时所用时间越长,瓦片的惯性一定越大
C. 飞出去的距离越长,瓦片的惯性一定越大
D. 瓦片的质量越大,惯性一定越大
答案:
D 解析:惯性是物体本身的固有属性,惯性的大小只与物体的质量有关,所以瓦片的质量越大,惯性一定越大,与初速度、时间、飞行距离等因素无关,故A、B、C错误,D正确。
实验目的
1. 学会用控制变量法研究物理规律。
2. 会测量加速度、力和质量,能作出物体运动的a−F、a−$\frac{1}{M}$图像。
3. 会通过实验探究加速度与力、质量的定量关系。
实验器材
小车、槽码、砝码、细绳、一端带有定滑轮的长木板、垫木、________、________、纸带、________天平。
#### 实验步骤
1. 安装实验器材:将小车置于带有定滑轮的木板上,将纸带穿过打点计时器后挂在小车尾部。
2. 补偿阻力:用薄垫块将木板一端垫高,调整其倾斜程度,直到小车在________(选填“受”或“不受”)牵引时能拖动纸带沿木板________运动。
3. 悬挂槽码:在细线一端挂上槽码,另一端通过定滑轮系在小车前端。

4. 收集纸带数据:将小车靠近打点计时器后开启打点计时器,并让小车由静止释放,打点计时器在纸带上打出一系列点,根据公式________计算出小车的加速度。
5. 改变小车受力
(1) 保持小车的质量不变,通过增加槽码的数量(总质量________小车质量)改变小车所受的拉力。接通电源后放开小车,用纸带记录小车的运动情况。取下纸带,并在纸带上标上编号及所挂槽码的总重力m₁g。
(2) 重复上述步骤(1),多做几次实验,并记录好相应纸带的编号及所挂槽码的总重力m₂g、m₃g……
6. 改变小车质量
(1) 保持小车所受的拉力不变,通过增加或减少小车上的砝码的方式,改变小车的质量。接通电源后放开小车,用纸带记录小车的运动情况。取下纸带,并在纸带上标上编号及小车和砝码的总质量M₁。
(2) 继续在小车上增减砝码,重复上述步骤(1),多做几次实验,在每次实验得到的纸带上标上编号及小车和砝码的总质量M₂、M₃……
1. 学会用控制变量法研究物理规律。
2. 会测量加速度、力和质量,能作出物体运动的a−F、a−$\frac{1}{M}$图像。
3. 会通过实验探究加速度与力、质量的定量关系。
实验器材
小车、槽码、砝码、细绳、一端带有定滑轮的长木板、垫木、________、________、纸带、________天平。
#### 实验步骤
1. 安装实验器材:将小车置于带有定滑轮的木板上,将纸带穿过打点计时器后挂在小车尾部。
2. 补偿阻力:用薄垫块将木板一端垫高,调整其倾斜程度,直到小车在________(选填“受”或“不受”)牵引时能拖动纸带沿木板________运动。
3. 悬挂槽码:在细线一端挂上槽码,另一端通过定滑轮系在小车前端。

4. 收集纸带数据:将小车靠近打点计时器后开启打点计时器,并让小车由静止释放,打点计时器在纸带上打出一系列点,根据公式________计算出小车的加速度。
5. 改变小车受力
(1) 保持小车的质量不变,通过增加槽码的数量(总质量________小车质量)改变小车所受的拉力。接通电源后放开小车,用纸带记录小车的运动情况。取下纸带,并在纸带上标上编号及所挂槽码的总重力m₁g。
(2) 重复上述步骤(1),多做几次实验,并记录好相应纸带的编号及所挂槽码的总重力m₂g、m₃g……
6. 改变小车质量
(1) 保持小车所受的拉力不变,通过增加或减少小车上的砝码的方式,改变小车的质量。接通电源后放开小车,用纸带记录小车的运动情况。取下纸带,并在纸带上标上编号及小车和砝码的总质量M₁。
(2) 继续在小车上增减砝码,重复上述步骤(1),多做几次实验,在每次实验得到的纸带上标上编号及小车和砝码的总质量M₂、M₃……
答案:
打点计时器 交流电源 刻度尺
@@不受 匀速
@@△x=aT²
@@远小于
@@不受 匀速
@@△x=aT²
@@远小于
1. 用如图所示的装置可以完成“探究加速度与力、质量的关系”实验。
(1) 打点计时器使用的电源是________(填选项前的字母)。

A. 直流电源 B. 交流电源
(2) 实验中需要补偿阻力,正确操作方法是______(填选项前的字母)。
A. 把长木板远离滑轮的一端垫高
B. 改变小车的质量
(3) 在________(填选项前的字母)且接通打点计时器电源的情况下,轻推一下小车,若小车拖着纸带匀速运动,表明已经补偿了阻力。
A. 不悬挂槽码
B. 悬挂槽码
(4) 实验中,为了保证悬挂槽码的重力近似等于使小车做匀加速运动的拉力,悬挂槽码的总质量m与小车质量M之间应满足的关系是________。
A. M>>m B. m>>M
(1) 打点计时器使用的电源是________(填选项前的字母)。

A. 直流电源 B. 交流电源
(2) 实验中需要补偿阻力,正确操作方法是______(填选项前的字母)。
A. 把长木板远离滑轮的一端垫高
B. 改变小车的质量
(3) 在________(填选项前的字母)且接通打点计时器电源的情况下,轻推一下小车,若小车拖着纸带匀速运动,表明已经补偿了阻力。
A. 不悬挂槽码
B. 悬挂槽码
(4) 实验中,为了保证悬挂槽码的重力近似等于使小车做匀加速运动的拉力,悬挂槽码的总质量m与小车质量M之间应满足的关系是________。
A. M>>m B. m>>M
答案:
(1)B
(2)A
(3)A
(4)A
(1)B
(2)A
(3)A
(4)A
2. 在“探究加速度与力、质量的关系”的实验中,计算出各纸带的加速度后,将测得的反映加速度a和力F关系的有关数据记录在表一中,将测得的反映加速度a和质量M 关系的有关数据记录在表二中。
表一

表二

(1) 请根据表中所列数据,分别在图甲、图乙中作出a−F图像和a−$\frac{1}{M}$图像。

(2) 由图像可以判定:当M一定时,a与F 成____________关系;当F一定时,a与M 成____________关系。
(3) 由a−F图像可知,M = ________kg。
(4) 由a−$\frac{1}{M}$图像可知,F = ________N(结果保留一位有效数字)。
表一

表二

(1) 请根据表中所列数据,分别在图甲、图乙中作出a−F图像和a−$\frac{1}{M}$图像。

(2) 由图像可以判定:当M一定时,a与F 成____________关系;当F一定时,a与M 成____________关系。
(3) 由a−F图像可知,M = ________kg。
(4) 由a−$\frac{1}{M}$图像可知,F = ________N(结果保留一位有效数字)。
答案:
(1)见解析图甲、乙
(2)正比 反比
(3)0.5
(4)4
(1)见解析图甲、乙
(2)正比 反比
(3)0.5
(4)4
3. 图甲为“探究加速度与力、质量的关系”的实验装置示意图,图中打点计时器打点的时间间隔用T表示,小车及车中的砝码的质量用M表示,盘及盘中砝码的质量用m表示,小车的加速度可由小车后面拖动的纸带上打出的点计算得出,完成以下小题:
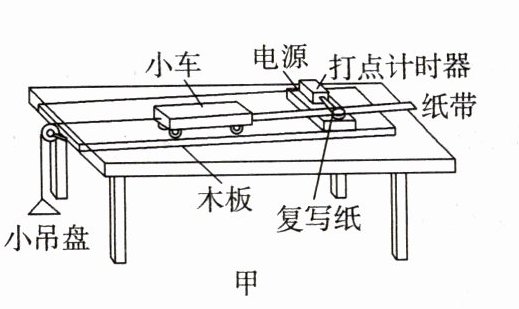
(1) 实验之前需要补偿阻力,补偿阻力的方法如下:将木板的右端垫高,让小车在木板上运动,直到小车在不受牵引时做________运动时为止。
(2) 如图乙所示,纸带上有O、A、B、C、D、E 和F等计数点,测得O到A的距离为s₁,A 到B的距离为s₂,用s₁、s₂和T表示出小车的加速度a = __________,A点的瞬时速度vₐ = ________。
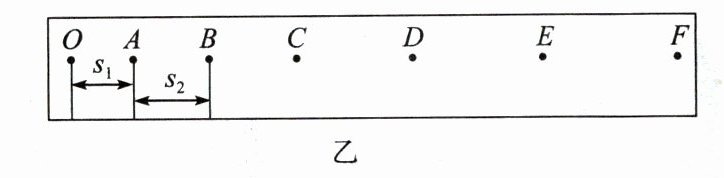
(3) 实验时,保持小吊盘及盘中砝码的质量一定,改变小车及车中砝码的质量,测出相应的加速度,采用图像法处理数据。为了较容易观测加速度α与质量M之间的关系,应该作出a与________的图像。
(4) 某小组同学,在做实验时忘记了补偿阻力,那么所得到的a−F图像关系可能是图中哪一个?(a是小车的加速度,F是细线作用于小车的拉力)________。


(1) 实验之前需要补偿阻力,补偿阻力的方法如下:将木板的右端垫高,让小车在木板上运动,直到小车在不受牵引时做________运动时为止。
(2) 如图乙所示,纸带上有O、A、B、C、D、E 和F等计数点,测得O到A的距离为s₁,A 到B的距离为s₂,用s₁、s₂和T表示出小车的加速度a = __________,A点的瞬时速度vₐ = ________。

(3) 实验时,保持小吊盘及盘中砝码的质量一定,改变小车及车中砝码的质量,测出相应的加速度,采用图像法处理数据。为了较容易观测加速度α与质量M之间的关系,应该作出a与________的图像。
(4) 某小组同学,在做实验时忘记了补偿阻力,那么所得到的a−F图像关系可能是图中哪一个?(a是小车的加速度,F是细线作用于小车的拉力)________。

答案:
(1)匀速
(2)$\frac{s_2 - s_1}{T^2}$ $\frac{s_2 + s_1}{2T}$
(3)$\frac{1}{M}$
(4)C
(1)匀速
(2)$\frac{s_2 - s_1}{T^2}$ $\frac{s_2 + s_1}{2T}$
(3)$\frac{1}{M}$
(4)C
4. 在“天宫课堂”中,我国航天员演示了利用牛顿第二定律测量物体质量的实验。受此启发,某同学利用气垫导轨、力传感器、加速度传感器、滑块、轻弹簧和待测物体等器材设计了测量物体质量的实验,如图甲所示。主要步骤如下:
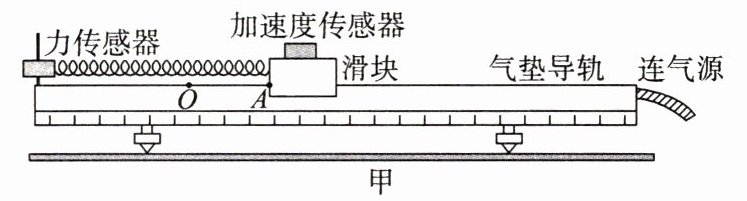
① 将力传感器固定在气垫导轨左端支架上,加速度传感器固定在滑块上。
② 接通气源,放上滑块,调平气垫导轨。
③ 将弹簧左端连接力传感器,右端连接滑块,弹簧处于原长时滑块左端位于〇点;A点到O点的距离为5.00cm,拉动滑块使其左端处于A点,由静止释放并开始计时。
④ 计算机采集获取数据,得到滑块所受弹力F、加速度a随时间t变化的图像,部分图像如图乙所示。

回答以下问题(结果均保留两位有效数字):
(1) 弹簧的劲度系数为________N/m。
(2) 该同学从图乙中提取某些时刻F与a 的数据,画出a−F图像如图丙中I所示,由此可得滑块与加速度传感器的总质量为________kg。
(3) 该同学在滑块上增加待测物体,重复上述实验步骤,在图丙中画出新的a−F图像II,则待测物体的质量为________kg。

① 将力传感器固定在气垫导轨左端支架上,加速度传感器固定在滑块上。
② 接通气源,放上滑块,调平气垫导轨。
③ 将弹簧左端连接力传感器,右端连接滑块,弹簧处于原长时滑块左端位于〇点;A点到O点的距离为5.00cm,拉动滑块使其左端处于A点,由静止释放并开始计时。
④ 计算机采集获取数据,得到滑块所受弹力F、加速度a随时间t变化的图像,部分图像如图乙所示。

回答以下问题(结果均保留两位有效数字):
(1) 弹簧的劲度系数为________N/m。
(2) 该同学从图乙中提取某些时刻F与a 的数据,画出a−F图像如图丙中I所示,由此可得滑块与加速度传感器的总质量为________kg。
(3) 该同学在滑块上增加待测物体,重复上述实验步骤,在图丙中画出新的a−F图像II,则待测物体的质量为________kg。
答案:
(1)12
(2)0.20
(3)0.13
(1)12
(2)0.20
(3)0.13
1. 表达式:根据上一节的实验可知,m 不变时 a - F 图像为过原点直线,则可以得出______,F 不变时,a - $\frac{1}{m}$ 图像为过原点直线,同样得出________,综合这个公式可得 a ∝ $\frac{F}{m}$,也可以写成等式________,这便是牛顿第二定律的表达式,注意公式中 F 是指________。
答案:
a=k₁F a=k₂$\frac{1}{m}$ F=kma 合力
2. “由 F = kma 可知,当 F = 0 时 a = 0,即物体静止或做匀速直线运动,所以牛顿第一定律是牛顿第二定律的特例。”这种说法正确吗,为什么?
答案:
提示:不正确。因为物体所受合力为0和不受任何外力作用是两种不同的状态。
微训练
1. 牛顿第二定律既明确了力、质量、加速度三者的数量关系,也明确了加速度与力的方向关系。( )
2. 由 F = kma 可知,物体所受的合外力与物体的质量成正比,与物体的加速度成反比。( )
3. 加速度的方向决定了合外力的方向。( )
1. 牛顿第二定律既明确了力、质量、加速度三者的数量关系,也明确了加速度与力的方向关系。( )
2. 由 F = kma 可知,物体所受的合外力与物体的质量成正比,与物体的加速度成反比。( )
3. 加速度的方向决定了合外力的方向。( )
答案:
√
@@×
@@×
@@×
@@×
1. “牛顿”的定义:使质量为 1kg 的物体产生__________的加速度的力叫作 1N,即 1N = ________。
答案:
1m/s² 1kg·m/s²
2. 将 F = kma 中的 k = 1,则表达式中 F、m、a 的单位分别为牛顿、________、米每二次方秒,牛顿第二定律可表达为____________。
答案:
千克 F=ma
[微训练]
1. 使质量为 1g 的物体产生 1cm/s²的加速度的力叫作 1N。( )
2. 公式 F = ma 中,各物理量的单位可以任意选取。( )
3. 牛顿第二定律表达式 F = kma 中的系数 k 总等于 1。( )
1. 使质量为 1g 的物体产生 1cm/s²的加速度的力叫作 1N。( )
2. 公式 F = ma 中,各物理量的单位可以任意选取。( )
3. 牛顿第二定律表达式 F = kma 中的系数 k 总等于 1。( )
答案:
×
@@×
@@×
@@×
@@×
1. 根据牛顿第二定律,下列叙述正确的是( )
A. 物体加速度的大小跟它的质量成反比,跟物体速度变化量成正比
B. 物体所受合力必须达到一定值时,才能使物体产生加速度
C. 当物体质量改变但其所受合力的水平分力不变时,物体水平加速度大小与质量成反比
D. 物体加速度的大小跟它所受作用力中的任一个力的大小都成正比
A. 物体加速度的大小跟它的质量成反比,跟物体速度变化量成正比
B. 物体所受合力必须达到一定值时,才能使物体产生加速度
C. 当物体质量改变但其所受合力的水平分力不变时,物体水平加速度大小与质量成反比
D. 物体加速度的大小跟它所受作用力中的任一个力的大小都成正比
答案:
C 解析:根据牛顿第二定律可知,物体加速度的大小跟其质量成反比,与速度及速度变化量无关,故A错误;力是产生加速度的原因,只要有力,就能产生加速度,力与加速度是瞬时对应的关系,故B错误;当物体质量改变但其所受合力的水平分力不变时,根据牛顿第二定律F=ma可知,物体水平方向的加速度大小与其质量成反比,故C正确;物体加速度的大小跟物体所受的合力成正比,而不是跟任一个力的大小成正比,故D错误。
2. (多选)关于速度、加速度、合力的关系,下列说法正确的是( )
A. 原来静止在光滑水平面上的物体,受到水平推力的瞬间,物体立刻获得加速度
B. 加速度的方向与合力的方向总是一致的,但与速度的方向可能相同,也可能不同
C. 在初速度为 0 的匀加速直线运动中,速度、加速度与合力的方向总是一致的
D. 合力变小,物体的速度一定变小
A. 原来静止在光滑水平面上的物体,受到水平推力的瞬间,物体立刻获得加速度
B. 加速度的方向与合力的方向总是一致的,但与速度的方向可能相同,也可能不同
C. 在初速度为 0 的匀加速直线运动中,速度、加速度与合力的方向总是一致的
D. 合力变小,物体的速度一定变小
答案:
ABC 解析:由牛顿第二定律可知选项A、B正确;初速度为0的匀加速直线运动中,速度、加速度与合力的方向相同,选项C正确;合力变小,加速度变小,但速度是变大还是变小取决于加速度与速度的方向关系,选项D错误。
3. 一个物理量,一般会有定义式、决定式及它与其他物理量的关系式三个式子,只有决定式才说明这个物理量是由哪些物理量决定及怎样决定的。关于决定加速度大小及方向的因素,下列说法错误的是( )
A. 速度变化量是加速度的决定因素之一
B. 合力的方向决定着加速度的方向
C. 合力大小是决定加速度大小的因素之一
D. 物体的质量也是加速度的决定因素
A. 速度变化量是加速度的决定因素之一
B. 合力的方向决定着加速度的方向
C. 合力大小是决定加速度大小的因素之一
D. 物体的质量也是加速度的决定因素
答案:
A 解析:由加速度的定义式a=$\frac{\Delta v}{t}$可知,速度变化量Δv不是加速度的决定因素之一,加速度只是在数值上等于单位时间内的速度变化量,故A错误,与题意相符;由加速度的决定式a=$\frac{F}{m}$可知,合力的方向决定着加速度的方向,合力大小是决定加速度大小的因素之一,物体的质量也是加速度的决定因素,故B、C、D正确,与题意不符。
山东号航空母舰在拖船的帮助下离港的过程如图所示,此过程中,航母会受到来自拖船的多个方向的力的作用。

(1) 知道每艘拖船对航母的力,如何求解航母的加速度?
(2) 知道航母的加速度和除一艘拖船外其余拖船的力,如何求解这一艘拖船的力?

(1) 知道每艘拖船对航母的力,如何求解航母的加速度?
(2) 知道航母的加速度和除一艘拖船外其余拖船的力,如何求解这一艘拖船的力?
答案:
提示:
(1)知道航母受到的每个力,先根据平行四边形定则求出航母受到的合力,再根据牛顿第二定律求航母的加速度。
(2)知道航母的加速度,先根据牛顿第二定律求出航母所受到的合力,再根据平行四边形定则求出这一艘拖船的力。
(1)知道航母受到的每个力,先根据平行四边形定则求出航母受到的合力,再根据牛顿第二定律求航母的加速度。
(2)知道航母的加速度,先根据牛顿第二定律求出航母所受到的合力,再根据平行四边形定则求出这一艘拖船的力。
1. 质量为 2.0×10⁵kg 的火箭,在地面发射时受到竖直向上、大小为 6.0×10⁶N 的推力,地面重力加速度取 g = 10m/s²,其加速度大小为( )
A. 4.0m/s²
B. 12m/s²
C. 20m/s²
D. 30m/s²
A. 4.0m/s²
B. 12m/s²
C. 20m/s²
D. 30m/s²
答案:
C 解析:根据牛顿第二定律可知F - mg = ma,解得a = $\frac{F - mg}{m}$ = $\frac{6×10 - 2×10×10}{2×10}$m/s² = 20m/s²,故选C。
2. 如图所示,位于水平地面上的质量为 M 的木块,在方向与水平面成α角、大小为 F 的拉力作用下,沿水平地面做匀加速直线运动(mg>Fsinα)。若木块与地面间的动摩擦因数为μ,则木块的加速度为( )

A. $\frac{F}{M}$
B. $\frac{Fcosα}{M}$
C. $\frac{F - μMg}{M}$
D. $\frac{Fcosα - μ(Mg - Fsinα)}{M}$

A. $\frac{F}{M}$
B. $\frac{Fcosα}{M}$
C. $\frac{F - μMg}{M}$
D. $\frac{Fcosα - μ(Mg - Fsinα)}{M}$
答案:
D 解析:木块受力如图所示,在竖直方向有Fₙ = Mg - Fsinα;在水平方向,由牛顿第二定律得Fcosα - μ(Mg - Fsinα) = Ma,解得加速度a = $\frac{Fcosα - μ(Mg - Fsinα)}{M}$,故选D。

D 解析:木块受力如图所示,在竖直方向有Fₙ = Mg - Fsinα;在水平方向,由牛顿第二定律得Fcosα - μ(Mg - Fsinα) = Ma,解得加速度a = $\frac{Fcosα - μ(Mg - Fsinα)}{M}$,故选D。

3. 将一个物体用弹簧测力计竖直悬挂起来后,弹簧测力计的示数如图甲所示(弹簧测力计的量程为 0 - 100N)。之后将该物体放到粗糙的水平面上,如图乙所示,当逐渐增大拉力到 43N 时,物体刚好运动。物体运动之后,只用 40N 的拉力就能使物体继续向右匀速运动。问:(取 g = 10m/s²)
(1) 物体的质量为多少?物体与地面间的最大静摩擦力为多大?
(2) 物体与地面间的动摩擦因数为多大?
(3) 如果将拉力改为 60N,并且从静止开始拉物体运动,经过 10s 时,物体的运动速度和位移各为多少?

(1) 物体的质量为多少?物体与地面间的最大静摩擦力为多大?
(2) 物体与地面间的动摩擦因数为多大?
(3) 如果将拉力改为 60N,并且从静止开始拉物体运动,经过 10s 时,物体的运动速度和位移各为多少?

答案:
解析:
(1)由题图甲可得G = 80N = mg,故物体的质量m = $\frac{G}{g}$ = 8.0kg。由题意知物体与地面间的最大静摩擦力Fₘₐₓ = 43N。
(2)物体在40N拉力作用下匀速运动时受力分析如图所示。
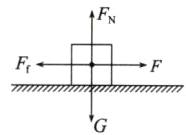
可得Fₙ = G = 80N,滑动摩擦力Ff = F = 40N,则μ = $\frac{F_f}{Fₙ}$ = $\frac{40N}{80N}$ = 0.5。
(3)拉力改为60N时,由牛顿第二定律知F合 = F' - Ff = ma,可得a = $\frac{F' - F_f}{m}$ = $\frac{60 - 40}{8.0}$m/s² = 2.5m/s²。速度v = at = 2.5×10m/s = 25m/s,位移x = $\frac{1}{2}$at² = $\frac{1}{2}$×2.5×10²m = 125m。
答案:
(1)8.0kg 43N
(2)0.5
(3)25m/s 125m
解析:
(1)由题图甲可得G = 80N = mg,故物体的质量m = $\frac{G}{g}$ = 8.0kg。由题意知物体与地面间的最大静摩擦力Fₘₐₓ = 43N。
(2)物体在40N拉力作用下匀速运动时受力分析如图所示。

可得Fₙ = G = 80N,滑动摩擦力Ff = F = 40N,则μ = $\frac{F_f}{Fₙ}$ = $\frac{40N}{80N}$ = 0.5。
(3)拉力改为60N时,由牛顿第二定律知F合 = F' - Ff = ma,可得a = $\frac{F' - F_f}{m}$ = $\frac{60 - 40}{8.0}$m/s² = 2.5m/s²。速度v = at = 2.5×10m/s = 25m/s,位移x = $\frac{1}{2}$at² = $\frac{1}{2}$×2.5×10²m = 125m。
答案:
(1)8.0kg 43N
(2)0.5
(3)25m/s 125m
4. 如图所示,将质量为 m = 0.2kg 的小球套在竖直固定的直杆上,小球的直径略大于杆的直径,小球与杆之间的动摩擦因数为μ = 0.5。现对小球施加一斜向上的拉力 F,使其以 2m/s²的加速度开始沿杆向上运动,拉力 F 与杆的夹角为θ = 53°,取 sin53° = 0.8,g = 10m/s²。求 F 的大小。
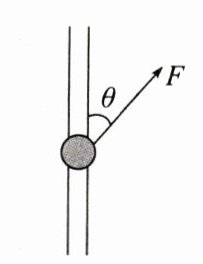

答案:
解析:根据牛顿第二定律可得Fcosθ - mg - Ff = ma。水平方向根据受力平衡可得Fsinθ = Fₙ。又Ff = μFₙ,联立解得F = 12N。
答案:12N
答案:12N
如图所示,用手向下压弹簧玩偶的头部,玩偶头部处于平衡状态。
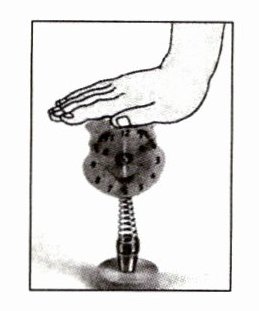
若人向下压的力为 F,弹簧玩偶的头部质量为 m,人手突然撤离时,会观察到什么现象?若是用手按在用轻杆支撑的刚性球上,人手突然撤离时,会观察到什么现象,试解释原因。

若人向下压的力为 F,弹簧玩偶的头部质量为 m,人手突然撤离时,会观察到什么现象?若是用手按在用轻杆支撑的刚性球上,人手突然撤离时,会观察到什么现象,试解释原因。
答案:
提示:人手按在玩偶上,突然撤离瞬间,弹簧长度没有发生变化,此瞬间弹力不变,玩偶所受弹力大于重力,玩偶有向上的加速度,因此会观察到玩偶向上弹起;人手按在用轻杆支撑的刚性球上时突然撤离瞬间,球所受弹力突变,此时弹力等于重力,球依然处于平衡状态。
1. 如图所示,一根弹簧一端固定在左侧竖直墙上,另一端连着小球 A,同时水平细线一端连着小球 A,另一端固定在右侧竖直墙上,弹簧与竖直方向的夹角是 60°,A、B 两小球分别连在另一根竖直弹簧两端。开始时 A、B 两小球都静止不动,A、B 两小球的质量相等,重力加速度大小为 g,若不计弹簧质量,在水平细线被剪断瞬间,A、B 两小球的加速度分别为( )
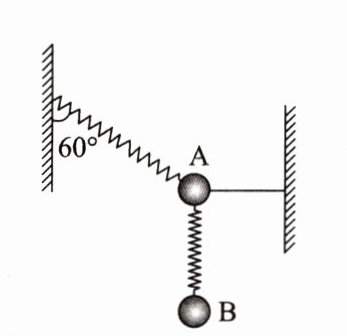
A. aA = aB = g
B. aA = 2g,aB = 0
C. aA = $\sqrt{3}$g,aB = 0
D. aA = $\sqrt{3}$g,aB = 0

A. aA = aB = g
B. aA = 2g,aB = 0
C. aA = $\sqrt{3}$g,aB = 0
D. aA = $\sqrt{3}$g,aB = 0
答案:
D 解析:水平细线被剪断前对A、B两小球进行受力分析,如图所示,由平衡条件得Fₜ = Fsin60°,Fcos60° = mₐg + F₁,F₁ = F₁' = mᵦg,又mₐ = mᵦ,解得Fₜ = 2$\sqrt{3}$mₐg;水平细线被剪断瞬间,Fₜ消失,弹簧弹力不能突变,A所受合力与Fₜ等大、反向,所以可得aₐ = $\frac{Fₜ}{mₐ}$ = 2$\sqrt{3}$g,aᵦ = 0,A、B、C错误,D正确。


D 解析:水平细线被剪断前对A、B两小球进行受力分析,如图所示,由平衡条件得Fₜ = Fsin60°,Fcos60° = mₐg + F₁,F₁ = F₁' = mᵦg,又mₐ = mᵦ,解得Fₜ = 2$\sqrt{3}$mₐg;水平细线被剪断瞬间,Fₜ消失,弹簧弹力不能突变,A所受合力与Fₜ等大、反向,所以可得aₐ = $\frac{Fₜ}{mₐ}$ = 2$\sqrt{3}$g,aᵦ = 0,A、B、C错误,D正确。


2. 如图所示,四只猴子水中捞月,它们将一颗又直又高的杨树压弯,竖直倒挂在树梢上,从上到下依次为 1、2、3、4 号猴子。正当 4 号猴子打算伸手捞“月亮”时,3 号猴子突然两手一滑没抓稳,4 号猴子扑通一声掉进了水里。假设 3 号猴子手滑前四只猴子都处于静止状态,四只猴子的质量都相等且为 m,重力加速度为 g,那么在 3 号猴子手滑后的一瞬间( )

A. 4 号猴子的加速度和速度都等于 0
B. 3 号猴子的加速度大小为 g,方向竖直向上
C. 2 号猴子对 3 号猴子的作用力大小为 $\frac{5mg}{3}$
D. 1 号猴子对 2 号猴子的作用力大小为 $\frac{8mg}{3}$

A. 4 号猴子的加速度和速度都等于 0
B. 3 号猴子的加速度大小为 g,方向竖直向上
C. 2 号猴子对 3 号猴子的作用力大小为 $\frac{5mg}{3}$
D. 1 号猴子对 2 号猴子的作用力大小为 $\frac{8mg}{3}$
答案:
D 解析:对4号猴子进行分析可得滑手后的一瞬间只受到重力,所以可得加速度大小为g,初速度为零,A错误;在手滑前,设树梢对猴子的作用力为Fₜ,对整体有Fₜ - 4mg = 0,当3号猴子手滑后的一瞬间,对1、2、3号猴子整体分析可得Fₜ - 3mg = 3ma',联立解得a' = $\frac{1}{3}$g,方向竖直向上,B错误;对3号猴子分析可得,2号猴子对3号猴子的作用力F,有F - mg = ma',可得F = $\frac{4}{3}$mg,C错误;对2、3号猴子进行受力分析可得F₁₂ - 2mg = 2ma',解得1号猴子对2号猴子的作用力大小为F₁₂ = $\frac{8mg}{3}$,D正确。
3. 如图所示,物块 1、2 间用刚性轻质杆相连,物块 3、4 间用轻质弹簧相连,物块 1、3 的质量均为 m,物块 2、4 的质量均为 M,两个系统均置于水平放置的光滑木板上,并处于静止状态。现将两木板沿水平方向突然抽出,设抽出后的瞬间,物块 1、2、3、4 的加速度大小分别为 a1、a2、a3、a4,重力加速度大小为 g,则有( )
A. a1 = a2 = a3 = a4 = 0
B. a1 = a2 = a3 = a4 = g
C. a1 = a2 = g,a3 = 0,a4 = $\frac{m + M}{M}$g
D. a1 = g,a2 = $\frac{m + M}{M}$g,a3 = 0,a4 = $\frac{m + M}{M}$g

A. a1 = a2 = a3 = a4 = 0
B. a1 = a2 = a3 = a4 = g
C. a1 = a2 = g,a3 = 0,a4 = $\frac{m + M}{M}$g
D. a1 = g,a2 = $\frac{m + M}{M}$g,a3 = 0,a4 = $\frac{m + M}{M}$g
答案:
C 解析:在抽出木板的瞬间,物块1、2与刚性轻杆接触处的形变立即消失,受到的合力均等于各自重力,由牛顿第二定律知a₁ = a₂ = g;而物块3、4间的轻弹簧的形变还来不及改变,此时弹簧对物块3向上的弹力大小和对物块4向下的弹力F大小仍为mg,因此物块3满足F = mg,则a₃ = 0;由牛顿第二定律得物块4满足F + Mg = Ma₄,则a₄ = $\frac{F + Mg}{M}$ = $\frac{M + m}{M}$g,所以C正确。
知识点一 基本单位
1. 根据物理量分为基本量和导出量,物理量的单位也分为________单位和________单位,物理学的________在确定了物理量之间的关系时,也确定了物理量的单位之间的关系。
1. 根据物理量分为基本量和导出量,物理量的单位也分为________单位和________单位,物理学的________在确定了物理量之间的关系时,也确定了物理量的单位之间的关系。
答案:
基本 导出 关系式
2. 如图所示,某运动员的最快速度可以达到10m/s,某人骑助力车的速度为35km/h。

(1)仅凭所给两个速度的数值能否判断运动员的速度与助力车的速度的大小关系?
(2)你能比较以上两个速度的大小关系吗?以上两个速度哪个大?

(1)仅凭所给两个速度的数值能否判断运动员的速度与助力车的速度的大小关系?
(2)你能比较以上两个速度的大小关系吗?以上两个速度哪个大?
答案:
提示:
(1)不能。
(2)能。10m/s = 36km/h>35km/h,所以运动员的最快速度较大。
(1)不能。
(2)能。10m/s = 36km/h>35km/h,所以运动员的最快速度较大。
[微训练]
根据预习内容判断以下说法正误。
1. 时间的单位s是基本单位。 ( )
2. 速度的单位m/s是导出单位。 ( )
3. 物理学的关系式表示了物理量间的数量关系和单位间的关系。 ( )
根据预习内容判断以下说法正误。
1. 时间的单位s是基本单位。 ( )
2. 速度的单位m/s是导出单位。 ( )
3. 物理学的关系式表示了物理量间的数量关系和单位间的关系。 ( )
答案:
√
@@√
@@√
@@√
@@√
知识点二 国际单位制
1. 1960年第11届国际计量大会制订了国际通用的国际单位制,规定了7个基本物理量的单位为基本单位。力学中有三个基本物理量,除了时间的单位是秒(s)以外,请你写出另外两个基本物理量的单位,它们分别是________和________。
1. 1960年第11届国际计量大会制订了国际通用的国际单位制,规定了7个基本物理量的单位为基本单位。力学中有三个基本物理量,除了时间的单位是秒(s)以外,请你写出另外两个基本物理量的单位,它们分别是________和________。
答案:
千克 米
2. 在下面列举的物理量单位中,属于国际单位制的是________,属于国际单位制的基本单位是________(填单位符号)。
A. ℃(摄氏度) B. K(开尔文)
C. atm(标准大气压) D. Pa(帕斯卡)
E. cmHg(厘米汞柱) F. m³(立方米)
G. L(升)
A. ℃(摄氏度) B. K(开尔文)
C. atm(标准大气压) D. Pa(帕斯卡)
E. cmHg(厘米汞柱) F. m³(立方米)
G. L(升)
答案:
BDF B
[微训练]
根据预习内容判断以下说法正误。
1. 质量、长度、时间是力学中的基本物理量。 ( )
2. 时间是国际单位制中的基本单位。 ( )
3. kg·m/s是国际单位制中的导出单位。 ( )
根据预习内容判断以下说法正误。
1. 质量、长度、时间是力学中的基本物理量。 ( )
2. 时间是国际单位制中的基本单位。 ( )
3. kg·m/s是国际单位制中的导出单位。 ( )
答案:
√
@@×
@@√
@@×
@@√
1. (2022·浙江6月选考)下列属于力的单位是 ( )
A. kg·m/s²
B. kg·m/s
C. kg·m²/s
D. kg·s/m²
A. kg·m/s²
B. kg·m/s
C. kg·m²/s
D. kg·s/m²
答案:
A 解析:根据牛顿第二定律有F = ma,则力的单位为kg·m/s²,故选A。
2. 测量“国际单位制选定的三个力学基本物理量”所用的仪器是 ( )
A. 刻度尺、弹簧测力计、停表
B. 刻度尺、弹簧测力计、打点计时器
C. 量筒、天平、停表
D. 刻度尺、天平、停表
A. 刻度尺、弹簧测力计、停表
B. 刻度尺、弹簧测力计、打点计时器
C. 量筒、天平、停表
D. 刻度尺、天平、停表
答案:
D 解析:国际单位制选定的三个力学基本物理量是长度、质量、时间,对应的测量仪器是刻度尺、天平、停表。故选D。
3. 国际单位制(SI)定义了7个基本单位,其他单位均可根据物理关系导出。1967年用铯−133原子基态的两个超精细能级间跃迁辐射的频率△ν = 9192631770Hz定义秒(s);1983年用真空中的光速c = 299792458m/s定义米(m)。2018年第26届国际计量大会决定,7个基本单位全部用基本物理常量来定义。关于国际单位制,下列选项不正确的是 ( )
A. 7个基本单位全部用物理常量定义,保证了基本单位的稳定性
B. 在力学范围内的基本单位有米(m)、千克(kg)、秒(s)
C. 牛顿是导出单位,1N = 1kg·m/s²
D. 米每二次方秒(m/s²)、牛顿每千克(N/kg)都是重力加速度g的单位
A. 7个基本单位全部用物理常量定义,保证了基本单位的稳定性
B. 在力学范围内的基本单位有米(m)、千克(kg)、秒(s)
C. 牛顿是导出单位,1N = 1kg·m/s²
D. 米每二次方秒(m/s²)、牛顿每千克(N/kg)都是重力加速度g的单位
答案:
C 解析:国际单位制中的7个基本单位全部用物理常量定义,保证了基本单位的稳定性,A正确;在力学范围内的基本单位有米(m)、千克(kg)、秒(s),B正确;牛顿是导出单位,1N = 1kg·m/s²,C错误;根据a = $\frac{F}{m}$可知,米每二次方秒(m/s²)、牛顿每千克(N/kg)都是重力加速度g的单位,D正确。本题选择不正确的,故选C。
4. 现有以下一些物理量和单位,按下面的要求选择填空。
A. 密度 B. 米/秒 C. 牛顿 D. 加速度
E. 质量 F. 秒 G. 厘米 H. 长度
I. 时间 J. 千克
(1)属于物理量的是____________。
(2)在国际单位制中,被选定的基本量是________。
(3)在国际单位制中,属于基本单位的是________,属于导出单位的是________。
A. 密度 B. 米/秒 C. 牛顿 D. 加速度
E. 质量 F. 秒 G. 厘米 H. 长度
I. 时间 J. 千克
(1)属于物理量的是____________。
(2)在国际单位制中,被选定的基本量是________。
(3)在国际单位制中,属于基本单位的是________,属于导出单位的是________。
答案:
解析:
(1)此题中给定的选项内,属于物理量的有密度、加速度、质量、长度、时间,故此空填ADEHI。
(2)此题中给定的选项内,在国际单位制中,被选定的基本量有质量、长度、时间,故此空填EHI。
(3)此题中给定的选项内,在国际单位制中,属于基本单位的有千克、秒,属于导出单位的有米/秒、牛顿,故第一个空填FJ,第二个空填BC。
答案:
(1)ADEHI
(2)EHI
(3)FJ BC
(1)此题中给定的选项内,属于物理量的有密度、加速度、质量、长度、时间,故此空填ADEHI。
(2)此题中给定的选项内,在国际单位制中,被选定的基本量有质量、长度、时间,故此空填EHI。
(3)此题中给定的选项内,在国际单位制中,属于基本单位的有千克、秒,属于导出单位的有米/秒、牛顿,故第一个空填FJ,第二个空填BC。
答案:
(1)ADEHI
(2)EHI
(3)FJ BC
任务二 单位制的应用
1. 一物体在2N的外力作用下,产生10cm/s²的加速度,要求求出该物体的质量。下面有几种不同的求法,其中单位运用正确、简洁而又规范的是 ( )
A. m = $\frac{F}{a}$ = $\frac{2}{10}$kg = 0.2kg
B. m = $\frac{F}{a}$ = $\frac{2N}{0.1m/s²}$ = 20$\frac{kg·m/s²}{m/s²}$ = 20kg
C. m = $\frac{F}{a}$ = $\frac{2}{0.1}$kg = 20kg
D. m = $\frac{F}{a}$ = $\frac{2}{0.1}$ = 20kg
1. 一物体在2N的外力作用下,产生10cm/s²的加速度,要求求出该物体的质量。下面有几种不同的求法,其中单位运用正确、简洁而又规范的是 ( )
A. m = $\frac{F}{a}$ = $\frac{2}{10}$kg = 0.2kg
B. m = $\frac{F}{a}$ = $\frac{2N}{0.1m/s²}$ = 20$\frac{kg·m/s²}{m/s²}$ = 20kg
C. m = $\frac{F}{a}$ = $\frac{2}{0.1}$kg = 20kg
D. m = $\frac{F}{a}$ = $\frac{2}{0.1}$ = 20kg
答案:
C 解析:物理计算中,在进行数量运算的同时,也要注意单位运算。带单位运算时,每一个数据均要带上单位,且单位换算要准确;也可以把题中已知量的单位都用国际单位制单位表示,计算的结果一定是国际单位制单位,这样在统一已知量的单位后,就不必一一写出各个量的单位,只在结果后面写出正确单位即可。在备选的四个选项中,A、D均错误,B项解题过程正确,但不简洁,只有C项中单位运用正确,且过程简洁、规范。
2. 研究发现,声音在气体中的传播速度仅取决于气体的压强、密度及某些常数(没有单位)。某人根据单位制的知识推导出了计算气体中声速的公式,并计算出声音在压强为1.00×10⁵Pa、密度为1.29kg/m³和压强为1.29×10⁵Pa、密度为1.44kg/m³的两种气体中的声速之比,正确的结果是 ( )
A. 25:36
B. 40:43
C. 43:40
D. 36:25
A. 25:36
B. 40:43
C. 43:40
D. 36:25
答案:
B 解析:由单位制知识建立声速表达式。等号左边:声速v,国际单位制单位是m/s;等号右边:密度ρ,国际单位制单位是kg/m³,压强p,国际单位制单位是Pa,又1Pa = 1N/m²,1N = 1kg·m/s²,整理后p的单位为kg/(m·s²)。等号两边的单位要统一,即p与ρ经过某种运算后所得的单位应该与声速v的单位m/s一致。我们观察p与ρ的单位,很容易看出$\sqrt{\frac{p}{ρ}}$的单位就是m/s,所以计算气体中声速的公式为v = k$\sqrt{\frac{p}{ρ}}$,其中k为常数,没有单位。将题中数据代入公式,则k = $\frac{v}{\sqrt{\frac{p}{ρ}}}$ = $\frac{40}{\sqrt{\frac{43}{1}}}$。故选B。
3. “血沉”是指红细胞在一定条件下沉降的速度,在医学中具有重要意义。测量“血沉”可将经过处理后的血液放进血沉管内,由于重力作用,血液中的红细胞将会下沉。设血沉管竖直放置且足够深,红细胞的形状为球体。已知红细胞下落受到血液的黏滞阻力表达式为f = 6πηrv,其中η为血液的黏滞系数,r为红细胞半径,v为红细胞运动的速率。若某血样中半径为r的红细胞,由静止下沉直到匀速运动的速度为vm,红细胞密度为ρ₁,血液的密度为ρ₂。以下说法正确的是 ( )
A. 该红细胞先做匀加速运动,后做匀速运动
B. 该红细胞的半径可表示为r = $\sqrt{\frac{9ηv_m}{2g(ρ_1 - ρ_2)}}$
C. 若血样中红细胞的半径较小,则红细胞匀速运动的速度较大
D. 若采用国际单位制中的基本单位来表示η的单位,则其单位为$\frac{kg}{m·s}$
A. 该红细胞先做匀加速运动,后做匀速运动
B. 该红细胞的半径可表示为r = $\sqrt{\frac{9ηv_m}{2g(ρ_1 - ρ_2)}}$
C. 若血样中红细胞的半径较小,则红细胞匀速运动的速度较大
D. 若采用国际单位制中的基本单位来表示η的单位,则其单位为$\frac{kg}{m·s}$
答案:
B 解析:红细胞在下沉过程中,根据牛顿第二定律,有mg - f - F浮 = ma,向下运动过程中,速度增大,阻力增大,加速度减小,当加速度减小到0时,速度达到最大,所以红细胞先做加速度减小的加速运动,后做匀速直线运动,故A错误;当红细胞匀速时mg = f + F浮,红细胞的质量为m = ρ₁·$\frac{4}{3}$πr³,浮力为F浮 = ρ₂·$\frac{4}{3}$πr³g,联立可得ρ₁·$\frac{4}{3}$πr³g = 6πηr vₘ + ρ₂·$\frac{4}{3}$πr³g,解得r = $\sqrt{\frac{9ηvₘ}{2g(ρ₁ - ρ₂)}}$,故B正确;由上述分析可知,若血样中红细胞的半径较小,则红细胞匀速运动的速度较小,故C错误;由黏滞阻力公式f = 6πηr v可知η = $\frac{f}{6πr v}$,故采用国际单位制中的基本单位来表示η的单位为$\frac{kg}{m·s}$,故D错误。
1. 从受力确定运动情况:已知物体的受力情况,根据牛顿第二定律求出物体的________,再根据物体的运动学条件(初、末位置和初、末速度及运动时间等),通过________确定物体的运动情况。
答案:
加速度 运动学规律
2. 中国有则《守株待兔》的成语故事,如图所示,设兔子的头部受到大小等于自身重力的打击力时,即可致死。假设兔子与树桩撞击后的速度为0,作用时间大约为0.2s,取g = 10m/s²,若要兔子被撞死,则它奔跑的速度至少为________m/s。

答案:
提示:兔子的头部受到大小等于自身重力的打击力时,即可致死,则兔子撞击树桩时的加速度大小为a = g = 10m/s²,则兔子奔跑的速度至少为v = at = 2m/s。
根据预习内容判断以下说法正误。
1. 物体的加速度方向就是其运动方向。( )
2. 同一个物体,其所受合外力越大,加速度越大。( )
3. 同一个物体,其所受合外力越大,运动越快。( )
1. 物体的加速度方向就是其运动方向。( )
2. 同一个物体,其所受合外力越大,加速度越大。( )
3. 同一个物体,其所受合外力越大,运动越快。( )
答案:
×
@@√
@@×
@@√
@@×
1. 从运动情况确定受力:已知物体的运动情况,根据运动学规律求出物体的________,再根据牛顿第二定律求出物体所受的____,进而知道物体的受力情况。
答案:
加速度 合外力
2. 动力学两类基本问题的思维程序图如下:
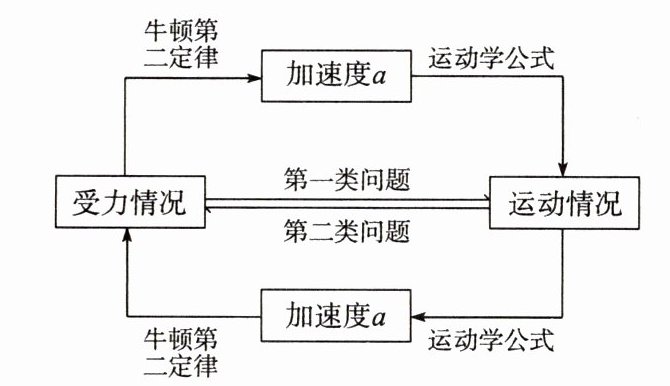
由图可见,不论求解哪一类问题,求解的关键是什么?

由图可见,不论求解哪一类问题,求解的关键是什么?
答案:
提示:解答动力学问题的关键是求加速度,求加速度有两种方法,一是利用运动学规律求解,二是利用牛顿第二定律求解。
根据预习内容判断以下说法正误。
1. 在水平粗糙地面上匀速运动的物体,外力撤去后将立即停止运动。( )
2. 由运动学公式求加速度,并由加速度的方向确定合外力的方向。( )
1. 在水平粗糙地面上匀速运动的物体,外力撤去后将立即停止运动。( )
2. 由运动学公式求加速度,并由加速度的方向确定合外力的方向。( )
答案:
1.× 2.√
2022年11月29日23时08分,搭载神舟十五号载人飞船的长征二号F遥十五运载火箭在酒泉卫星发射中心点火发射成功。

现场指挥倒计时结束发出点火命令后,立刻计时,测得火箭底部通过发射架的时间是t,如果要求出火箭受到的推力,还要知道哪些条件?不计空气阻力,假设火箭质量不变。

现场指挥倒计时结束发出点火命令后,立刻计时,测得火箭底部通过发射架的时间是t,如果要求出火箭受到的推力,还要知道哪些条件?不计空气阻力,假设火箭质量不变。
答案:
提示:根据牛顿第二定律F - mg = ma可知,若要求得推力F,还要知道火箭的质量和加速度,火箭的加速度可以根据运动学公式x = $\frac{1}{2}$at²求得,即需要知道发射架的高度x和火箭通过发射架的时间t。综上所述除了时间t已经测得外,还要知道火箭质量m和发射架的高度x。
1. 如图所示,向前行驶的车厢内有一面向行驶方向的乘客,乘客与车厢保持相对静止,座椅旁边有一小球用细线悬挂在车厢的天花板上,悬线与竖直方向成θ角且也与车厢相对静止,下列说法正确的是( )

A. 乘客受到的合力方向与运动方向相同
B. 车厢的速度越大,悬线与竖直方向的夹角θ越大
C. 车厢对乘客的作用力F一定大于乘客的重力G
D. 悬线与竖直方向的夹角θ增大,车厢对乘客作用力F可能不变

A. 乘客受到的合力方向与运动方向相同
B. 车厢的速度越大,悬线与竖直方向的夹角θ越大
C. 车厢对乘客的作用力F一定大于乘客的重力G
D. 悬线与竖直方向的夹角θ增大,车厢对乘客作用力F可能不变
答案:
1.C解析:由题图可知,小球受合外力方向与车厢运动方向相反,可知车厢做匀减速运动,乘客受到的合力方向也与运动方向相反,选项A错误;对小球,根据牛顿第二定律可知mgtanθ = ma,可得a = gtanθ,则车厢的加速度越大,悬线与竖直方向的夹角θ越大,但是速度大,θ不一定大,选项B错误;对乘客受力分析可知,车厢对乘客的作用力大小为F = $\sqrt{(mg)²+(ma)²}$>mg,即F一定大于乘客的重力G,选项C正确;悬线与竖直方向的夹角θ增大,则加速度a变大,车厢对乘客作用力F增大,选项D错误。
2. (2023·全国甲卷)(多选)用水平拉力使质量分别为m甲、m乙的甲、乙两物体在水平桌面上由静止开始沿直线运动,两物体与桌面间的动摩擦因数分别为μ甲和μ乙。甲、乙两物体运动后,所受拉力F与其加速度a的关系图线如图所示。由图可知( )

A. m甲<m乙
B. m甲>m乙
C. μ甲<μ乙
D. μ甲>μ乙

A. m甲<m乙
B. m甲>m乙
C. μ甲<μ乙
D. μ甲>μ乙
答案:
2.BC解析:根据牛顿第二定律有F - μmg = ma,整理后得F = ma + μmg,则可知F - a图像的斜率为m,纵截距为μmg,则由题图可看出m甲>m乙,μ甲m甲g = μ乙m乙g,则μ甲<μ乙,故选B、C。
3. (2022·浙江6月选考)通过滑轨把货物直接装运到卡车中。如图所示,倾斜滑轨与水平面成24°角,长度l₁ = 4m,水平滑轨长度可调,两滑轨间平滑连接。若货物从倾斜滑轨顶端由静止开始下滑,其与滑轨间的动摩擦因数均为μ = $\frac{2}{9}$,货物可视为质点(取g = 10m/s²,sin24° = 0.4,cos24° = 0.9)。
(1)求货物在倾斜滑轨上滑行时加速度a₁的大小。
(2)求货物在倾斜滑轨末端时速度v的大小。
(3)若货物滑离水平滑轨末端时的速度不超过2m/s,求水平滑轨的最短长度l₂。

(1)求货物在倾斜滑轨上滑行时加速度a₁的大小。
(2)求货物在倾斜滑轨末端时速度v的大小。
(3)若货物滑离水平滑轨末端时的速度不超过2m/s,求水平滑轨的最短长度l₂。

答案:
3.解析:
(1)货物在倾斜滑轨上滑行时,根据牛顿第二定律可得mgsin24° - μmgcos24° = ma₁,代入数据解得a₁ = 2m/s²。
(2)货物在倾斜滑轨上做匀加速直线运动,根据运动学公式有2a₁l₁ = v₁²,解得v₁ = 4m/s。
(3)货物在水平滑轨上做匀减速直线运动,根据牛顿第二定律有μmg = ma₂,根据运动学公式有 - 2a₂l₂ = v₂² - v₁²,代入数据联立解得l₂ = 2.7m。
答案:
(1)2m/s²
(2)4m/s
(3)2.7m
(1)货物在倾斜滑轨上滑行时,根据牛顿第二定律可得mgsin24° - μmgcos24° = ma₁,代入数据解得a₁ = 2m/s²。
(2)货物在倾斜滑轨上做匀加速直线运动,根据运动学公式有2a₁l₁ = v₁²,解得v₁ = 4m/s。
(3)货物在水平滑轨上做匀减速直线运动,根据牛顿第二定律有μmg = ma₂,根据运动学公式有 - 2a₂l₂ = v₂² - v₁²,代入数据联立解得l₂ = 2.7m。
答案:
(1)2m/s²
(2)4m/s
(3)2.7m
4. 滑冰车是儿童喜欢的冰上娱乐项目之一,如图所示,小明妈妈正与小明在冰上游戏。小明与冰车的总质量是40kg,冰车与冰面之间的动摩擦因数为0.05。在某次游戏中,假设小明妈妈对冰车施加了40N的水平推力,在冰车从静止开始运动10s后,停止施加力的作用,使冰车自由滑行(假设运动过程中冰车始终沿直线运动,小明始终没有施加力的作用,取g = 10m/s²)。求:
(1)冰车的最大速率;
(2)冰车在整个运动过程中滑行的总位移的大小。

(1)冰车的最大速率;
(2)冰车在整个运动过程中滑行的总位移的大小。

答案:
4.解析:
(1)以小明与冰车为研究对象,由牛顿第二定律得F - μmg = ma₁,v₁ = a₁t。
联立解得a₁ = 0.5m/s²,v₁ = 5m/s。
(2)冰车匀加速运动过程中有x₁ = $\frac{1}{2}$a₁t²,冰车自由滑行时有μmg = ma₂,v₁² = 2a₂x₂。
又x = x₁ + x₂。
联立解得x = 50m。
答案:
(1)5m/s
(2)50m
(1)以小明与冰车为研究对象,由牛顿第二定律得F - μmg = ma₁,v₁ = a₁t。
联立解得a₁ = 0.5m/s²,v₁ = 5m/s。
(2)冰车匀加速运动过程中有x₁ = $\frac{1}{2}$a₁t²,冰车自由滑行时有μmg = ma₂,v₁² = 2a₂x₂。
又x = x₁ + x₂。
联立解得x = 50m。
答案:
(1)5m/s
(2)50m
一运动员滑雪时的照片如图所示。

如果知道运动员在下滑过程中的运动时间、位移等,如何确定其受力情况?

如果知道运动员在下滑过程中的运动时间、位移等,如何确定其受力情况?
答案:
提示:先根据运动学公式,比如v = v₀ + at,x = v₀t + $\frac{1}{2}$at²,v² - v₀² = 2ax等,求得运动员的加速度,再由牛顿第二定律确定运动员的受力情况。
1. 如图甲所示,小物块从足够长的光滑斜面顶端由静止自由滑下。下滑位移为x时的速度为v,其x - v²图像如图乙所示,取g = 10m/s²,则斜面倾角θ为( )

A. 30°
B. 45°
C. 60°
D. 75°

A. 30°
B. 45°
C. 60°
D. 75°
答案:
1.A解析:小物块初速度为0,根据运动学公式有x = $\frac{v²}{2a}$,结合题图乙有$\frac{1}{2a}$ = $\frac{1}{10}$s²/m,则a = 5m/s²,对小物块受力分析,根据牛顿第二定律有F = mgsinθ = ma,可得sinθ = 0.5,则θ = 30°,A正确。
2. 放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系如图甲所示;物块的运动速度v与时间t的关系如图乙所示,6s后的速度图像没有画出,取g = 10m/s²。下列说法正确的是( )

A. 滑动时物块所受的摩擦力大小是3N
B. 物块的质量为1.5kg
C. 物块在6 - 9s内的加速度大小是1.5m/s²
D. 物块前6s内的平均速度大小是4.0m/s

A. 滑动时物块所受的摩擦力大小是3N
B. 物块的质量为1.5kg
C. 物块在6 - 9s内的加速度大小是1.5m/s²
D. 物块前6s内的平均速度大小是4.0m/s
答案:
2.B解析:由速度 - 时间图像可知,在3 - 6s内,物块处于匀速直线运动状态,即物块所受的摩擦力大小与推力F大小相等,则Ff = F₂ = 6N,故A错误;在0 - 3s内,物块做匀加速直线运动,a₁ = 2m/s²,F合 = ma₁ = F₁ - Ff = 3N,得出m = 1.5kg,故B正确;在6 - 9s内,F合 = ma₃ = Ff - F₃ = 3N,得出a₃ = 2m/s²,故C错误;由速度 - 时间图像与时间轴围的“面积”可知,0 - 6s内物体的位移x = $\frac{1}{2}$×(3 + 6)×6m = 27m,物块前6s内的平均速度大小v = $\frac{x}{t}$ = 4.5m/s,故D错误。
3. 如图所示,一质量为m = 0.6kg的小物块,在与斜面成α = 37°角的拉力F作用下,以$v_0 = 3m/s$的初速度沿斜面向上做匀加速运动,经t = 2s的时间物块由A点运动到B点,A、B之间的距离l = 10m。已知斜面倾角θ = 30°,物块与斜面之间的动摩擦因数μ = 0.5。取g = 10m/s²,sin37° = 0.6,cos37° = 0.8,求:
(1)物块加速度的大小及到达B点时速度的大小;
(2)拉力F的大小。

(1)物块加速度的大小及到达B点时速度的大小;
(2)拉力F的大小。

答案:
3.解析:
(1)设物块加速度的大小为a,到达B点时速度的大小为v,由运动学公式得l = v₀t + $\frac{1}{2}$at²,v = v₀ + at。
代入数据,联立解得a = 2m/s²,v = 7m/s。
(2)设物块所受支持力为FN,所受摩擦力为Ff,受力分析如图所示。

由牛顿第二定律得Fcosα - mgsinθ - Ff = ma,Fsinα + FN - mgcosθ = 0。
又Ff = μFN。
联立解得F = 6.18N。
答案:
(1)2m/s² 7m/s
(2)6.18N
3.解析:
(1)设物块加速度的大小为a,到达B点时速度的大小为v,由运动学公式得l = v₀t + $\frac{1}{2}$at²,v = v₀ + at。
代入数据,联立解得a = 2m/s²,v = 7m/s。
(2)设物块所受支持力为FN,所受摩擦力为Ff,受力分析如图所示。

由牛顿第二定律得Fcosα - mgsinθ - Ff = ma,Fsinα + FN - mgcosθ = 0。
又Ff = μFN。
联立解得F = 6.18N。
答案:
(1)2m/s² 7m/s
(2)6.18N
4. 在游乐场,有一种大型游乐设施跳楼机,如图所示,参加游戏的游客被安全带固定在座椅上,提升到离地最大高度64m处,然后由静止释放,开始下落阶段可认为是做自由落体运动,然后受到一恒定阻力而做匀减速运动,且下落到离地面4m高处时速度恰好减为0。已知游客和座椅总质量为1500kg,下落过程中最大速度为20m/s,取g = 10m/s²,求:
(1)游客下落过程的总时间;
(2)恒定阻力的大小。

(1)游客下落过程的总时间;
(2)恒定阻力的大小。

答案:
4.解析:
(1)下落过程的最大速度为vm = 20m/s,由v² = 2gh₁,vm = gt₁可得,游客下落过程中自由落体过程对应的时间t₁ = 2s,自由落体过程中下落高度h₁ = 20m。
设游客匀减速下落过程中下落高度为h₂,加速度大小为a₂,则vm² = 2a₂h₂,h₂ = 64m - 4m - h₁ = 40m,可得a₂ = 5m/s²。
由vm - a₂t₂ = 0可得游客匀减速下落的时间为t₂ = 4s。
游客下落过程的总时间t = t₁ + t₂ = 6s。
(2)设匀减速过程中所受恒定阻力大小为Ff,由牛顿第二定律可得Ff - mg = ma₂,解得Ff = m(a₂ + g) = 2.25×10⁴N。
答案:
(1)6s
(2)2.25×10⁴N
(1)下落过程的最大速度为vm = 20m/s,由v² = 2gh₁,vm = gt₁可得,游客下落过程中自由落体过程对应的时间t₁ = 2s,自由落体过程中下落高度h₁ = 20m。
设游客匀减速下落过程中下落高度为h₂,加速度大小为a₂,则vm² = 2a₂h₂,h₂ = 64m - 4m - h₁ = 40m,可得a₂ = 5m/s²。
由vm - a₂t₂ = 0可得游客匀减速下落的时间为t₂ = 4s。
游客下落过程的总时间t = t₁ + t₂ = 6s。
(2)设匀减速过程中所受恒定阻力大小为Ff,由牛顿第二定律可得Ff - mg = ma₂,解得Ff = m(a₂ + g) = 2.25×10⁴N。
答案:
(1)6s
(2)2.25×10⁴N
1. 如图所示,轻质滑轮两侧轻绳子上分别系有小球A和小球B,两球质量分别为$m_A$、$m_B$,两球从静止开始运动后,小球A下降,小球B上升。重力加速度为g,两球运动过程中轻绳拉力为( )
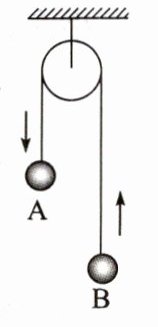
A. $\frac{m_Am_B}{m_A + m_B}g$
B. $\frac{2m_Am_B}{m_A + m_B}g$
C. $m_Ag$
D. $m_Bg$

A. $\frac{m_Am_B}{m_A + m_B}g$
B. $\frac{2m_Am_B}{m_A + m_B}g$
C. $m_Ag$
D. $m_Bg$
答案:
1.B解析:对A、B整体由牛顿第二定律可得mAg - mBg = (mA + mB)a,解得a = $\frac{mAg - mBg}{mA + mB}$,对A由牛顿第二定律可得mAg - FT = mAa,解得FT = $\frac{2mAmB}{mA + mB}$g,故B正确,A、C、D错误。
2. (多选)在一东西向的水平直铁轨上,停放着一列已用挂钩连接好的车厢。当机车在东边拉着这列车厢以大小为a的加速度向东行驶时,连接某两相邻车厢的挂钩P和Q间的拉力大小为F;当机车在西边拉着车厢以大小为$\frac{2}{3}a$的加速度向西行驶时,P和Q间的拉力大小仍为F。不计车厢与铁轨间的摩擦,每节车厢质量相同,则这列车厢的节数可能为( )
A. 8
B. 10
C. 15
D. 18
A. 8
B. 10
C. 15
D. 18
答案:
2.BC解析:设这列车厢的节数为n,P、Q挂钩西边有k节车厢,每节车厢的质量为m,由牛顿第二定律可知$\frac{F}{km}$ = $\frac{2}{3}$·$\frac{F}{(n - k)m}$,解得k = $\frac{3}{5}$n,k是正整数,则n只能取5的倍数,故B、C正确,A、D错误。
3. 如图所示,质量为M的斜面体A置于粗糙水平地面上,斜面体与水平地面间的动摩擦因数为μ,物体B与斜面间无摩擦。在水平向左的推力F作用下,A与B一起做匀加速直线运动,两者无相对滑动。已知斜面的倾角为θ,物体B的质量为m,则它们的加速度a及推力F的大小为( )
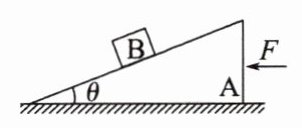
A. $a = g\sinθ$,$F = (μ + \sinθ)(M + m)g$
B. $a = g\cosθ$,$F = (M + m)g\cosθ$
C. $a = g\tanθ$,$F = (μ + \tanθ)(M + m)g$
D. $a = g\cosθ$,$F = μ(M + m)g$

A. $a = g\sinθ$,$F = (μ + \sinθ)(M + m)g$
B. $a = g\cosθ$,$F = (M + m)g\cosθ$
C. $a = g\tanθ$,$F = (μ + \tanθ)(M + m)g$
D. $a = g\cosθ$,$F = μ(M + m)g$
答案:
3.C解析:A与B一起向左做匀加速直线运动,合力水平向左,对B进行受力分析,B所受合力F合 = mgtanθ,根据牛顿第二定律得a = $\frac{F合}{m}$ = gtanθ,对A、B整体进行受力分析得F - μ(M + m)g = (M + m)a,解得F = (μ + tanθ)(M + m)g,故选项C正确。
4. 1966年人们曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验。实验时,用质量为$m_1$的双子星号宇宙飞船A去接触正在轨道上运行的质量为$m_2$的火箭组B(后者的发动机已熄火)。接触以后,开动双子星号飞船的推进器,使飞船和火箭组共同加速(如图所示)。推进器的平均推力F = 895N,推进器开动时间为7s,测出飞船和火箭组的速度变化量是0.91m/s。双子星号飞船的质量$m_1 = 3400kg$,求火箭组的质量$m_2$。(结果保留一位小数)
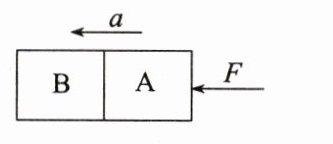

答案:
4.解析:对整体,由牛顿第二定律得F = (m₁ + m₂)a,由运动学公式得a = $\frac{Δv}{Δt}$ = 0.13m/s²,由以上两式得m₂ = 3484.6kg。
答案:3484.6kg
答案:3484.6kg
1. (2022·江苏卷)高铁车厢里的水平桌面上放置一本书,书与桌面间的动摩擦因数为0.4,最大静摩擦力等于滑动摩擦力,取g = 10m/s²。若书不滑动,则高铁的最大加速度不超过( )
A. 2.0m/s²
B. 4.0m/s²
C. 6.0m/s²
D. 8.0m/s²
A. 2.0m/s²
B. 4.0m/s²
C. 6.0m/s²
D. 8.0m/s²
答案:
1.B解析:书放在水平桌面上,若书相对于桌面不滑动,则最大静摩擦力提供加速度,即Fm = μmg = mam,解得am = μg = 4m/s²,书相对高铁静止,若书不动,高铁的最大加速度也为4m/s²。故选B。
2. 如图所示,a、b两个物体静止叠放在水平桌面上,已知$m_a = m_b = m$,a、b间的动摩擦因数为μ,b与地面间的动摩擦因数为$\frac{1}{4}μ$。已知最大静摩擦力等于滑动摩擦力,重力加速度为g。现对a施加一水平向右的拉力F,下列判断正确的是( )

A. 若a、b两个物体始终相对静止,则力F不能超过$\frac{3}{2}μmg$
B. 当力F = μmg时,a、b间的摩擦力为$\frac{3}{2}μmg$
C. 无论力F为何值,b的加速度不会超过$\frac{1}{4}μg$
D. 当力F>μmg时,b相对a滑动

A. 若a、b两个物体始终相对静止,则力F不能超过$\frac{3}{2}μmg$
B. 当力F = μmg时,a、b间的摩擦力为$\frac{3}{2}μmg$
C. 无论力F为何值,b的加速度不会超过$\frac{1}{4}μg$
D. 当力F>μmg时,b相对a滑动
答案:
2.A解析:a、b之间的最大静摩擦力为Ffmax = μmg,b与地面间的最大静摩擦力为Ffmax' = $\frac{1}{4}$μ(m + m)g = $\frac{1}{2}$μmg;a、b相对地面一起运动,刚好不发生相对滑动时,由牛顿第二定律,对b有μmg - $\frac{1}{2}$μmg = ma₀,得a₀ = $\frac{1}{2}$μg;对整体有F₀ - $\frac{1}{2}$μmg = 2ma₀,得F₀ = $\frac{3}{2}$μmg,所以若a、b两个物体始终相对静止,则力F不能超过$\frac{3}{2}$μmg,当力F>$\frac{3}{2}$μmg时,b相对a滑动,故A正确,D错误。当力F = μmg时,a、b一起加速运动,加速度为a₁ = $\frac{μmg - \frac{1}{2}μmg}{2m}$ = $\frac{1}{4}$μg,对a根据牛顿第二定律可得F - Fn = ma₁,解得a、b间的摩擦力为F = $\frac{3}{4}$μmg,故B错误。根据A、D选项的分析可知,无论力F为何值,b的加速度不会超过$\frac{1}{2}$μg,故C错误。
3. (多选)如图所示,在水平直轨道上的小车车厢内有一个倾角θ = 30°的光滑斜面,一细绳系着小球放在斜面上,细线与斜面平行。当小车以加速度a向左运动时( )

A. 若a = 20m/s²,小球受两个力的作用
B. 若a = 20m/s²,小球受三个力的作用
C. 若a = 10m/s²,小球受两个力的作用
D. 若a = 10m/s²,小球受三个力的作用

A. 若a = 20m/s²,小球受两个力的作用
B. 若a = 20m/s²,小球受三个力的作用
C. 若a = 10m/s²,小球受两个力的作用
D. 若a = 10m/s²,小球受三个力的作用
答案:
3.AD解析:设小车加速度为a₀时,小球刚好对斜面没有压力,以小球为对象,根据牛顿第二定律可得F合 = $\frac{mg}{tanθ}$ = ma₀,解得a₀ = gtanθ = gtan30° = $\frac{10\sqrt{3}}{3}$m/s²≈5.8m/s²,若a = 20m/s²,可知小球已经离开斜面,小球受到重力和细绳拉力两个力的作用,A正确,B错误;若a = 10m/s²,可知小球还没有离开斜面,小球受到重力、细绳拉力和斜面支持力三个力的作用,D正确,C错误。
4. 如图所示,质量为M = 4.0kg的一只铁箱A在水平拉力F作用下沿水平面向右运动,铁箱与水平面间的动摩擦因数为$μ_1 = 0.20$。这时铁箱内有一个质量为m = 1.0kg的木块B,木块与铁箱内壁间的动摩擦因数为$μ_2 = 0.40$。(取g = 10m/s²)

(1)求木块相对铁箱静止时受到铁箱内壁的摩擦力大小;
(2)要使A、B不发生相对滑动,水平拉力F至少多大?

(1)求木块相对铁箱静止时受到铁箱内壁的摩擦力大小;
(2)要使A、B不发生相对滑动,水平拉力F至少多大?
答案:
4.解析:
(1)对木块B进行受力分析,如图甲所示。

由图甲可知,木块相对铁箱静止时所受的摩擦力大小为Ff = mg = 1.0×10N = 10N。
(2)A、B之间不发生相对滑动的临界条件为A、B之间的静摩擦力达到最大静摩擦力。
对B受力分析可得FN = ma,Ff = mg,Ff = Ffmax = μ₂FN
代入数据可得a = 25m/s²。
对A、B整体进行受力分析,如图乙所示。

由图乙可知,根据牛顿第二定律有F - F滑 = (M + m)a,F滑 = μ₁FN,FN = (M + m)g。
代入数据解得F = 135N。
要使A、B不发生相对滑动,水平拉力至少为F = 135N。
答案:
(1)10N
(2)135N
4.解析:
(1)对木块B进行受力分析,如图甲所示。

由图甲可知,木块相对铁箱静止时所受的摩擦力大小为Ff = mg = 1.0×10N = 10N。
(2)A、B之间不发生相对滑动的临界条件为A、B之间的静摩擦力达到最大静摩擦力。
对B受力分析可得FN = ma,Ff = mg,Ff = Ffmax = μ₂FN
代入数据可得a = 25m/s²。
对A、B整体进行受力分析,如图乙所示。

由图乙可知,根据牛顿第二定律有F - F滑 = (M + m)a,F滑 = μ₁FN,FN = (M + m)g。
代入数据解得F = 135N。
要使A、B不发生相对滑动,水平拉力至少为F = 135N。
答案:
(1)10N
(2)135N
查看更多完整答案,请扫码查看


