第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
「实验目的」
1.会分析判断物体的运动性质,知道小车在重物牵引下速度随时间变化的规律。
2.能根据实验数据作出v−t图像,并能根据图像求加速度。
「实验器材」
________、一端带有滑轮的长木板、________、纸带、细绳、槽码、________、导线、交流电源、坐标纸等。
「实验步骤」
1.如图所示,把一端带有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,打点计时器固定在长木板没有滑轮的一端,连接好电路。
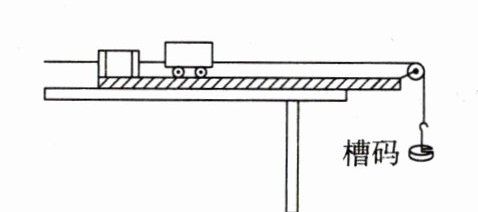
2.把小车停在________打点计时器的位置。
3.先启动计时器,然后________小车,在槽码的带动下,让它拖着纸带运动。打点计时器在________上打下一行小点。
4.________电源,取下纸带。
5.增减所挂的槽码(或在小车上放置重物),更换纸带,再做两次实验。
1.会分析判断物体的运动性质,知道小车在重物牵引下速度随时间变化的规律。
2.能根据实验数据作出v−t图像,并能根据图像求加速度。
「实验器材」
________、一端带有滑轮的长木板、________、纸带、细绳、槽码、________、导线、交流电源、坐标纸等。
「实验步骤」
1.如图所示,把一端带有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,打点计时器固定在长木板没有滑轮的一端,连接好电路。

2.把小车停在________打点计时器的位置。
3.先启动计时器,然后________小车,在槽码的带动下,让它拖着纸带运动。打点计时器在________上打下一行小点。
4.________电源,取下纸带。
5.增减所挂的槽码(或在小车上放置重物),更换纸带,再做两次实验。
答案:
打点计时器、小车、刻度尺
@@靠近
@@放开、纸带
@@关闭
@@靠近
@@放开、纸带
@@关闭
1.在“探究小车速度随时间变化的规律”的实验中:
(1)实验室提供了以下器材:电火花计时器、一端带有滑轮的长木板、小车、纸带、细绳、槽码、刻度尺、交流电源、停表、弹簧测力计。
其中在本实验中不需要的器材是________。
(2)实验中甲同学写出了如下实验步骤:
A.在桌面上放好长木板,在无滑轮的一端固定电火花计时器,用导线将电火花计时器接到8V的交流电源上。
B.将纸带固定在小车上,并使纸带穿过电火花计时器的限位孔。
C.用细绳的一端拴住小车,细绳的另一端跨过长木板上的定滑轮挂上槽码,将小车放在靠近电火花计时器一端的长木板上。
D.放开小车,让小车运动后再合上开关,使电火花计时器打点。
E.纸带全部通过后断开开关,取下纸带,测量和分析纸带。
乙同学检查了甲同学拟定的实验步骤,发现有两处错误。请你代乙同学纠正甲同学的错误:
错误1:______________________________;错误2:______________________________。
(1)实验室提供了以下器材:电火花计时器、一端带有滑轮的长木板、小车、纸带、细绳、槽码、刻度尺、交流电源、停表、弹簧测力计。
其中在本实验中不需要的器材是________。
(2)实验中甲同学写出了如下实验步骤:
A.在桌面上放好长木板,在无滑轮的一端固定电火花计时器,用导线将电火花计时器接到8V的交流电源上。
B.将纸带固定在小车上,并使纸带穿过电火花计时器的限位孔。
C.用细绳的一端拴住小车,细绳的另一端跨过长木板上的定滑轮挂上槽码,将小车放在靠近电火花计时器一端的长木板上。
D.放开小车,让小车运动后再合上开关,使电火花计时器打点。
E.纸带全部通过后断开开关,取下纸带,测量和分析纸带。
乙同学检查了甲同学拟定的实验步骤,发现有两处错误。请你代乙同学纠正甲同学的错误:
错误1:______________________________;错误2:______________________________。
答案:
(1)停表、弹簧测力计
(2)错误1:A中应将电火花计时器接到220V交流电源上。错误2:D中应先合上开关,再放开小车。
(1)停表、弹簧测力计
(2)错误1:A中应将电火花计时器接到220V交流电源上。错误2:D中应先合上开关,再放开小车。
2.在“探究小车速度随时间变化的规律”的实验中,下列做法不能减小实验误差的是( )
A.选取计数点,把每打5个点的时间间隔作为一个时间单位
B.分段测量各自距离
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的一部分进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
A.选取计数点,把每打5个点的时间间隔作为一个时间单位
B.分段测量各自距离
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的一部分进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
答案:
B
3.在“探究小车速度随时间变化的规律”的实验中,某同学利用纸带上的数据计算出了各计数点对应时刻小车的瞬时速度。然后她以速度v为纵轴、时间t为横轴建立直角坐标系,共描出了10个点,并“拟合”出了小车运动的v−t图像,如图所示。

针对该同学作出的v−t图像,她所在的实验小组的其他四位同学分别交流了自己的看法:
①这10个点无论如何也不在一条直线上,因此小车运动的图像不可能为一条直线,而应为一条平滑的曲线;
②这10个点中有8个点虽然不在一条直线上,但它们紧挨在该条直线附近,只有F和B两个点离这条直线远;
③在这10个点当中只有4个点(A、D、G、I)能画出一条直线上,其余6个点都不在该直线上,这条直线肯定不能表示小车的速度随时间变化的规律;
④与直线偏差较小的点(C、E、H、J)可能是实验误差造成的,而偏离直线较远的点(B、F)则可能是实验中出现失误造成的。
对于以上四种看法,你认为有道理的是( )
A.①③
B.②④
C.①②
D.③④

针对该同学作出的v−t图像,她所在的实验小组的其他四位同学分别交流了自己的看法:
①这10个点无论如何也不在一条直线上,因此小车运动的图像不可能为一条直线,而应为一条平滑的曲线;
②这10个点中有8个点虽然不在一条直线上,但它们紧挨在该条直线附近,只有F和B两个点离这条直线远;
③在这10个点当中只有4个点(A、D、G、I)能画出一条直线上,其余6个点都不在该直线上,这条直线肯定不能表示小车的速度随时间变化的规律;
④与直线偏差较小的点(C、E、H、J)可能是实验误差造成的,而偏离直线较远的点(B、F)则可能是实验中出现失误造成的。
对于以上四种看法,你认为有道理的是( )
A.①③
B.②④
C.①②
D.③④
答案:
B
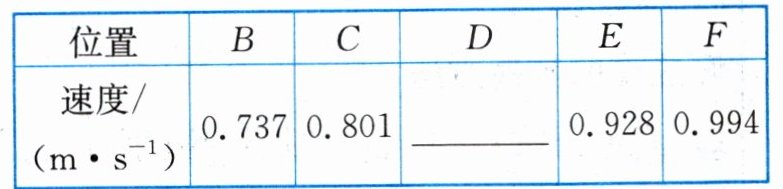
4.某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器得到的一条清晰纸带,如图所示。打点计时器打点的时间间隔T = 0.02s,将纸带上每隔4个点(图上没画出)按打点顺序依次标为A、B、C……其中x1 = 7.05cm、x2 = 7.68cm、x3 = 8.33cm、x4 = 8.95cm、x5 = 9.61cm、x6 = 10.26cm。

(1)下表列出了打点计时器打下B、C、E、F时小车的瞬时速度,请在表中填入打点计时器打下D点时小车的瞬时速度。
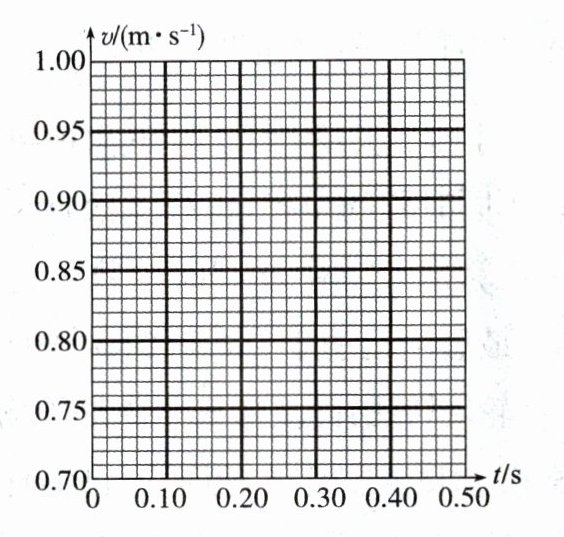
(2)以A点为计时起点,在坐标纸上画出小车的速度 - 时间关系图像。
(3)根据画出的小车的速度 - 时间关系图像计算出的小车的加速度a = ________m/s²,
方向是________(选填“A→B”或“B→A”)。

(1)下表列出了打点计时器打下B、C、E、F时小车的瞬时速度,请在表中填入打点计时器打下D点时小车的瞬时速度。

(2)以A点为计时起点,在坐标纸上画出小车的速度 - 时间关系图像。

(3)根据画出的小车的速度 - 时间关系图像计算出的小车的加速度a = ________m/s²,
方向是________(选填“A→B”或“B→A”)。
答案:
(1)0.864
(2)见解析图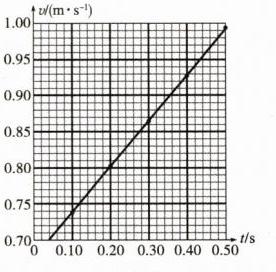
(3)0.64 B→A
(1)0.864
(2)见解析图

(3)0.64 B→A
5.光电计时器是物理学中常用的一种研究物体运动情况的计时仪器,其结构如图甲所示。a、b分别为光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示出物体的挡光时间,这样就可以将物体通过光电门的平均速度视为其通过光电门的瞬时速度。如图乙所示,气垫导轨上安装有A、B两个光电门,导轨上放有一滑块,滑块上装有宽度为d的遮光片。现使滑块从某一位置开始以恒定的加速度滑动,并依次通过光电门A、B,光电计时器记录的时间分别为t1、t2,并测得遮光片从光电门A运动到光电门B所用的时间△t。
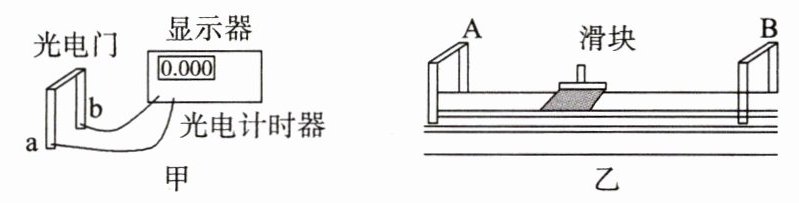
(1)在实验中,为了更准确地测得滑块通过光电门的瞬时速度,应选用较________(选填“宽”或“窄”)的遮光片。
(2)由题可知,遮光片通过光电门A的瞬时速度表达式v1 = ________,通过光电门B的瞬时速度表达式v2 = ________。
(3)滑块在气垫上运动的加速度的表达式a = ________(用v1、v2及题干中记录时间的字母表示)。

(1)在实验中,为了更准确地测得滑块通过光电门的瞬时速度,应选用较________(选填“宽”或“窄”)的遮光片。
(2)由题可知,遮光片通过光电门A的瞬时速度表达式v1 = ________,通过光电门B的瞬时速度表达式v2 = ________。
(3)滑块在气垫上运动的加速度的表达式a = ________(用v1、v2及题干中记录时间的字母表示)。
答案:
(1)窄
(2)$\frac{d}{t_1}$ $\frac{d}{t_2}$
(3)$\frac{v_2 - v_1}{\Delta t}$
(1)窄
(2)$\frac{d}{t_1}$ $\frac{d}{t_2}$
(3)$\frac{v_2 - v_1}{\Delta t}$
6.在“探究小车速度随时间变化的规律”的实验中,打点计时器接在50Hz的低压交流电源上,某同学在打出的纸带上每5个点取一个计数点,共取了A、B、C、D、E、F六个计数点,如图甲所示。从每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e),将这5段纸带由短到长紧靠、但不重叠地贴在Oxy坐标系中,如图乙所示,由此可以得到一条表示v−t关系的图线。
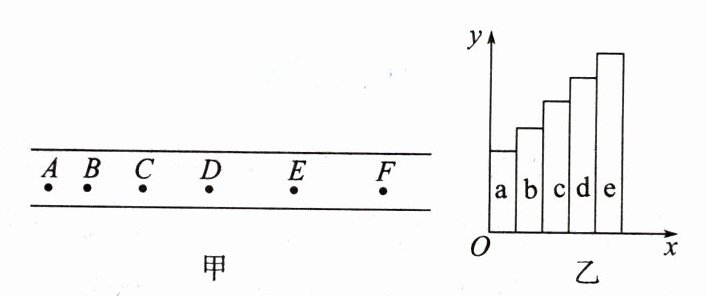
(1)请在图乙中用最简洁的方法作出能表示v−t关系的图线(画在图乙上),其________(选填“x”或“y”)轴相当于v轴。
(2)从第一个计数点开始计时,为求出t = 0.15s时刻的瞬时速度,需要测出________(选填“a、b、c、d、e”中的一个)段纸带的长度。
(3)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,则可求出加速度的大小为________m/s²。(结果保留一位小数)

(1)请在图乙中用最简洁的方法作出能表示v−t关系的图线(画在图乙上),其________(选填“x”或“y”)轴相当于v轴。
(2)从第一个计数点开始计时,为求出t = 0.15s时刻的瞬时速度,需要测出________(选填“a、b、c、d、e”中的一个)段纸带的长度。
(3)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,则可求出加速度的大小为________m/s²。(结果保留一位小数)
答案:
(1)见解析图 y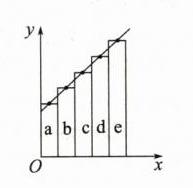
(2)b
(3)2.0
(1)见解析图 y

(2)b
(3)2.0
1. 定义及其分类

注意:匀变速直线运动是一种理想化模型。

注意:匀变速直线运动是一种理想化模型。
答案:
1. 加速度不变 均匀增加 均匀减小
2. 匀变速直线运动的v−t图像
(1) 匀变速直线运动的v−t图像是一条____的直线。
(2) 试判断下列图线表示哪种类型的匀变速直线运动,并说明理由。
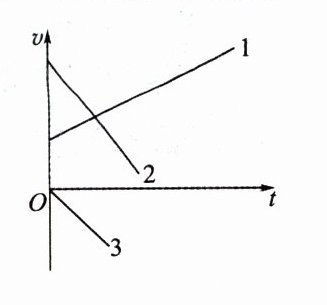
(1) 匀变速直线运动的v−t图像是一条____的直线。
(2) 试判断下列图线表示哪种类型的匀变速直线运动,并说明理由。

答案:
2.倾斜
@@提示:图线1表示匀加速直线运动,图线2表示匀减速直线运动,图线3表示反向的匀加速直线运动。
@@提示:图线1表示匀加速直线运动,图线2表示匀减速直线运动,图线3表示反向的匀加速直线运动。
1. 匀速直线运动的速度是恒定的,不随时间而改变。( )
2. 速度随时间不断增加的直线运动,一定是匀加速直线运动。( )
3. 在v−t图像中,只有图像的斜率与加速度有关。( )
4. 匀加速直线运动的v−t图像中,图线的斜率逐渐增大。( )
2. 速度随时间不断增加的直线运动,一定是匀加速直线运动。( )
3. 在v−t图像中,只有图像的斜率与加速度有关。( )
4. 匀加速直线运动的v−t图像中,图线的斜率逐渐增大。( )
答案:
√
@@×
@@√
@@×
@@×
@@√
@@×
1. 速度公式的推导
对于如图所示的v−t图像,你能从数学角度写出相应的函数表达式吗?分析表达式,图像在纵轴上的截距与图像的斜率分别表示什么意义?

对于如图所示的v−t图像,你能从数学角度写出相应的函数表达式吗?分析表达式,图像在纵轴上的截距与图像的斜率分别表示什么意义?

答案:
提示:由y = b + kx,得v = v₀ + at;图像在纵轴上的截距表示匀变速直线运动的初速度;图像的斜率表示匀变速直线运动的加速度。
[微训练]
1. 公式v = v₀ + at适用于任何做直线运动的物体。( )
2. 公式v = v₀ + at既适用于匀加速直线运动,也适用于匀减速直线运动。( )
1. 公式v = v₀ + at适用于任何做直线运动的物体。( )
2. 公式v = v₀ + at既适用于匀加速直线运动,也适用于匀减速直线运动。( )
答案:
×
@@√
@@√
[探究活动]
如图所示的是A、B两物体做匀变速直线运动的速度一时间图像。
(1)A、B各做什么运动?其加速度是多少?(2)两图线的交点有什么物理意义?
如图所示的是A、B两物体做匀变速直线运动的速度一时间图像。

(1)A、B各做什么运动?其加速度是多少?(2)两图线的交点有什么物理意义?
答案:
解:
(1)物体A沿规定的正方向做匀加速直线运动,
加速度a₁ =$ \frac{v_{t}-v_{0}}{t}$=$\frac{8 - 2}{6}m/s² $= 1 m/s²,方向与规定的正方向相同;
物体B前4 s沿规定的正方向做匀减速直线运动,4 s后沿反方向做匀加速直线运动,
其加速度a₂ =$ \frac{v_{t}'-v_{0}'}{t'}$=$\frac{-4 - 8}{6}m/s²$ = - 2 m/s²,负号表示与规定的正方向相反。
(2)两图线的交点表示二者在t = 2 s时速度相同。
(1)物体A沿规定的正方向做匀加速直线运动,
加速度a₁ =$ \frac{v_{t}-v_{0}}{t}$=$\frac{8 - 2}{6}m/s² $= 1 m/s²,方向与规定的正方向相同;
物体B前4 s沿规定的正方向做匀减速直线运动,4 s后沿反方向做匀加速直线运动,
其加速度a₂ =$ \frac{v_{t}'-v_{0}'}{t'}$=$\frac{-4 - 8}{6}m/s²$ = - 2 m/s²,负号表示与规定的正方向相反。
(2)两图线的交点表示二者在t = 2 s时速度相同。
1. (多选) 一物体做直线运动,下列选项中表示该物体做匀变速直线运动的是( )


答案:
AC 解析:v - t图像的斜率保持不变,说明加速度恒定不变,物体做匀变速直线运动,故A正确;x - t图像的斜率保持不变,说明运动速度恒定不变,物体做匀速直线运动,故B错误;a - t图像的纵坐标保持不变,说明物体的加速度不变,物体做匀变速直线运动,故C正确;v - t图像的斜率不断变化,说明物体做加速度变化的直线运动,故D错误。
2. 某物体沿水平方向做直线运动,其v−t图像如图所示,规定向右为正方向,下列判断正确的是( )

A. 在0~1s内,物体的加速度逐渐增大
B. 在1~2s内,物体向左运动,且速度的大小在减小
C. 在1~3s内,物体的加速度方向向左,大小为4m/s²
D. 在1~3s内,物体的速度始终在减小

A. 在0~1s内,物体的加速度逐渐增大
B. 在1~2s内,物体向左运动,且速度的大小在减小
C. 在1~3s内,物体的加速度方向向左,大小为4m/s²
D. 在1~3s内,物体的速度始终在减小
答案:
C 解析:在0~1s内,物体做加速度减小而速度增大的直线运动,A错误;在1~2s内,物体的速度为正,表示物体向右运动,斜率为负,表示加速度与初速度方向相反,物体做减速运动,B错误;在1~3s内,物体的加速度a = $\frac{v - v₀}{t}$ = $\frac{-4 - 4}{2}$ m/s² = -4 m/s²,可知加速度方向向左,C正确;在1~3s内,物体的速度先减小后反向增大,D错误。
3. (多选) 如图所示的为物体A、B从同地点沿同一直线动的部分v−t图关于两物体在0~3s内的运动,下列判断正确的是( )

A. 物体A和B的运动方向相同
B. 物体B的加速度大小为2m/s²
C. t = 3s时,物体A、B的速度相同
D. t = 3s时,物体A、B之间的距离最大

A. 物体A和B的运动方向相同
B. 物体B的加速度大小为2m/s²
C. t = 3s时,物体A、B的速度相同
D. t = 3s时,物体A、B之间的距离最大
答案:
ACD 解析:A、B两物体的速度均为正值,因此运动方向相同,A正确;在v - t图像中,图线的斜率表示加速度,因此物体B的加速度大小aB = $\frac{Δv}{Δt}$ = $\frac{10}{3}$ m/s²,B错误;t = 3s时,物体A、B的速度相同,且均为10m/s,C正确;达到相同的速度之前A的速度一直比B的速度大,直到速度相同时两者之间的距离最大,因此t = 3s时,物体A、B之间的距离最大,D正确。
4. 如图甲所示的“冰爬犁”是北方儿童在冬天的一种游戏用具:“上坐一人,双手握冰钎子,向后下方用力点冰,则冰床前进如飞。”在空旷的水平冰面上,有一小孩从静止开始,连续三次“点冰”后,冰爬犁沿直线继续滑行最后停下。某同学用v−t图像描述了上述运动过程,如图乙所示,图中OA//BC//DE,AB//CD//EF。
(1) 求冰爬犁加速时的加速度大小。
(2) 冰爬犁运动的最大速度为多少?


(1) 求冰爬犁加速时的加速度大小。
(2) 冰爬犁运动的最大速度为多少?


答案:
解析:
(1)冰爬犁加速时的加速度为a₁ = $\frac{v_A}{t_A}$ = 1.25 m/s²。
(2)AB段的加速度为a₂ = $\frac{v_B - v_A}{t_B - t_A}$ = -$\frac{1}{6}$ m/s²。
由题图乙可知,从0~4.8s内,加速共用时2.4s,减速共用时2.4s,又OA//BC//DE,AB//CD//EF,则加速阶段加速度相同,减速阶段加速度也相同,则冰爬犁运动的最大速度为vₘ = a₁×2.4s + a₂×2.4s = 2.6 m/s。
答案:
(1)1.25 m/s²
(2)2.6 m/s
(1)冰爬犁加速时的加速度为a₁ = $\frac{v_A}{t_A}$ = 1.25 m/s²。
(2)AB段的加速度为a₂ = $\frac{v_B - v_A}{t_B - t_A}$ = -$\frac{1}{6}$ m/s²。
由题图乙可知,从0~4.8s内,加速共用时2.4s,减速共用时2.4s,又OA//BC//DE,AB//CD//EF,则加速阶段加速度相同,减速阶段加速度也相同,则冰爬犁运动的最大速度为vₘ = a₁×2.4s + a₂×2.4s = 2.6 m/s。
答案:
(1)1.25 m/s²
(2)2.6 m/s
1. 一物体做匀加速直线运动,已知第1s末的速度是6m/s,第2s末的速度是8m/s,则下列结论不正确的是( )
A. 该物体在t = 0时刻的速度是4m/s
B. 该物体的加速度是2m/s²
C. 任何1s内的速度变化量都是2m/s
D. 每1s初的速度比前1s末的速度大2m/s
A. 该物体在t = 0时刻的速度是4m/s
B. 该物体的加速度是2m/s²
C. 任何1s内的速度变化量都是2m/s
D. 每1s初的速度比前1s末的速度大2m/s
答案:
D 解析:该物体的加速度a = $\frac{v_2 - v_1}{t_2 - t_1}$ = $\frac{8 - 6}{1}$ m/s² = 2 m/s²,设t = 0时刻速度为v₀,则由v₁ = v₀ + at₁得v₀ = v₁ - at₁ = (6 - 2×1) m/s = 4 m/s,故A、B正确。由Δv = at可得任何1s内的速度变化量均为2 m/s,故C正确。每1s初与前1s末是同一个时刻,速度相同,故D错误。
2. 一学生在玩遥控直升机,通过遥控控制直升机从地面开始做竖直向上的匀加速直线运动,加速6s后直升机的速度达到30m/s,此时撤去遥控控制,直升机随即做向上的匀减速直线运动,加速度大小为10m/s²,下列说法正确的是( )

A. 加速上升时,直升机的加速度大小为2.5m/s²
B. 加速上升时,直升机的加速度方向竖直向下
C. 减速上升时,直升机的加速度方向竖直向上
D. 直升机减速上升的时间为3s

A. 加速上升时,直升机的加速度大小为2.5m/s²
B. 加速上升时,直升机的加速度方向竖直向下
C. 减速上升时,直升机的加速度方向竖直向上
D. 直升机减速上升的时间为3s
答案:
D 解析:加速上升时,直升机的加速度大小为a = $\frac{v}{t}$ = $\frac{30}{6}$ m/s² = 5 m/s²,加速度和速度同向,则直升机的加速度方向竖直向上,A、B错误;减速上升时,加速度和速度方向相反,则直升机的加速度方向竖直向下,直升机减速上升的时间为t = $\frac{v}{a}$ = $\frac{30}{10}$ s = 3 s,C错误,D正确。
3. (2022·全国甲卷) 长为l的高速列车在平直轨道上正常行驶,速率为v₀,要通过前方一长为L的隧道,当列车的任一部分处于隧道内时,列车速率都不允许超过v(v<v₀)。已知列车加速和减速时加速度的大小分别为a和2a,则列车从减速开始至回到正常行驶速率v₀所用时间至少为( )
A. $\frac{v₀ - v}{2a}$ + $\frac{L + l}{v}$
B. $\frac{v₀ - v}{a}$ + $\frac{L + l}{v}$
C. $\frac{3(v₀ - v)}{2a}$ + $\frac{L + l}{v}$
D. $\frac{3(v₀ - v)}{a}$ + $\frac{L + l}{v}$
A. $\frac{v₀ - v}{2a}$ + $\frac{L + l}{v}$
B. $\frac{v₀ - v}{a}$ + $\frac{L + l}{v}$
C. $\frac{3(v₀ - v)}{2a}$ + $\frac{L + l}{v}$
D. $\frac{3(v₀ - v)}{a}$ + $\frac{L + l}{v}$
答案:
C 解析:由题知当列车的任一部分处于隧道内时,列车速率都不允许超过v(v<v₀),则列车进隧道前至少减速到v,有v = v₀ - at₁,解得t₁ = $\frac{v₀ - v}{a}$,在隧道内匀速行驶,有t₂ = $\frac{L + l}{v}$,列车尾部出隧道后立即加速到v₀,有v₀ = v + at₃,解得t₃ = $\frac{v₀ - v}{a}$,则列车从减速开始至回到正常行驶速率v₀所用最少时间为t = $\frac{2(v₀ - v)}{a}$ + $\frac{L + l}{v}$,故选C。
一辆汽车以45km/h的速度匀速行驶。
(1) 若汽车以0.6m/s²的加速度加速,则10s后速度能达到多少?
(2) 若汽车刹车时以0.6m/s²的加速度减速,则10s后速度能达到多少?
(3) 若汽车刹车时以3m/s²的加速度减速,则10s后速度为多少?
(1) 若汽车以0.6m/s²的加速度加速,则10s后速度能达到多少?
(2) 若汽车刹车时以0.6m/s²的加速度减速,则10s后速度能达到多少?
(3) 若汽车刹车时以3m/s²的加速度减速,则10s后速度为多少?
答案:
提示:
(1)已知汽车初速度v₀ = 45 km/h = 12.5 m/s,加速度a = 0.6 m/s²,时间t = 10 s,10s后汽车的速度为v = v₀ + at = 12.5 m/s + 0.6×10 m/s = 18.5 m/s。
(2)已知刹车时a₁ = -0.6 m/s²,刹车所用时间为t₁ = $\frac{0 - v₀}{a₁}$ = $\frac{0 - 12.5}{-0.6}$ s ≈ 20.83 s>10 s,所以10s后汽车的速度为v = v₀ + a₁t = 12.5 m/s - 0.6×10 m/s = 6.5 m/s。
(3)已知刹车时a₂ = -3 m/s²,汽车刹车所用时间为t₂ = $\frac{0 - v₀}{a₂}$ = $\frac{0 - 12.5}{-3}$ s ≈ 4.17 s<10 s,所以10s后汽车已经刹车完毕,则10s后汽车速度为0。
(1)已知汽车初速度v₀ = 45 km/h = 12.5 m/s,加速度a = 0.6 m/s²,时间t = 10 s,10s后汽车的速度为v = v₀ + at = 12.5 m/s + 0.6×10 m/s = 18.5 m/s。
(2)已知刹车时a₁ = -0.6 m/s²,刹车所用时间为t₁ = $\frac{0 - v₀}{a₁}$ = $\frac{0 - 12.5}{-0.6}$ s ≈ 20.83 s>10 s,所以10s后汽车的速度为v = v₀ + a₁t = 12.5 m/s - 0.6×10 m/s = 6.5 m/s。
(3)已知刹车时a₂ = -3 m/s²,汽车刹车所用时间为t₂ = $\frac{0 - v₀}{a₂}$ = $\frac{0 - 12.5}{-3}$ s ≈ 4.17 s<10 s,所以10s后汽车已经刹车完毕,则10s后汽车速度为0。
1. 以10m/s的速度匀速行驶的汽车,刹车后做匀减速直线运动,加速度大小为3m/s²,则汽车刹车后第3s末的速度大小为( )
A. 2.0m/s
B. 1.0m/s
C. 0
D. - 1.0m/s
A. 2.0m/s
B. 1.0m/s
C. 0
D. - 1.0m/s
答案:
B 解析:由速度公式可得v = v₀ - at = 1.0 m/s,第3s末仍未停止,故第3s末的速度大小为1.0 m/s,B正确。
2. (多选) 如图所示,物体以10m/s的初速度冲上光滑斜面,已知物体在斜面上运动的加速度大小始终为5m/s²,方向沿斜面向下,当物体速度大小变为5m/s时,经历的时间可能为( )

A. 1s
B. 2s
C. 3s
D. 4s

A. 1s
B. 2s
C. 3s
D. 4s
答案:
AC 解析:选沿斜面向上为正方向,若5 m/s的速度沿斜面向上,则5 = 10 - 5t,得t = 1 s,若5 m/s的速度沿斜面向下,则 -5 = 10 - 5t,得t = 3 s,故选A、C。
3. 卡车原来用10m/s的速度在平直公路上匀速行驶,因为道口出现红灯,司机从较远的地方开始刹车,使卡车匀减速前进,当卡车减速到2m/s时,交通灯转为绿灯,司机当即放开刹车,并且只用了减速过程的一半时间卡车就加速到原来的速度,从开始刹车到恢复原速历时12s。求:
(1) 减速与加速过程中的加速度;
(2) 开始刹车后2s末及10s末的瞬时速度。
(1) 减速与加速过程中的加速度;
(2) 开始刹车后2s末及10s末的瞬时速度。
答案:
解析:
(1)卡车先做匀减速直线运动,再做匀加速直线运动,其运动简图如图所示,设卡车从A点开始减速,则vA = 10 m/s,经过时间t₁到达B点,从B点又开始加速,经过时间t₂到达C点,由题意可知vB = 2 m/s,vC = 10 m/s,且t₂ = $\frac{1}{2}$t₁,t₁ + t₂ = 12 s。
解得t₁ = 8 s,t₂ = 4 s。
由v = v₀ + at得,在AB段,vB = vA + a₁t₁,在BC段,vC = vB + a₂t₂。
联立解得a₁ = -1 m/s²,a₂ = 2 m/s²。
(2)开始刹车后,2s末的速度为v₁ = vA + a₁t' = 10 m/s - 1×2 m/s = 8 m/s;
10s末的速度为v₂ = vB + a₂t'' = 2 m/s + 2×(10 - 8) m/s = 6 m/s。
答案:
(1)1 m/s²,方向与初速度方向相反;2 m/s²,方向与初速度方向相同
(2)8 m/s,方向与初速度方向相同;6 m/s,方向与初速度方向相同
(1)卡车先做匀减速直线运动,再做匀加速直线运动,其运动简图如图所示,设卡车从A点开始减速,则vA = 10 m/s,经过时间t₁到达B点,从B点又开始加速,经过时间t₂到达C点,由题意可知vB = 2 m/s,vC = 10 m/s,且t₂ = $\frac{1}{2}$t₁,t₁ + t₂ = 12 s。
解得t₁ = 8 s,t₂ = 4 s。
由v = v₀ + at得,在AB段,vB = vA + a₁t₁,在BC段,vC = vB + a₂t₂。
联立解得a₁ = -1 m/s²,a₂ = 2 m/s²。
(2)开始刹车后,2s末的速度为v₁ = vA + a₁t' = 10 m/s - 1×2 m/s = 8 m/s;
10s末的速度为v₂ = vB + a₂t'' = 2 m/s + 2×(10 - 8) m/s = 6 m/s。
答案:
(1)1 m/s²,方向与初速度方向相反;2 m/s²,方向与初速度方向相同
(2)8 m/s,方向与初速度方向相同;6 m/s,方向与初速度方向相同
1.(1)匀变速直线运动位移公式的推导

匀速直线运动的−t图像中,速度与时间的______表示位移。

匀变速直线运动的u−t图像中,将物体的运动分成数段;无限分下去,小矩形合在一起近似成________运动的图像(一个梯形)。

v−t图像中,图线与横轴围成梯形的面积表示物体运动的位移x。
(2)如图所示的是某物体做匀变速直线运动的v−t图像,其位移大小可以用梯形部分的面积表示,用图中符号可表示为x=________。
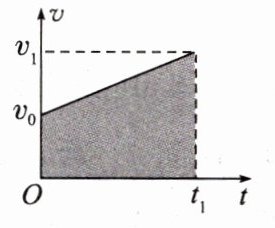

匀速直线运动的−t图像中,速度与时间的______表示位移。

匀变速直线运动的u−t图像中,将物体的运动分成数段;无限分下去,小矩形合在一起近似成________运动的图像(一个梯形)。

v−t图像中,图线与横轴围成梯形的面积表示物体运动的位移x。
(2)如图所示的是某物体做匀变速直线运动的v−t图像,其位移大小可以用梯形部分的面积表示,用图中符号可表示为x=________。

答案:
乘积 匀变速直线 $\frac{1}{2}$(v₀ + v₁)t₁
2.位移与时间的关系式
(1)将v=v+at代入x=$\frac{1}{2}$(v0+v)t,可得位移与时间的关系式x=________。
(2)在x−t图像中匀变速直线运动的图线是____________的一部分。
(3)若vo=0,关系式为x=________(由静止开始的匀变速直线运动)。
(1)将v=v+at代入x=$\frac{1}{2}$(v0+v)t,可得位移与时间的关系式x=________。
(2)在x−t图像中匀变速直线运动的图线是____________的一部分。
(3)若vo=0,关系式为x=________(由静止开始的匀变速直线运动)。
答案:
(1)v₀t + $\frac{1}{2}$at²
(2)抛物线
(3)$\frac{1}{2}$at²
(1)v₀t + $\frac{1}{2}$at²
(2)抛物线
(3)$\frac{1}{2}$at²
[微训练]
根据预习内容判断以下说法正误。
1.匀变速直线运动的位移与时间的平方一定成正比。 ( )
2.初速度越大,做匀变速直线运动的物体的位移一定越大。 ( )
3.匀变速直线运动的位移与初速度、加速度、时间三个因素有关。 ( )
根据预习内容判断以下说法正误。
1.匀变速直线运动的位移与时间的平方一定成正比。 ( )
2.初速度越大,做匀变速直线运动的物体的位移一定越大。 ( )
3.匀变速直线运动的位移与初速度、加速度、时间三个因素有关。 ( )
答案:
1.× 2.× 3.√
1.关系式的推导过程:由匀变速直线运动的速度公式v=v0+at和匀变速直线运动的位移公式x=vot+$\frac{1}{2}$at²相结合,消去________而得。
答案:
时间t
2.速度与位移的关系式:v²−v²=________。若v0=0(由静止开始的匀变速直线运动),则关系式变为________。
答案:
2ax v² = 2ax
3.当问题的已知量和未知量都不涉及________时,利用v²−v²=2ax求解,往往会使问题任务一对匀变速直线运动中位移与时间关系式的理解
答案:
时间t
[探究活动]
如图所示,汽车由静止以加速度a1加速启动,行驶一段时间t1后,又以加速度a2减速刹车,经时间t2后停下来。
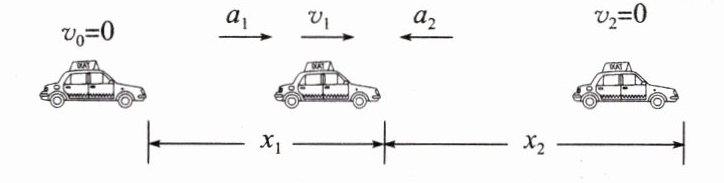
(1)在汽车加速过程与减速过程中,加速度的方向相同吗?
(2)根据位移与时间关系式求加速过程及减速过程中的位移时,初速度和加速度的正负如何确定?
如图所示,汽车由静止以加速度a1加速启动,行驶一段时间t1后,又以加速度a2减速刹车,经时间t2后停下来。

(1)在汽车加速过程与减速过程中,加速度的方向相同吗?
(2)根据位移与时间关系式求加速过程及减速过程中的位移时,初速度和加速度的正负如何确定?
答案:
(1)汽车加速时加速度的方向与运动方向相同,减速时加速度的方向与运动方向相反,因此两过程中汽车的加速度方向不相同。
(2)根据位移与时间关系式求位移时,如果取初速度方向为正方向,加速过程中,加速度取正值,减速过程中,加速度取负值。
(1)汽车加速时加速度的方向与运动方向相同,减速时加速度的方向与运动方向相反,因此两过程中汽车的加速度方向不相同。
(2)根据位移与时间关系式求位移时,如果取初速度方向为正方向,加速过程中,加速度取正值,减速过程中,加速度取负值。
[微训练]
根据预习内容判断以下说法正误。
1.公式v0²−v²=2ax适用于任何直线运动。
( )
2.物体的末速度越大,位移越大。 ( )
3.对匀减速直线运动,公式v²−v²=2ax中的a必须取负值。 ( )
根据预习内容判断以下说法正误。
1.公式v0²−v²=2ax适用于任何直线运动。
( )
2.物体的末速度越大,位移越大。 ( )
3.对匀减速直线运动,公式v²−v²=2ax中的a必须取负值。 ( )
答案:
1.× 2.× 3.×
1.一物体做匀变速直线运动,下列说法正确的是 ( )
A.物体的末速度一定与时间成正比
B.物体的位移一定与时间的二次方成正比
C.物体的速度在一段时间内发生的变化与这段时间成正比
D.若为匀速运动,速度与位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
A.物体的末速度一定与时间成正比
B.物体的位移一定与时间的二次方成正比
C.物体的速度在一段时间内发生的变化与这段时间成正比
D.若为匀速运动,速度与位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
答案:
C 解析:根据v₁ = v₀ + at和x = v₀t + $\frac{1}{2}$at² 可知,若物体的初速度v₀不为0,A、B错误;由a = $\frac{\Delta v}{\Delta t}$可知,Δv = aΔt,a不变时,Δv与Δt成正比,C正确;当物体做匀减速运动时,速度减小但位移可以增大,D错误。
2.(多选)冰壶运动,又称掷冰壶、冰上溜石,是以队为单位在冰上进行的一种投掷性竞赛项目,属冬奥会比赛项目,并设有冰壶世锦赛。在某次比赛中,冰壶被投出后,假设其做匀减速直线运动,用时20s停止,最后1s 内其位移大小为0.2m,则下列说法正确的是 ( )
A.冰壶的加速度大小是0.3m/s²
B.冰壶的加速度大小是0.4m/s²
C.冰壶第1s内的位移大小是7.8m
D.冰壶的初速度大小是6m/s
A.冰壶的加速度大小是0.3m/s²
B.冰壶的加速度大小是0.4m/s²
C.冰壶第1s内的位移大小是7.8m
D.冰壶的初速度大小是6m/s
答案:
BC 解析:冰壶匀减速直线运动的逆过程是初速度为0的匀加速直线运动,最后1s内的位移为0.2m,根据位移与时间关系式x₁ = $\frac{1}{2}$at²,代入数据解得a = 0.4m/s²,故B正确,A错误;初速度v₀ = at = 0.4×20m/s = 8m/s,冰壶第1s内的位移大小为x₁ = v₀t - $\frac{1}{2}$at² = 8×1m - $\frac{1}{2}$×0.4×1²m = 7.8m,故C正确,D错误。
3.一质点做匀变速直线运动,其位移表达式为x=(10t−t²)m,则 ( )
A质点的初速度为10m/s
B.质点的加速度大小为1m/s²
C.质点2s末的速度是12m/s
D.在5s末,质点回到出发点
A质点的初速度为10m/s
B.质点的加速度大小为1m/s²
C.质点2s末的速度是12m/s
D.在5s末,质点回到出发点
答案:
A 解析:匀变速直线运动的位移公式为x = v₀t + $\frac{1}{2}$at²,对比题中表达式可知v₀ = 10m/s,a = -2m/s²,且10s末,质点回到出发点,A正确,B、D错误;质点2s末的速度为v = (10 - 2×2)m/s = 6m/s,C错误。
4.(2022.河北卷)科学训练可以提升运动成绩,某短跑运动员科学训练前、后百米全程测试中,速度v与时间t的关系图像如图所示。由图像可知 ( )

A.0~t1时间内,训练后运动员的平均加速度大
B.0~t2时间内,训练前、后运动员跑过的距离相等
C.t2~t3时间内,训练后运动员的平均速度小
D.t3时刻后,运动员训练前做减速运动,训练后做加速运动

A.0~t1时间内,训练后运动员的平均加速度大
B.0~t2时间内,训练前、后运动员跑过的距离相等
C.t2~t3时间内,训练后运动员的平均速度小
D.t3时刻后,运动员训练前做减速运动,训练后做加速运动
答案:
D 解析:根据v - t图像的斜率表示加速度,由题图可知0 - t₁时间内,训练后运动员的平均加速度比训练前的小,故A错误;根据v - t图像围成图形的面积表示位移,由题图可知0~t₂时间内,训练前运动员跑过的距离比训练后的大,故B错误;由题图可知t₂~t₃时间内,训练后运动员的位移比训练前的位移大,根据平均速度等于位移与时间的比值,可知训练后运动员的平均速度大,故C错误;根据v - t图像可直接判断出,t₃时刻后,运动员训练前速度减小,做减速运动,运动员训练后速度增加,做加速运动,故D正确。
5.质点从静止开始做匀加速直线运动,在第1个2s、第2个2s和第5个2s内三段位移之比为 ( )
A.1:4:25 B.2:8:17
C.1:3:9 D.2:2:1
A.1:4:25 B.2:8:17
C.1:3:9 D.2:2:1
答案:
C 解析:根据x = $\frac{1}{2}$at²知,物体在T内、2T内、3T内……nT内的位移之比为1:4:9:……:n²,则第1个T内、第2个T内、第5个T内的位移之比为1:3:9,故选C。
1.如图所示,某国产品牌汽车装备了具有“全力自动刹车”功能的城市安全系统,系统以50Hz的频率监视前方的交通状况。当车速v≤10m/s且与前方静止的障碍物之间的距离接近安全距离时,如果司机未采取制动措施,系统就会立即启动“全力自动刹车”功能,此时加速度大小约为4m/s²,避免汽车与障碍物相撞。则“全力自动刹车”系统设置的安全距离约为 ( )

A.40m B 25m
C.12.5m D.2m

A.40m B 25m
C.12.5m D.2m
答案:
1.C 解析:由题意知,可以避免汽车与静止的障碍物相撞的安全距离为汽车以4m/s²的加速度由v = 10m/s减速至静止过程中位移的大小,由0 - v² = 2ax可得x = $\frac{-v²}{2a}$ = $\frac{-10²}{2×(-4)}$m = 12.5m,所以系统设置的安全距离约为12.5m,故C正确,A、B、D错误。
2.某同学在滑冰时,先后两次以不同的初速度沿同一水平冰面滑出,滑出后做匀减速直线运动,滑行不同距离后停下。若该同学第一次与第二次滑出的初速度大小之比为k,则他第一次与第二次滑行的距离之比为 ( )
A.$\frac{1}{k}$ B.k
C. $\sqrt{k}$ D.k²
A.$\frac{1}{k}$ B.k
C. $\sqrt{k}$ D.k²
答案:
2.D 解析:设两次滑出的初速度大小分别为v₁、v₂,两次滑行距离分别为x₁、x₂,而且加速度大小相等,依题意有v₁² = 2ax₁,v₂² = 2ax₂,因v₁:v₂ = k,则可得x₁:x₂ = k²,故选D。
3.党的二十大开幕会提出“促进群众体育和竞技体育全面发展,加快建设体育强国”,为响应号召,重庆外国语学校在大课间安排学生在操场折返跑。如图所示,A、B为跑道两个端点,学生们排成一列纵队在A、B间沿直线跑动,到端点后折返。某次跑步中,所有学生依次从A端出发,均以1.5m/s²的加速度匀加速运动,达到3m/s后做一段匀速运动,之后以1m/s²的加速度匀减速运动,到达B端时速度刚好为0,之后反向,重复之前由A到B的运动过程,循环多次,每次经过端点时速度均为0。已知A、B间距离为L=43.5m,匀速运动阶段相邻两同学间的距离为d=1m,学生可看作质点,往返跑道间距离足够小。
(1)求每个学生跑完一个往返需要的时间t;
(2)某个班级共50名同学参加跑步,当第1 名同学跑回到A点时,求第50名同学与B 点的距离x。\

(1)求每个学生跑完一个往返需要的时间t;
(2)某个班级共50名同学参加跑步,当第1 名同学跑回到A点时,求第50名同学与B 点的距离x。\

答案:
解析:
(1)任取一个学生为研究对象,在从某端点开始加速时,由运动学公式有x₁ = $\frac{v²}{2a}$ = $\frac{3²}{2×1.5}$m = 3m,t₁ = $\frac{v}{a}$ = $\frac{3}{1.5}$s = 2s。
该同学到达另一端点做匀减速直线运动,由运动学公式有x₂ = $\frac{v²}{2a₂}$ = $\frac{3²}{2×1}$m = 4.5m,t₂ = $\frac{v}{a₂}$ = 3s。
该同学做匀速运动的时间为t₃ = $\frac{L - x₁ - x₂}{v}$ = $\frac{43.5 - 3 - 4.5}{3}$s = 12s,该段时间内跑过的距离为x₃ = vt₃ = 3×12m = 36m。
该同学往返一次所用的总时间为t = 2(t₁ + t₂ + t₃) = 34s。
(2)匀速运动阶段,相邻两同学间的距离为d = 1m,相邻两位同学起跑的先后时间差为t₀ = $\frac{d}{v}$ = $\frac{1}{3}$s。
当第一位同学返回端点A时,最后一位同学落后他的时间差为t₄ = (n - 1)t₀ = (50 - 1)×$\frac{1}{3}$s = $\frac{49}{3}$s,即第50位同学还需要t₄ = $\frac{49}{3}$s返回端点A。在他返回端点A时,减速需要时间3s,匀速经过中间的36m需要时间12s,因此在离开B点加速到v₁还需要再加速t₅速度达到3m/s,则t₅ = t₄ - t₂ - t₃ = $\frac{49}{3}$s - 3s - 12s = $\frac{4}{3}$s。
此时该同学速度为v₁ = v - a₁t₅ = 3m/s - 1.5×$\frac{4}{3}$s = 1m/s,所以从B端点加速到该速度,所经过的位移为x = $\frac{v₁²}{2a}$ = $\frac{1²}{2×1.5}$m = $\frac{1}{3}$m。
第50名同学与B点的距离s为$\frac{1}{3}$m。
答案:
(1)34s
(2)$\frac{1}{3}$m
(1)任取一个学生为研究对象,在从某端点开始加速时,由运动学公式有x₁ = $\frac{v²}{2a}$ = $\frac{3²}{2×1.5}$m = 3m,t₁ = $\frac{v}{a}$ = $\frac{3}{1.5}$s = 2s。
该同学到达另一端点做匀减速直线运动,由运动学公式有x₂ = $\frac{v²}{2a₂}$ = $\frac{3²}{2×1}$m = 4.5m,t₂ = $\frac{v}{a₂}$ = 3s。
该同学做匀速运动的时间为t₃ = $\frac{L - x₁ - x₂}{v}$ = $\frac{43.5 - 3 - 4.5}{3}$s = 12s,该段时间内跑过的距离为x₃ = vt₃ = 3×12m = 36m。
该同学往返一次所用的总时间为t = 2(t₁ + t₂ + t₃) = 34s。
(2)匀速运动阶段,相邻两同学间的距离为d = 1m,相邻两位同学起跑的先后时间差为t₀ = $\frac{d}{v}$ = $\frac{1}{3}$s。
当第一位同学返回端点A时,最后一位同学落后他的时间差为t₄ = (n - 1)t₀ = (50 - 1)×$\frac{1}{3}$s = $\frac{49}{3}$s,即第50位同学还需要t₄ = $\frac{49}{3}$s返回端点A。在他返回端点A时,减速需要时间3s,匀速经过中间的36m需要时间12s,因此在离开B点加速到v₁还需要再加速t₅速度达到3m/s,则t₅ = t₄ - t₂ - t₃ = $\frac{49}{3}$s - 3s - 12s = $\frac{4}{3}$s。
此时该同学速度为v₁ = v - a₁t₅ = 3m/s - 1.5×$\frac{4}{3}$s = 1m/s,所以从B端点加速到该速度,所经过的位移为x = $\frac{v₁²}{2a}$ = $\frac{1²}{2×1.5}$m = $\frac{1}{3}$m。
第50名同学与B点的距离s为$\frac{1}{3}$m。
答案:
(1)34s
(2)$\frac{1}{3}$m
任务三平均速度、中间时刻的速度与中间位置的速度
[探究活动]
2022年1月10日,京港高铁赣州至深圳段开通运营“满月”。一个月以来,该路段高铁为旅客提供了更为便捷、舒适的乘车体验,共计发送旅客22万人次。如图所示的为高铁列车从赣州车站出站后一段位移内的v−t图像。
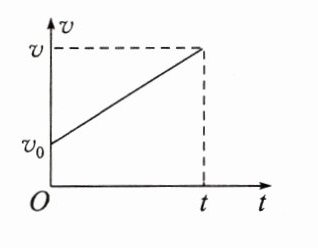
(1)试通过v−t图像求出列车出站$\frac{t}{2}$时刻的速度v和全程的平均速度$\overline{v}$,二者有什么关系?
(2)试推导列车行驶至该段位移中点处的速度$v_{\frac{x}{2}}$
(3)请借助该v−t图像,找到位移中点和时间中点的速度,并比较它们的大小。
[探究活动]
2022年1月10日,京港高铁赣州至深圳段开通运营“满月”。一个月以来,该路段高铁为旅客提供了更为便捷、舒适的乘车体验,共计发送旅客22万人次。如图所示的为高铁列车从赣州车站出站后一段位移内的v−t图像。

(1)试通过v−t图像求出列车出站$\frac{t}{2}$时刻的速度v和全程的平均速度$\overline{v}$,二者有什么关系?
(2)试推导列车行驶至该段位移中点处的速度$v_{\frac{x}{2}}$
(3)请借助该v−t图像,找到位移中点和时间中点的速度,并比较它们的大小。
答案:
(1)$v - t$图线与t轴围成图形的面积等于位移的大小,则$x=\frac{v_{0}+v}{2}t$,可知列车在全程的平均速度$\overline{v}=\frac{x}{t}=\frac{v_{0}+v}{2}$,加速度$a=\frac{v - v_{0}}{t}$,可得到列车在出站$\frac{t}{2}$时刻的速度$v_{\frac{t}{2}}=v_{0}+a\cdot\frac{t}{2}=\frac{v_{0}+v}{2}$。可以看出中间时刻的速度等于全程的平均速度。
(2)$v_{\frac{x}{2}}=\sqrt{\frac{v_{0}^{2}+v^{2}}{2}}$。
(3)无论匀加速还是匀减速都是$v_{\frac{x}{2}}>v_{\frac{t}{2}}$。
(1)$v - t$图线与t轴围成图形的面积等于位移的大小,则$x=\frac{v_{0}+v}{2}t$,可知列车在全程的平均速度$\overline{v}=\frac{x}{t}=\frac{v_{0}+v}{2}$,加速度$a=\frac{v - v_{0}}{t}$,可得到列车在出站$\frac{t}{2}$时刻的速度$v_{\frac{t}{2}}=v_{0}+a\cdot\frac{t}{2}=\frac{v_{0}+v}{2}$。可以看出中间时刻的速度等于全程的平均速度。
(2)$v_{\frac{x}{2}}=\sqrt{\frac{v_{0}^{2}+v^{2}}{2}}$。
(3)无论匀加速还是匀减速都是$v_{\frac{x}{2}}>v_{\frac{t}{2}}$。
1.某做匀加速直线运动的物体初速度为2m/s,经过一段时间t后速度变为6m/s,则$\frac{t}{2}$时刻的速度为 ( )
A.由于t未知,无法确定$\frac{t}{2}$时刻的速度
B.由于加速度a及时间t未知,无法确定$\frac{t}{2}$时刻的速度
C.5m/s
D.4m/s
A.由于t未知,无法确定$\frac{t}{2}$时刻的速度
B.由于加速度a及时间t未知,无法确定$\frac{t}{2}$时刻的速度
C.5m/s
D.4m/s
答案:
D 解析:由匀变速直线运动在某段时间内中间时刻的瞬时速度等于这段时间内的平均速度可得,该物体在$\frac{t}{2}$时刻的速度为v = $\overline{v}$ = $\frac{v₀ + v}{2}$ = $\frac{2 + 6}{2}$m/s = 4m/s,故选D。
2.做匀加速直线运动的物体先后经过A、B两点的速度分别是和7,经历的时间为T,则下列各项中正确的是 ( )

A.经过A、B中点时的速度是4v
B.经过A、B中间时刻的速度是5v
C.前半程的速度增加了4v
D.前$\frac{T}{2}$时间的位移与后$\frac{t}{2}$时间的位移之比为1:3

A.经过A、B中点时的速度是4v
B.经过A、B中间时刻的速度是5v
C.前半程的速度增加了4v
D.前$\frac{T}{2}$时间的位移与后$\frac{t}{2}$时间的位移之比为1:3
答案:
C 解析:经过A、B中点的速度为v$_{\frac{s}{2}}$ = $\sqrt{\frac{v₀² + v²}{2}}$ = 5v,A错误;经过A、B中间时刻的速度为v$_{\frac{t}{2}}$ = $\frac{v₀ + v}{2}$ = 4v,B错误;由上可得v$_{\frac{s}{2}}$ = 5v,前半程的速度增加量为Δv = 5v - v = 4v,故C正确;由上可得v$_{\frac{s}{2}}$ = 5v,前$\frac{t}{2}$时间通过的位移为x₁ = \frac{v₀ + v_{\frac{t}{2}}}{2}\frac{t}{2}$ = $\frac{5}{4}$vt,后$\frac{t}{2}$时间通过的位移为x₂ = $\frac{v$_{\frac{t}{2}}$ + v}{2}\frac{t}{2}$ = $\frac{11}{4}$vt,可得,前$\frac{t}{2}$时间通过的位移与后$\frac{t}{2}$时间通过的位移之比为x₁:x₂ = 5:11,D错误。故选C。
3.二十大报告点赞“深海深地探测”。如图所示,2020年11月10日,奋斗者号成功坐底马里亚纳海沟,创下中国载人深潜10909m新纪录,奋斗者号完成作业后上浮,上浮过程初期可视为匀加速直线运动,现测得奋斗者号在上浮过程初期连续经过距离为8m的两段位移,第一段用时4s,第二段用时2s,则其加速度大小为 ( )

A.$\frac{16}{9}$m/s² B.$\frac{8}{9}$m/s²
C.$\frac{4}{3}$m/s² D.$\frac{2}{3}$m/s²

A.$\frac{16}{9}$m/s² B.$\frac{8}{9}$m/s²
C.$\frac{4}{3}$m/s² D.$\frac{2}{3}$m/s²
答案:
D 解析:第一个8m内的平均速度等于第一段中间时刻的瞬时速度,即v₁ = $\frac{x}{t}$ = $\frac{8}{4}$m/s = 2m/s,第二个8m内的平均速度等于第二段中间时刻的瞬时速度,即v₂ = $\frac{x}{t₂}$ = $\frac{8}{2}$m/s = 4m/s,第一段的中间时刻与第二段的中间时刻,时间间隔为t = $\frac{t}{2}$ + $\frac{t₂}{2}$ = 3s,根据速度时间关系有v₂ = v₁ + at,解得加速度为a = $\frac{v₂ - v₁}{t}$ = $\frac{4 - 2}{3}$m/s² = $\frac{2}{3}$m/s²,故选D。
第二章匀变速直线运动的研究任务四初速度为0的匀变速直线运动的比例关系
[探究活动]
对初速度为0的匀变速直线运动,设T 为时间单位,X为位移单位。
(1)1T末、2T末、3T末……瞬时速度之比:
由v=at,得v1:v2:v3:…….:vn=____
。
(2)1T内、2T内、3T内……位移之比:
由x=$\frac{1}{2}$at²,得x1:x2:x3:.….:xn=
________________________。
(3)第一个T内、第二个T内、第三个T 内……位移之比:
由xI=x1、xII=x2−x1……可得xI:xII:xIII:...:xN=____________________。
(4)通过1X、2X、3X……所用时间之比:由x=$\frac{1}{2}$at2知t=$\sqrt{\frac{2x}{a}}$,可得t1:t2:t3:...:tn=________________。
(5)通过第一个X、第二个X、第三个X……所用时间之比:
由tI=t1、tII=t2−t1……可得tI:tII:tIII:...:tN=__________________________。
[探究活动]
对初速度为0的匀变速直线运动,设T 为时间单位,X为位移单位。
(1)1T末、2T末、3T末……瞬时速度之比:
由v=at,得v1:v2:v3:…….:vn=____
。
(2)1T内、2T内、3T内……位移之比:
由x=$\frac{1}{2}$at²,得x1:x2:x3:.….:xn=
________________________。
(3)第一个T内、第二个T内、第三个T 内……位移之比:
由xI=x1、xII=x2−x1……可得xI:xII:xIII:...:xN=____________________。
(4)通过1X、2X、3X……所用时间之比:由x=$\frac{1}{2}$at2知t=$\sqrt{\frac{2x}{a}}$,可得t1:t2:t3:...:tn=________________。
(5)通过第一个X、第二个X、第三个X……所用时间之比:
由tI=t1、tII=t2−t1……可得tI:tII:tIII:...:tN=__________________________。
答案:
(1)1:2:3:……:n
(2)1²:2²:3²:……:n²
(3)1:3:5:……:(2n - 1)
(4)1:$\sqrt{2}$:$\sqrt{3}$:……:$\sqrt{n}$
(5)1:($\sqrt{2}$ - 1):($\sqrt{3}$ - $\sqrt{2}$):……:($\sqrt{n}$ - $\sqrt{n - 1}$)
(1)1:2:3:……:n
(2)1²:2²:3²:……:n²
(3)1:3:5:……:(2n - 1)
(4)1:$\sqrt{2}$:$\sqrt{3}$:……:$\sqrt{n}$
(5)1:($\sqrt{2}$ - 1):($\sqrt{3}$ - $\sqrt{2}$):……:($\sqrt{n}$ - $\sqrt{n - 1}$)
1.一个物体从静止开始做匀加速直线运动,它在第1s内与第2s内的位移之比为x1:x2,在走完第1m时与走完前2m时的速度之比为v1:v2。以下说法正确的是( )
A.x1:x2=1:3,v1:v2=1:2
B.x1:x2=1:3,v1:v2=1:$\sqrt{2}$
C.x1:x2=1:4,v1:v2=1:2
D.x1:x2=1:4,v1:v2=1:$\sqrt{2}$
A.x1:x2=1:3,v1:v2=1:2
B.x1:x2=1:3,v1:v2=1:$\sqrt{2}$
C.x1:x2=1:4,v1:v2=1:2
D.x1:x2=1:4,v1:v2=1:$\sqrt{2}$
答案:
B 解析:由匀变速直线运动连续相等时间内的位移之比x₁:x₂:x₃:……:xₙ = 1:3:5:……:(2n - 1)知x₁:x₂ = 1:3。由x = $\frac{1}{2}$at²知走完第1m和前2m的时间之比为t₁:t₂ = 1:$\sqrt{2}$,又由v = at可得v₁:v₂ = 1:$\sqrt{2}$,选项B正确。
2.(多选)如图所示,水平地面上有固定两块木板AB、BC,紧挨在一起,木板AB的长度是BC的3倍,一颗子弹以初速度v。从A端射入木板,并恰能从C端射出,用的时间为t,子弹在木板中的运动可以看成是匀变速运动,则以下说法正确的是 ( )

A.子弹到B点的速度为$\frac{Vo}{4}$
B.子弹到B点的速度为$\frac{Vo}{2}$
C.子弹从A到B的时间为$\frac{t}{4}$
D.子弹从A到B的时间为$\frac{t}{2}$

A.子弹到B点的速度为$\frac{Vo}{4}$
B.子弹到B点的速度为$\frac{Vo}{2}$
C.子弹从A到B的时间为$\frac{t}{4}$
D.子弹从A到B的时间为$\frac{t}{2}$
答案:
BD 解析:初速度为0的匀加速直线运动,相同时间的位移比为1:3,可以把子弹的运动反向看成初速度为0的匀加速直线运动,由于木板AB的长度是BC的3倍,故子弹经过AB和BC的时间相等,均为$\frac{t}{2}$,故C错误,D正确;初速度为0的匀加速直线运动,经过连续的相同时间间隔的速度比为1:2,由于子弹以初速度v₀从A端射入木板,可知子弹到B的速度为$\frac{v₀}{2}$,A错误,B正确。
3.(多选)如图所示的是珠港澳大桥上四段110m的等跨钢箱连续梁桥,桥墩标记为a、b、c、d、e,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则汽车( )
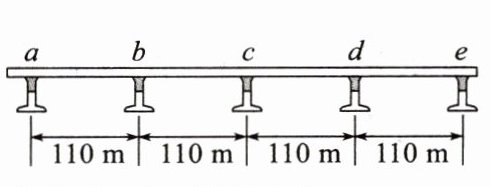
A.通过bc段的时间也为t
B.通过ae段的时间为2t
C.汽车通过b、c、d、e的速度之比为1:2:3:4
D.汽车通过b、c、d、e的速度之比为1:$\sqrt{2}$:$\sqrt{3}$:2

A.通过bc段的时间也为t
B.通过ae段的时间为2t
C.汽车通过b、c、d、e的速度之比为1:2:3:4
D.汽车通过b、c、d、e的速度之比为1:$\sqrt{2}$:$\sqrt{3}$:2
答案:
BD 解析:根据初速度为0的匀加速直线运动的规律可知,通过连续相等位移所用的时间之比为1:($\sqrt{2}$ - 1):($\sqrt{3}$ - $\sqrt{2}$):……:($\sqrt{n}$ - $\sqrt{n - 1}$),通过ab段的时间为t,可得出通过bc时间为($\sqrt{2}$ - 1)t,通过ae段的时间为t$_{ae}$ = t + ($\sqrt{2}$ - 1)t + ($\sqrt{3}$ - $\sqrt{2}$)t + (2 - $\sqrt{3}$)t = 2t,故A错误,B正确;通过连续相等位移的末速度之比为1:$\sqrt{2}$:$\sqrt{3}$:……:$\sqrt{n}$,则汽车通过b、c、d、e的速度之比为1:$\sqrt{2}$:$\sqrt{3}$:2,故C错误,D正确。
4.一列复兴号动车进站时做匀减速直线运动,车头依次从站台上三个立柱A、B、C旁经过,相邻两立柱间的距离均为α。,对应时刻分别为t1、t2、t3。下列说法正确的是
( )
A.车头经过立柱B时的速度为$\frac{2x。}{t3−t}$
B.车头在立柱A、B之间的平均速度等于$\frac{xo}{t2−t}$
C.三个时刻间的关系为(t3−t2):(t2一t1)=1:( $\sqrt{2}$−1)
D.车头经过A、B、C时的速度vA、vB、vc大小关系为2vB=vA+vc
( )
A.车头经过立柱B时的速度为$\frac{2x。}{t3−t}$
B.车头在立柱A、B之间的平均速度等于$\frac{xo}{t2−t}$
C.三个时刻间的关系为(t3−t2):(t2一t1)=1:( $\sqrt{2}$−1)
D.车头经过A、B、C时的速度vA、vB、vc大小关系为2vB=vA+vc
答案:
B 解析:车头从立柱A到立柱C的平均速度$\overline{v}_{AC}$ = $\frac{2x₀}{t₃ - t₁}$,立柱B位于A、C的中点,根据匀变速直线运动的推论可知,一段时间内位移中点的瞬时速度大于中间时刻的瞬时速度,而中间时刻的瞬时速度等于这段时间内的平均速度,故车头经过B立柱时的瞬时速度大于$\frac{2x₀}{t₃ - t₁}$,故A错误;车头在立柱A、B之间的平均速度为$\overline{v}_{AB}$ = $\frac{x₀}{t₂ - t₁}$,故B正确;若t₃时刻速度减为0,则根据逆向思维结合相等位移的时间关系可知(t₃ - t₂):(t₂ - t₁) = 1:($\sqrt{2}$ - 1),因t₃时刻速度不一定减为0,则选项C错误;因B立柱对应的不是A、C的中间时刻,故不满足v$_{B}$ = $\frac{v_{A} + v_{C}}{2}$,选项D错误。
1. 认真观察教材中的“轻重不同的物体下落快慢的研究”演示实验,有空气时,铁片明显比羽毛下落得快,没有空气时,它们下落一样快。那么由羽毛和铁片的运动所遵循的规律可以得出怎样的结论?
答案:
提示:如果没有空气阻力,羽毛和铁片下落的快慢一样,遵循相同的运动规律。
2. 根据预习我们知道,自由落体运动的本质是初速度________的____________运动,它们的受力特点是________。
答案:
为0 匀加速直线 只受重力
[微训练]
1. 在空气中自由释放的物体做自由落体运动。( )
2. 物体在真空中一定做自由落体运动。( )
3. 只在重力作用下自由释放的物体一定做自由落体运动。( )
1. 在空气中自由释放的物体做自由落体运动。( )
2. 物体在真空中一定做自由落体运动。( )
3. 只在重力作用下自由释放的物体一定做自由落体运动。( )
答案:
×
@@×
@@√
@@×
@@√
2. 自由落体加速度
(1) 在同一地点,一切物体自由下落的加速度都________,这个加速度叫作自由落体加速度,也叫作____________,通常用g表示。
(2) 方向:____________。
(3) 大小:在地球表面不同的地方,g的大小一般是________。计算中g一般取9.8m/s²或10m/s²。
(1) 在同一地点,一切物体自由下落的加速度都________,这个加速度叫作自由落体加速度,也叫作____________,通常用g表示。
(2) 方向:____________。
(3) 大小:在地球表面不同的地方,g的大小一般是________。计算中g一般取9.8m/s²或10m/s²。
答案:
(1)相同 重力加速度
(2)竖直向下
(3)不同的
(1)相同 重力加速度
(2)竖直向下
(3)不同的
3. 自由落体运动的基本公式
速度公式:v = ________。
位移公式:h = ________。
位移与速度关系式:v² = ________。
速度公式:v = ________。
位移公式:h = ________。
位移与速度关系式:v² = ________。
答案:
gt $\frac{1}{2}$gt² $\sqrt{2gh}$
[微训练]
1. 物体越重,重力加速度越大,下落得越快。( )
2. 自由落体运动的速度大小与时间成正比。( )
3. 自由落体运动的位移大小与时间成正比。( )
4. 自由落体运动的速度的平方与位移成正比。( )
1. 物体越重,重力加速度越大,下落得越快。( )
2. 自由落体运动的速度大小与时间成正比。( )
3. 自由落体运动的位移大小与时间成正比。( )
4. 自由落体运动的速度的平方与位移成正比。( )
答案:
×
@@√
@@×
@@√
@@√
@@×
@@√
1. (多选)关于自由落体运动,下列说法正确的是( )
A. 竖直向下的运动一定是自由落体运动
B. 自由落体运动是初速度为0、加速度为g 的竖直向下的匀加速直线运动
C. 物体只在重力作用下从静止开始下落的运动叫自由落体运动
D. 熟透的苹果从树枝脱落并开始自由下落的运动可被视为自由落体运动
A. 竖直向下的运动一定是自由落体运动
B. 自由落体运动是初速度为0、加速度为g 的竖直向下的匀加速直线运动
C. 物体只在重力作用下从静止开始下落的运动叫自由落体运动
D. 熟透的苹果从树枝脱落并开始自由下落的运动可被视为自由落体运动
答案:
BCD 解析:物体做自由落体运动的条件是初速度为0且只受重力作用,故A错误,C正确;所有物体做自由落体运动的加速度均为g,运动性质均是由静止开始的匀加速直线运动,故B 正确;熟透的苹果在下落过程中虽受空气阻力作用,但该阻力远小于它的重力,可以忽略该阻力的影响,则可将该过程视为自由落体运动,故D 正确。
2. 踢毽子是我国民间的一项体育游戏,被人们誉为“生命的蝴蝶”,如图所示。近年来,踢毽子成为全民健身活动之一。毽子由羽毛和铜钱组成,在下落时总是铜钱在下羽毛在上。对此分析正确的是( )

A. 铜钱重,所以总是铜钱在下羽毛在上
B. 如果没有空气阻力,也总是出现铜钱在下羽毛在上的现象
C. 因为空气阻力的存在,所以总是铜钱在下羽毛在上
D. 毽子的下落是自由落体运动

A. 铜钱重,所以总是铜钱在下羽毛在上
B. 如果没有空气阻力,也总是出现铜钱在下羽毛在上的现象
C. 因为空气阻力的存在,所以总是铜钱在下羽毛在上
D. 毽子的下落是自由落体运动
答案:
C 解析:羽毛受到的空气阻力与自身重力相差不多,对运动的影响很大,而羽毛又和铜钱连接在一起,故羽毛要受铜钱较大的拖动作用,即羽毛的运动主要是靠铜钱的带动,所以毽子下落时总是铜钱在下面拉着羽毛,铜钱重不是根本原因,A错误,C正确;如果没有空气阻力,铜钱和羽毛的相对位置是随机的,B错误;由以上分析可知,毽子受到的空气阻力不能忽略,毽子的下落不是自由落体运动,D错误。
3. 如图所示的为玉兔号在没有空气的月球上工作的场景。若在航天飞行控制中心的精确控制下,玉兔号使用机械臂从月壤中采集两个质量不同的石块,然后从同一高度同时由静止释放,下列判断正确的是( )

A. 质量大的石块先落到月球上
B. 质量小的石块先落到月球上
C. 质量大的石块落到月球上时的速度大
D. 两个石块落到月球上时的速度一样大

A. 质量大的石块先落到月球上
B. 质量小的石块先落到月球上
C. 质量大的石块落到月球上时的速度大
D. 两个石块落到月球上时的速度一样大
答案:
D 解析:两个石块都做自由落体运动,它们的运动的情况是完全相同的,所以它们的加速度相同,落到地面所用时间相同,落地速度相同,A、B、C错误,D正确。
1. 某同学利用物体的自由落体运动测量重力加速度,实验装置如图甲所示,打点计时器接在频率为50Hz的交流电源上。使重锤自由下落,打点计时器在随重锤下落的纸带上打下一系列点迹。挑出点迹清晰的一条纸带,依次标出计数点1, 2, …, 8,相邻计数点之间还有1个计时点。分别测出相邻计数点之间的距离x1, x2, …, x7,并求出计数点2, 3, …, 7对应的重锤速度。在坐标纸上建立v - t坐标系,根据重锤下落的速度作出v - t图像并求重力加速度。

(1) 图乙为纸带的一部分,打点3时,重锤下落的速度v3 = ________m/s(结果保留三位有效数字)。

(2) 除点3外,其余各计数点的速度对应的坐标点已在图丙所示的坐标系中标出,请在图中标出速度v3对应的坐标点,并作出v - t图像。

(3) 根据图丙,实验测得的重力加速度g = ________m/s²(结果保留三位有效数字)。
(4) 某同学居家学习期间,注意到一水龙头距地面较高,而且发现通过调节水龙头阀门可实现水滴逐滴下落,并能控制相邻水滴开始下落的时间间隔,还能听到水滴落地时发出的清脆声音。于是他计划利用手机的秒表计时功能和刻度尺测量重力加速度。为准确测量,请写出需要测量的物理量及对应的测量方法。

(1) 图乙为纸带的一部分,打点3时,重锤下落的速度v3 = ________m/s(结果保留三位有效数字)。

(2) 除点3外,其余各计数点的速度对应的坐标点已在图丙所示的坐标系中标出,请在图中标出速度v3对应的坐标点,并作出v - t图像。

(3) 根据图丙,实验测得的重力加速度g = ________m/s²(结果保留三位有效数字)。
(4) 某同学居家学习期间,注意到一水龙头距地面较高,而且发现通过调节水龙头阀门可实现水滴逐滴下落,并能控制相邻水滴开始下落的时间间隔,还能听到水滴落地时发出的清脆声音。于是他计划利用手机的秒表计时功能和刻度尺测量重力加速度。为准确测量,请写出需要测量的物理量及对应的测量方法。
答案:
解析:
(1)打点计时器接在频率为50.0Hz的交流电源上,相邻计数点之间还有1个计时点,则相邻两计数点之间的时间间隔为t = 2×0.02s = 0.04s。纸带做自由落体运动,打点3时的瞬时速度等于点2到点4之间的平均速度,由纸带数据可知$v_3 = \frac{x_{24}}{2t} = 1.15m/s$。
(2)如图所示。

(3)根据$v = gt$,可知$g = \frac{v}{t}$,根据$v - t$图像可知其斜率为重力加速度,则有$g = \frac{2.7 - 0.35}{0.24}m/s²≈9.79m/s²$。
(4)需要测量的物理量有水滴下落的高度h和下落的时间t。测量h的方法:用刻度尺测量水龙头出水口到地面的高度,多次测量取平均值;测量t的方法:调节水龙头阀门,使一滴水开始下落的同时,恰好听到前一滴水落地时发出的清脆声音。用手机测量n滴水下落的总时间$t_n$,则$t = \frac{t_n}{n}$。
答案:
(1)1.15
(2)见解析图
(3)9.79
(4)见解析
解析:
(1)打点计时器接在频率为50.0Hz的交流电源上,相邻计数点之间还有1个计时点,则相邻两计数点之间的时间间隔为t = 2×0.02s = 0.04s。纸带做自由落体运动,打点3时的瞬时速度等于点2到点4之间的平均速度,由纸带数据可知$v_3 = \frac{x_{24}}{2t} = 1.15m/s$。
(2)如图所示。

(3)根据$v = gt$,可知$g = \frac{v}{t}$,根据$v - t$图像可知其斜率为重力加速度,则有$g = \frac{2.7 - 0.35}{0.24}m/s²≈9.79m/s²$。
(4)需要测量的物理量有水滴下落的高度h和下落的时间t。测量h的方法:用刻度尺测量水龙头出水口到地面的高度,多次测量取平均值;测量t的方法:调节水龙头阀门,使一滴水开始下落的同时,恰好听到前一滴水落地时发出的清脆声音。用手机测量n滴水下落的总时间$t_n$,则$t = \frac{t_n}{n}$。
答案:
(1)1.15
(2)见解析图
(3)9.79
(4)见解析
2. 光电门是一个像门一样的装置,一边安装激光发射端a,一边安装接收端b,并与计时装置连接,如图甲所示,细激光束从a射向b,当有物体通过光电门挡住细激光束时,光电计时器可以记录下挡光时间。某同学利用如图乙所示的装置测量当地的重力加速度:在铁架台顶部装一电磁铁,中间装一可上下移动的光电门,光电门a、b间的细激光束处于水平状态,左侧装一竖直刻度尺。用电磁铁吸住一个质量为m的小球,调节电磁铁的位置,使小钢球由静止释放后球心恰好能通过激光束。记录光电门的细激光束与释放前小钢球球心间的距离x。

(1) 若小钢球的直径为d(d比x小很多),则小钢球通过光电门过程中的平均速度为________。
(2) 当地的重力加速度大小为________(用d、t、x表示)。
(3) 实验中,若测得的重力加速度值比实际真实值大,可能的原因是________。
A. 电磁铁断电后仍有磁性
B. 球心没有在细激光束正上方,导致操作时小钢球的球心并没有通过细激光束
C. 光电门轴线ab不是处于水平状态
D. 小钢球所受空气阻力偏大

(1) 若小钢球的直径为d(d比x小很多),则小钢球通过光电门过程中的平均速度为________。
(2) 当地的重力加速度大小为________(用d、t、x表示)。
(3) 实验中,若测得的重力加速度值比实际真实值大,可能的原因是________。
A. 电磁铁断电后仍有磁性
B. 球心没有在细激光束正上方,导致操作时小钢球的球心并没有通过细激光束
C. 光电门轴线ab不是处于水平状态
D. 小钢球所受空气阻力偏大
答案:
解析:
(1)小钢球通过光电门的平均速度为$v = \frac{d}{t}$。
(2)小钢球做自由落体运动,因小钢球经过光电门的时间很小,其平均速度近似等于瞬时速度,由速度与位移关系式可得$v² = (\frac{d}{t})² = 2gx$,解得$g = \frac{d²}{2xt²}$。
(3)若电磁铁断电后仍有磁性,小钢球在下落时会受到一个向上的力的作用,下落时速度变化缓慢,则经过光电门的时间t变大,使得重力加速度的测量值比实际真实值小,A错误;球心没有在细激光束正上方时,导致操作时小钢球的球心并没有通过细激光束,挡住细激光束的距离小于d,导致小钢球经过光电门的时间t减小,但计算时仍按d计算,使得测得的重力加速度比实际真实值大,B正确;若光电门轴线ab 不是处于水平状态,小钢球经过光电门时的挡光距离增大,即时间t变大,计算时仍按d计算,使得重力加速度的测量值比实际真实值小,C错误;若小钢球所受空气阻力偏大,小钢球下落时速度减小,经过光电门的时间t变大,则重力加速度的测量值比实际真实值小,D错误。
答案:
(1)$\frac{d}{t}$
(2)$\frac{d²}{2xt²}$
(3)B
(1)小钢球通过光电门的平均速度为$v = \frac{d}{t}$。
(2)小钢球做自由落体运动,因小钢球经过光电门的时间很小,其平均速度近似等于瞬时速度,由速度与位移关系式可得$v² = (\frac{d}{t})² = 2gx$,解得$g = \frac{d²}{2xt²}$。
(3)若电磁铁断电后仍有磁性,小钢球在下落时会受到一个向上的力的作用,下落时速度变化缓慢,则经过光电门的时间t变大,使得重力加速度的测量值比实际真实值小,A错误;球心没有在细激光束正上方时,导致操作时小钢球的球心并没有通过细激光束,挡住细激光束的距离小于d,导致小钢球经过光电门的时间t减小,但计算时仍按d计算,使得测得的重力加速度比实际真实值大,B正确;若光电门轴线ab 不是处于水平状态,小钢球经过光电门时的挡光距离增大,即时间t变大,计算时仍按d计算,使得重力加速度的测量值比实际真实值小,C错误;若小钢球所受空气阻力偏大,小钢球下落时速度减小,经过光电门的时间t变大,则重力加速度的测量值比实际真实值小,D错误。
答案:
(1)$\frac{d}{t}$
(2)$\frac{d²}{2xt²}$
(3)B
3. 小明同学在家自主开展实验探究,他用手机拍摄物体自由下落的视频,得到分帧图片,利用图片中小球的位置来测量当地的重力加速度,实验装置如图甲所示。
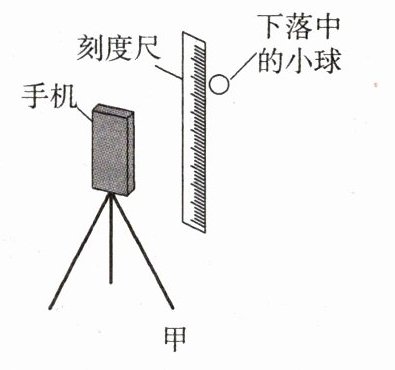
(1) 家中有乒乓球、小塑料球和小钢球,其中最适合用作实验中下落物体的是________。
(2) 下列主要操作步骤的正确顺序是______(填写各步骤前的序号)。
① 把刻度尺竖直固定在墙上;
② 捏住小球,从刻度尺旁由静止释放;
③ 手机固定在三脚架上,调整好手机镜头的位置;
④ 打开手机摄像功能,开始摄像。
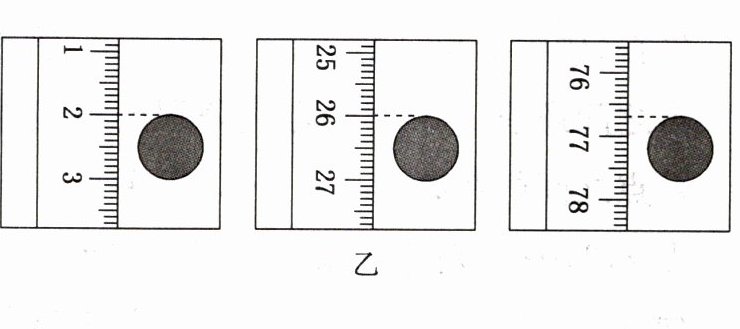
(3) 停止摄像后,从视频中截取三帧图片,图片中小球的位置如图乙所示。已知所截取的图片相邻两帧之间的时间间隔为$\frac{1}{6}$s,刻度尺的分度值是1mm,由此测得重力加速度为______m/s²(结果保留两位有效数字)。

(1) 家中有乒乓球、小塑料球和小钢球,其中最适合用作实验中下落物体的是________。
(2) 下列主要操作步骤的正确顺序是______(填写各步骤前的序号)。
① 把刻度尺竖直固定在墙上;
② 捏住小球,从刻度尺旁由静止释放;
③ 手机固定在三脚架上,调整好手机镜头的位置;
④ 打开手机摄像功能,开始摄像。
(3) 停止摄像后,从视频中截取三帧图片,图片中小球的位置如图乙所示。已知所截取的图片相邻两帧之间的时间间隔为$\frac{1}{6}$s,刻度尺的分度值是1mm,由此测得重力加速度为______m/s²(结果保留两位有效数字)。

答案:
解析:
(1)与乒乓球、小塑料球相比,小钢球受到的空气阻力远小于其重力,可忽略不计,故小钢球的运动可看作自由落体运动。
(2)根据实验操作要求,应先固定刻度尺,然后固定手机,调整好手机镜头的位置,打开手机摄像功能进行摄像,最后捏住小球,使小球从刻度尺旁由静止下落,即步骤的正确顺序为①③④②。
(3)题图乙左侧图片中小球上边缘的读数为2.00cm,中间图片中小球上边缘的读数为26.00cm,右侧图片中小球上边缘的读数为76.70cm,由逐差法可得当地的重力加速度大小为$g = 9.6m/s²$。
答案:
(1)小钢球
(2)①③④②
(3)9.6
(1)与乒乓球、小塑料球相比,小钢球受到的空气阻力远小于其重力,可忽略不计,故小钢球的运动可看作自由落体运动。
(2)根据实验操作要求,应先固定刻度尺,然后固定手机,调整好手机镜头的位置,打开手机摄像功能进行摄像,最后捏住小球,使小球从刻度尺旁由静止下落,即步骤的正确顺序为①③④②。
(3)题图乙左侧图片中小球上边缘的读数为2.00cm,中间图片中小球上边缘的读数为26.00cm,右侧图片中小球上边缘的读数为76.70cm,由逐差法可得当地的重力加速度大小为$g = 9.6m/s²$。
答案:
(1)小钢球
(2)①③④②
(3)9.6
1. 科技馆中有一个展品,如图所示。在较暗处有一个不断均匀滴水的水龙头,在一种特殊的灯光照射下,可观察到一个个下落的水滴。缓缓调节水滴下落的时间间隔到适当情况,可看到一种奇特的现象,水滴似乎不再往下落,而是固定在图中A、B、C、D四个位置不动,要出现这种现象,照明光源应该满足(取g = 10m/s²)( )
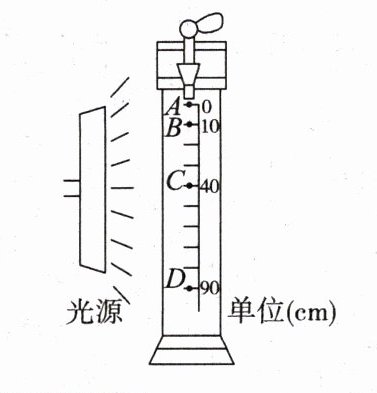
A. 普通光源即可
B. 间歇发光,间隙时间为0.14s
C. 间歇发光,间隙时间为2.4s
D. 间歇发光,间隙时间为0.2s

A. 普通光源即可
B. 间歇发光,间隙时间为0.14s
C. 间歇发光,间隙时间为2.4s
D. 间歇发光,间隙时间为0.2s
答案:
B 解析:由题意可知,光源需间歇发光,间隙时间等于相邻两滴水的时间间隔的整数倍,相邻两段位移差的平均值为20cm,根据$\Delta y = gT²$,解得$T = 0.14s$,故选B。
2. (多选)《民法典》第一千二百五十四条规定:禁止从建筑物中抛掷物品。从建筑物中抛掷物品或者从建筑物上坠落的物品造成他人损害的,由侵权人依法承担侵权责任。某中学物理实验小组做了一个相关实验,在20m高的阳台上由静止释放一颗小石子,不计空气阻力,g = 10m/s²,则下列说法正确的是( )
A. 下落时间为2s
B. 落地速度为20m/s
C. 下落过程的速度变化量为10m/s
D. 下落过程的速度变化率为5m/s²
A. 下落时间为2s
B. 落地速度为20m/s
C. 下落过程的速度变化量为10m/s
D. 下落过程的速度变化率为5m/s²
答案:
AB 解析:根据$h = \frac{1}{2}gt²$,得下落时间为$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2×20}{10}}s = 2s$,故A正确;落地速度为$v = gt = 20m/s$,故B正确;下落过程的速度变化量为$\Delta v = 20m/s$,故C错误;下落过程的加速度为$g = 10m/s²$,速度变化率为$10m/s²$,故D 错误。
3. 如图所示,某同学测出一棵苹果树树干部分的高度约为1.6m,一个苹果由于受到扰动而从树冠顶端的树梢上自由下落,该同学测出苹果经过树干所用的时间为0.2s,取g = 10m/s²,则:
(1) 苹果树树冠部分的高度约为多少?
(2) 苹果落地时的速度为多大?
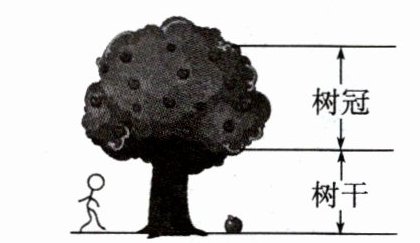
(1) 苹果树树冠部分的高度约为多少?
(2) 苹果落地时的速度为多大?

答案:
解析:
(1)设苹果树树冠部分的高度为$h_1$,则有$h_1 = \frac{1}{2}gt_1²$,$h_1 + 1.6m = \frac{1}{2}g(t_1 + 0.2s)²$。
解得$t_1 = 0.7s$,$h_1 = 2.45m$。
(2)苹果落地时的速度为$v = gt = g(t_1 + 0.2s) = 9m/s$。
答案:
(1)2.45m
(2)9m/s
(1)设苹果树树冠部分的高度为$h_1$,则有$h_1 = \frac{1}{2}gt_1²$,$h_1 + 1.6m = \frac{1}{2}g(t_1 + 0.2s)²$。
解得$t_1 = 0.7s$,$h_1 = 2.45m$。
(2)苹果落地时的速度为$v = gt = g(t_1 + 0.2s) = 9m/s$。
答案:
(1)2.45m
(2)9m/s
1. (多选)如图所示,在一个桌面上方有三个金属小球a、b、c,离桌面的高度分别为h1:h2:h3 = 3:2:1。若先后释放a、b、c,三球刚好同时落到桌面上,不计空气阻力,则( )
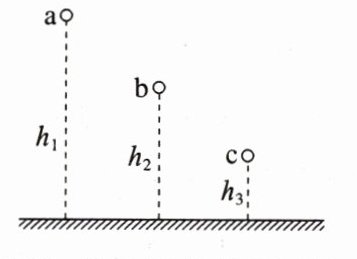
A. 三者到达桌面时的速度大小之比是$\sqrt{3}$:$\sqrt{2}$:1
B. 三者运动时间之比为3:2:1
C. b与a开始下落的时间差小于c与b开始下落的时间差
D. 三个小球运动的加速度与小球受到的重力成正比

A. 三者到达桌面时的速度大小之比是$\sqrt{3}$:$\sqrt{2}$:1
B. 三者运动时间之比为3:2:1
C. b与a开始下落的时间差小于c与b开始下落的时间差
D. 三个小球运动的加速度与小球受到的重力成正比
答案:
1.AC 解析:设$h_3 = h$,则由$v² = 2gh$,得$v = \sqrt{2gh}$,则到达桌面时的速度大小之比$v_1:v_2:v_3 = \sqrt{3h}:\sqrt{2h}:\sqrt{h} = \sqrt{3}:\sqrt{2}:1$,故A正确;由$h = \frac{1}{2}gt²$,则$t = \sqrt{\frac{2h}{g}}$,得三者的运动时间之比$t_1:t_2:t_3 = \sqrt{3}:\sqrt{2}:1$,故B错误;b与a开始下落的时间差$\Delta t_1 = (\sqrt{3} - \sqrt{2})\sqrt{\frac{2h_3}{g}}$,c与b 开始下落的时间差$\Delta t_2 = (\sqrt{2} - 1)\sqrt{\frac{2h_3}{g}}$,即b 与a开始下落的时间差小于c与b开始下落的时间差,故C正确;三个小球的加速度与重力和质量无关,均等于重力加速度,故D错误。
2. 热气球运动爱好者从某高处由静止释放一个质量为0.5kg的物体,地面测量人员测量发现物体在落地前1s内下落的高度是40m,不考虑空气阻力,取g = 10m/s²。下列说法正确的是( )
A. 物体从释放到落地经历的时间为4.5s
B. 物体落地时的速度为40m/s
C. 从释放到落地物体运动的平均速度大小为20m/s
D. 物体下落的高度为80m
A. 物体从释放到落地经历的时间为4.5s
B. 物体落地时的速度为40m/s
C. 从释放到落地物体运动的平均速度大小为20m/s
D. 物体下落的高度为80m
答案:
2.A 解析:设物体下落时间为t,由题意可知物体落地前1s内的平均速度为40m/s,即为最后1s内中间时刻的速度,根据自由落体运动的规律有$40m/s = g(t - 0.5s)$,代入数据解得$t = 4.5s$,A正确;落地速度为$v = gt = 45m/s$,B错误。从释放到落地物体运动的平均速度为$\overline{v} = \frac{v}{2} = 22.5m/s$,C错误;物体下落的高度为$h = \frac{1}{2}gt² = 101.25m$,D错误。
3. (多选)如图所示,一长为L = 0.05m的铁链用短绳悬挂在天花板上,铁链正下方h = 0.2m处竖直放置一长度也为h、内径比铁链直径稍大的钢管。剪断轻绳,铁链由静止开始下落,不计空气阻力,取g = 10m/s²,则( )

A. 铁链上端刚要进入钢管时的速度大小为$\sqrt{5}$m/s
B. 铁链下端刚要穿出钢管时的速度大小为2$\sqrt{2}$m/s
C. 铁链通过钢管的时间为0.3s
D. 铁链通过钢管的时间为0.1s

A. 铁链上端刚要进入钢管时的速度大小为$\sqrt{5}$m/s
B. 铁链下端刚要穿出钢管时的速度大小为2$\sqrt{2}$m/s
C. 铁链通过钢管的时间为0.3s
D. 铁链通过钢管的时间为0.1s
答案:
3.ABD 解析:根据速度与位移关系式$v² = 2gh$,可得铁链上端刚要进入钢管时的速度大小为$v_1 = \sqrt{2gh} = \sqrt{5}m/s$,故A正确;铁链下端刚要穿出钢管时的速度大小为$v_2 = \sqrt{2gh_2} = 2\sqrt{2}m/s$,故B正确;根据$h = \frac{1}{2}gt²$,可得铁链下端刚要进入钢管时运动的时间$t_1 = 0.2s$,铁链上端刚要穿出钢管的运动时间为$t_2 = \sqrt{\frac{2(l + h + h_2)}{g}} = 0.3s$,铁链通过钢管的时间为$\Delta t = t_2 - t_1 = 0.1s$,故C错误,D正确。
4. 如图所示,一滴雨滴从离地面20m高的楼房屋檐自由下落,下落途中用△t = 0.2s的时间通过一个窗口,窗口的高度为2m,取g = 10m/s²,求:
(1) 雨滴落地时的速度大小;
(2) 雨滴落地前最后1s内的位移大小;
(3) 屋檐离窗的上边框有多高?

(1) 雨滴落地时的速度大小;
(2) 雨滴落地前最后1s内的位移大小;
(3) 屋檐离窗的上边框有多高?

答案:
4.解析:
(1)由$h = \frac{gt²}{2}$,得$t = 2s$,雨滴落地时的速度$v = gt = 20m/s$。
(2)雨滴在第1s内的位移$h_1 = \frac{gt_1²}{2} = 5m$,雨滴落地前最后1s内的位移$h_2 = h - h_1 = 15m$。
(3)设屋檐到窗的上边框的距离为$x_0$,雨滴从屋檐运动到窗的上边框所用的时间为$t_0$,则$x_0 = \frac{gt_0²}{2}$,$x_0 + 2m = \frac{g(t_0 + \Delta t)²}{2}$。
联立得$x_0 = 4.05m$。
答案:
(1)20m/s
(2)15m
(3)4.05m
(1)由$h = \frac{gt²}{2}$,得$t = 2s$,雨滴落地时的速度$v = gt = 20m/s$。
(2)雨滴在第1s内的位移$h_1 = \frac{gt_1²}{2} = 5m$,雨滴落地前最后1s内的位移$h_2 = h - h_1 = 15m$。
(3)设屋檐到窗的上边框的距离为$x_0$,雨滴从屋檐运动到窗的上边框所用的时间为$t_0$,则$x_0 = \frac{gt_0²}{2}$,$x_0 + 2m = \frac{g(t_0 + \Delta t)²}{2}$。
联立得$x_0 = 4.05m$。
答案:
(1)20m/s
(2)15m
(3)4.05m
#### 任务一 匀变速直线运动的基本规律和多过程运动的分析
活动:如图所示,某高楼距地面高H = 82m ,第二章匀变速直线运动的研究高空坠物及利用运动规律解决汽车安全行驶等问题的阳台上的花盆因受扰动而掉落,掉落过程可看作自由落体运动(花盆可视为质点)。

(1)若阳台下方停有一辆高h = 2m的汽车,试求花盆落到车顶时的速度大小。
(2)现有一辆长为L1 = 8m、高为h = 2m的货车,正以v0 = 10m/s的速度驶向阳台正下方的通道。花盆刚开始掉落时,货车车头距花盆的水平距离为L2 = 38m,由于道路限制,汽车只能直行通过阳台正下方的通道,取g = 10m/s²。若司机发现花盆开始掉落,司机反应时间△t = 2s,则司机采取什么方式可以避险?(货车加速、减速均可视为匀变速运动)
活动:如图所示,某高楼距地面高H = 82m ,第二章匀变速直线运动的研究高空坠物及利用运动规律解决汽车安全行驶等问题的阳台上的花盆因受扰动而掉落,掉落过程可看作自由落体运动(花盆可视为质点)。

(1)若阳台下方停有一辆高h = 2m的汽车,试求花盆落到车顶时的速度大小。
(2)现有一辆长为L1 = 8m、高为h = 2m的货车,正以v0 = 10m/s的速度驶向阳台正下方的通道。花盆刚开始掉落时,货车车头距花盆的水平距离为L2 = 38m,由于道路限制,汽车只能直行通过阳台正下方的通道,取g = 10m/s²。若司机发现花盆开始掉落,司机反应时间△t = 2s,则司机采取什么方式可以避险?(货车加速、减速均可视为匀变速运动)
答案:
提示:
(1)花盆从82m的高处落下,到达离地高2m的车顶,根据位移公式有
h = $\frac{1}{2}$gt² = (82 - 2)m = 80m,
代入数据解得t = 4s。
花盆落到车顶时的速度大小为v = gt = 40m/s。
(2)货车司机反应时间内通过的距离为
Δx = v₀Δt = 20m,
货车可以继续前进的时间为t₁ = t - Δt = 2s。
货车司机反应后立即加速,整车恰好完全通过时有最小的加速度,设其大小为a₁,则货车的位移满足L₁ + L₂ - Δx = v₀t₁ + $\frac{1}{2}$a₁t₁²,
解得a₁ = 3m/s²。
若汽车司机反应后立即减速,车头恰好到达阳台正下方时有最小的加速度,设其大小为a₂,则货车的位移满足
L₂ - Δx = v₀t₁ - $\frac{1}{2}$a₂t₁²,
解得a₂ = 1m/s²。
所以货车司机立即加速,且加速度大于等于3m/s²
或立即减速,且加速度大于等于1m/s²时,才能避险。
(1)花盆从82m的高处落下,到达离地高2m的车顶,根据位移公式有
h = $\frac{1}{2}$gt² = (82 - 2)m = 80m,
代入数据解得t = 4s。
花盆落到车顶时的速度大小为v = gt = 40m/s。
(2)货车司机反应时间内通过的距离为
Δx = v₀Δt = 20m,
货车可以继续前进的时间为t₁ = t - Δt = 2s。
货车司机反应后立即加速,整车恰好完全通过时有最小的加速度,设其大小为a₁,则货车的位移满足L₁ + L₂ - Δx = v₀t₁ + $\frac{1}{2}$a₁t₁²,
解得a₁ = 3m/s²。
若汽车司机反应后立即减速,车头恰好到达阳台正下方时有最小的加速度,设其大小为a₂,则货车的位移满足
L₂ - Δx = v₀t₁ - $\frac{1}{2}$a₂t₁²,
解得a₂ = 1m/s²。
所以货车司机立即加速,且加速度大于等于3m/s²
或立即减速,且加速度大于等于1m/s²时,才能避险。
#### 任务二 追及、相遇问题
活动1:有资料表明驾驶员的正常反应时间为0.3 - 0.8s,刹车时机动车的加速度一般为5.0 - 8.0m/s²。结合以上数据,请通过计算来说明车速为每小时100km时,安全距离为100m的理论依据。
活动2:假设在直线公路上A车以vA = 30m/s的速度匀速行驶,因大雾天气能见度低,当司机发现正前方有一辆同向匀速运动的B车时,两车距离仅有x0 = 92m,此时B车的速度vB = 10m/s,A车司机立即刹车(不计反应时间)而做匀减速直线运动,加速度大小为2m/s²(两车均视为质点),通过计算判断A是否会撞上B车。若会撞上,求A车从开始刹车到撞上B车的时间(假设B车一直匀速)。
活动1:有资料表明驾驶员的正常反应时间为0.3 - 0.8s,刹车时机动车的加速度一般为5.0 - 8.0m/s²。结合以上数据,请通过计算来说明车速为每小时100km时,安全距离为100m的理论依据。
活动2:假设在直线公路上A车以vA = 30m/s的速度匀速行驶,因大雾天气能见度低,当司机发现正前方有一辆同向匀速运动的B车时,两车距离仅有x0 = 92m,此时B车的速度vB = 10m/s,A车司机立即刹车(不计反应时间)而做匀减速直线运动,加速度大小为2m/s²(两车均视为质点),通过计算判断A是否会撞上B车。若会撞上,求A车从开始刹车到撞上B车的时间(假设B车一直匀速)。
答案:
活动1 提示:汽车速度v₀ = 100km/h ≈ 27.8m/s,
当驾驶员反应时间t₀ = 0.8s,刹车加速度a = -5.0m/s²时,刹车距离最长,此时驾驶员反应时间内
x₁ = v₀t₀ = 27.8×0.8m = 22.24m。
反应时间过后开始做匀减速直线运动,有
v² - v₀² = 2ax₂。
其中v = 0,代入数据解得x₂ = 77.28m。
故驾驶员从反应到刹车停止运动的位移大小为x = x₁ + x₂ = 99.52m。
故车速为每小时100km时,应当与同车道前车至少保持100m的距离。
活动2 提示:设两车速度相等的时间为t₀,则有vₐ - aₐt₀ = v_b,解得t₀ = 10s。
此时A车的位移xₐ = vₐt₀ - $\frac{1}{2}$aₐt₀² = 200m,
B车的位移x_b = v_b t₀ = 100m。
因为xₐ > x_b + 92m,所以会撞上B车,设撞上B车的时间为t₁,则有
vₐt₁ - $\frac{1}{2}$aₐt₁² = 92m + v_b t₁,
解得t₁ = (10 + 2$\sqrt{2}$)s(舍去),t₁ = (10 - 2$\sqrt{2}$)s。故A车撞上B车的时间为t₁ = (10 - 2$\sqrt{2}$)s。
当驾驶员反应时间t₀ = 0.8s,刹车加速度a = -5.0m/s²时,刹车距离最长,此时驾驶员反应时间内
x₁ = v₀t₀ = 27.8×0.8m = 22.24m。
反应时间过后开始做匀减速直线运动,有
v² - v₀² = 2ax₂。
其中v = 0,代入数据解得x₂ = 77.28m。
故驾驶员从反应到刹车停止运动的位移大小为x = x₁ + x₂ = 99.52m。
故车速为每小时100km时,应当与同车道前车至少保持100m的距离。
活动2 提示:设两车速度相等的时间为t₀,则有vₐ - aₐt₀ = v_b,解得t₀ = 10s。
此时A车的位移xₐ = vₐt₀ - $\frac{1}{2}$aₐt₀² = 200m,
B车的位移x_b = v_b t₀ = 100m。
因为xₐ > x_b + 92m,所以会撞上B车,设撞上B车的时间为t₁,则有
vₐt₁ - $\frac{1}{2}$aₐt₁² = 92m + v_b t₁,
解得t₁ = (10 + 2$\sqrt{2}$)s(舍去),t₁ = (10 - 2$\sqrt{2}$)s。故A车撞上B车的时间为t₁ = (10 - 2$\sqrt{2}$)s。
#### 任务三 逐差法的理解及应用
活动1:在“测量小车的加速度”的实验中,使小车从静止开始做匀加速直线运动,打点计时器的打点周期为T,打出的纸带如图所示,0、1、2、3是纸带上所取的部分计数点。

设初速度为v0,则前1T内、2T内、3T内……的位移分别为
x1 = v0T + $\frac{1}{2}$aT²,
x2 = v0·2T + $\frac{4}{2}$aT²,
x3 = v0·3T + $\frac{9}{2}$aT²,
……
所以第一个T内、第二个T内、第三个T内……的位移分别为
xⅠ = x1 = ________________,
xⅡ = x2 - x1 = ________________,
xⅢ = x3 - x2 = ________________,
则有xⅡ - xⅠ = ________,xⅢ - xⅡ = ________
所以Δx = xⅡ - xⅠ = xⅢ - xⅡ = ________。
活动2:如图所示的是某同学测量做直线运动的物体的瞬时速度时得到的一条纸带(实验中交流电源的频率为50Hz),依照打点的先后顺序取计数点1、2、3、4、5、6、7,相邻两计数点间还有4个点未画出,测得x1 = 1.42cm,x2 = 1.91cm,x3 = 2.40cm,x4 = 2.91cm,x5 = 3.43cm,x6 = 3.92cm。
(1)打第2个计数点时纸带的速度大小v2 = ________m/s(结果保留两位有效数字)。
(2)小车的加速度大小a = ________m/s²(结果保留两位有效数字)。
活动1:在“测量小车的加速度”的实验中,使小车从静止开始做匀加速直线运动,打点计时器的打点周期为T,打出的纸带如图所示,0、1、2、3是纸带上所取的部分计数点。

设初速度为v0,则前1T内、2T内、3T内……的位移分别为
x1 = v0T + $\frac{1}{2}$aT²,
x2 = v0·2T + $\frac{4}{2}$aT²,
x3 = v0·3T + $\frac{9}{2}$aT²,
……
所以第一个T内、第二个T内、第三个T内……的位移分别为
xⅠ = x1 = ________________,
xⅡ = x2 - x1 = ________________,
xⅢ = x3 - x2 = ________________,
则有xⅡ - xⅠ = ________,xⅢ - xⅡ = ________
所以Δx = xⅡ - xⅠ = xⅢ - xⅡ = ________。
活动2:如图所示的是某同学测量做直线运动的物体的瞬时速度时得到的一条纸带(实验中交流电源的频率为50Hz),依照打点的先后顺序取计数点1、2、3、4、5、6、7,相邻两计数点间还有4个点未画出,测得x1 = 1.42cm,x2 = 1.91cm,x3 = 2.40cm,x4 = 2.91cm,x5 = 3.43cm,x6 = 3.92cm。
(1)打第2个计数点时纸带的速度大小v2 = ________m/s(结果保留两位有效数字)。
(2)小车的加速度大小a = ________m/s²(结果保留两位有效数字)。
答案:
活动1 T + $\frac{1}{2}$aT² T + $\frac{3}{2}$aT² T + $\frac{5}{2}$aT² aT² aT² aT²
活动2 提示:
(1)打第2个计数点时纸带的速度大小为
v₂ = $\frac{x₁ + x₂}{2T}$ = $\frac{(1.42 + 1.91)×10^{-2}}{2×0.1}$m/s ≈ 0.17m/s。
(2)根据Δx = aT²,小车的加速度大小为
a = $\frac{x₄ + x₅ + x₆ - x₁ - x₂ - x₃}{(3T)²}$ ≈ 0.50m/s²。
活动2 提示:
(1)打第2个计数点时纸带的速度大小为
v₂ = $\frac{x₁ + x₂}{2T}$ = $\frac{(1.42 + 1.91)×10^{-2}}{2×0.1}$m/s ≈ 0.17m/s。
(2)根据Δx = aT²,小车的加速度大小为
a = $\frac{x₄ + x₅ + x₆ - x₁ - x₂ - x₃}{(3T)²}$ ≈ 0.50m/s²。
#### 活动达标
1. 做匀减速直线运动的物体经4s后停止运动,若在第1s内的位移是14m,则其最后1s内的位移是( )
A. 3.5m
B. 2m
C. 1m
D. 0
1. 做匀减速直线运动的物体经4s后停止运动,若在第1s内的位移是14m,则其最后1s内的位移是( )
A. 3.5m
B. 2m
C. 1m
D. 0
答案:
B解析:可把物体的运动看成反向的初速度为0的匀加速直线运动,由推论知在连续相等时间内的位移之比为1:3:5:7,已知第4s内的位移是14m,得第1s内的位移是2m,即在最后1s内物体的位移是2m,选项B正确。
2. 一辆小汽车以30m/s的速度匀速行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车突然失灵。如图所示,图线a、b分别为小汽车和大卡车的v - t图像(忽略刹车反应时间)。以下说法正确的是( )
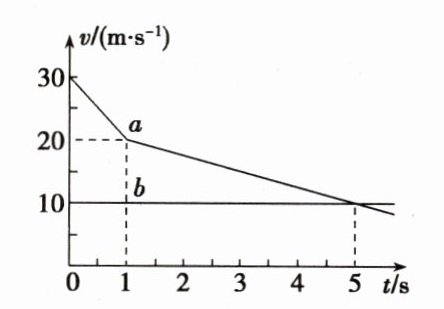
A. 因刹车失灵前小汽车已减速,故不会发生追尾事故
B. 在t = 3s时发生追尾事故
C. 在t = 5s时发生追尾事故
D. 若紧急刹车时两车相距40m,则不会发生追尾事故,且两车最近时相距10m

A. 因刹车失灵前小汽车已减速,故不会发生追尾事故
B. 在t = 3s时发生追尾事故
C. 在t = 5s时发生追尾事故
D. 若紧急刹车时两车相距40m,则不会发生追尾事故,且两车最近时相距10m
答案:
B 解析:根据速度 - 时间图像与时间轴所围“面积”的大小等于位移大小,由题图知,t = 3s时大卡车的位移为x_b = v_b t = 10×3m = 30m,小汽车的位移为xₐ = $\frac{1}{2}$×(30 + 20)×1m + $\frac{1}{2}$×(20 + 15)×2m = 60m,则xₐ - x_b = 30m,所以在t = 3s时发生追尾事故,故B正确,A、C错误;由v - t图像可知在t = 5s时两车速度相等,小汽车相对于大卡车的位移Δx = $\frac{1}{2}$×(20 + 10)×1m + $\frac{1}{2}$×10×4m = 35m < 40m,则不会发生追尾事故,两车最近时相距Δs = x₀ - Δx = 5m,故D错误。
3. 建筑工人常常徒手向上抛砖块,当砖块上升到最高点时被楼上的师傅接住。在一次抛砖的过程中,砖块运动3s到达最高点,将砖块的运动视为匀变速直线运动,砖块通过第2s内位移的后$\frac{1}{3}$用时为t1,通过第1s内位移的前$\frac{1}{5}$用时为t2,则$\frac{t2}{t1}$满足( )
A. $\frac{1}{5}$<$\frac{t2}{t1}$<$\frac{1}{4}$
B. $\frac{1}{4}$<$\frac{t2}{t1}$<$\frac{1}{3}$
C. $\frac{1}{3}$<$\frac{t2}{t1}$<$\frac{1}{2}$
D. $\frac{1}{2}$<$\frac{t2}{t1}$<1
A. $\frac{1}{5}$<$\frac{t2}{t1}$<$\frac{1}{4}$
B. $\frac{1}{4}$<$\frac{t2}{t1}$<$\frac{1}{3}$
C. $\frac{1}{3}$<$\frac{t2}{t1}$<$\frac{1}{2}$
D. $\frac{1}{2}$<$\frac{t2}{t1}$<1
答案:
3.C解析:竖直向上抛出后,砖块做匀变速直线运动,经过3s速度减为0,可以运用逆向思维,把上升过程反过来看作自由落体运动。根据自由落体运动的公式h = $\frac{1}{2}$gt²,得第1s内、第2s内、第3s内的位移之比为h₁:h₂:h₃ = 1:3:5。设第1s内位移为x,则第2s内位移为3x,第3s内位移为5x。所以砖块上抛过程中第2s内位移的后$\frac{1}{3}$的位移为自由落体运动中的第2个x,上抛过程中第1s内位移的前$\frac{1}{5}$的位移即为自由落体运动中的第9个x,按照自由落体运动公式可得t₁ = $\sqrt{\frac{2×2x}{g}}$ - $\sqrt{\frac{2x}{g}}$,t₂ = $\sqrt{\frac{2×9x}{g}}$ - $\sqrt{\frac{2×8x}{g}}$,所以$\frac{t₂}{t₁}$ = $\frac{\sqrt{9} - \sqrt{8}}{\sqrt{2} - 1}$ ≈ 0.41,所以A、B、D错误,C正确。
4. (多选)高铁已经成为我国重要的交通运输工具,某同学在乘坐高铁时,为研究自身所乘列车的运动情况,采用每隔相同时间T,记录列车外面的电线杆个数的方式来进行研究。假设列车做匀变速直线运动,相邻两电线杆的距离都为d。若从某线杆开始计时并记为“第1杆”,T时刻恰好记录“第3杆”,2T时刻恰好记录“第6杆”,3T时刻恰好记录“第10杆”。根据他记录的信息,下列判断正确的是( )
A. 开始记录时列车速度为0
B. 4T时刻恰好记录“第15杆”
C. 列车运动的加速度为$\frac{d}{T²}$
D. 2T时刻列车的速度为$\frac{5d}{2T}$
A. 开始记录时列车速度为0
B. 4T时刻恰好记录“第15杆”
C. 列车运动的加速度为$\frac{d}{T²}$
D. 2T时刻列车的速度为$\frac{5d}{2T}$
答案:
4.BC 解析:根据初速度为0的匀加速直线运动位移公式x = $\frac{1}{2}$at²可知,从开始运动时起,相邻相等时间内的位移之比为1:3:5:...:(2n - 1),而由题意可知,列车从开始记录起,前三个相邻T时间内的位移之比为(3 - 1)d:(6 - 3)d:(10 - 6)d = 2:3:4,所以开始记录时列车的速度不为0,故A错误;列车在相邻两个T时间内的位移之差均为Δx = d = aT²,则列车运动的加速度为a = $\frac{d}{T²}$,且由前面分析可推知列车第四个T时间内的位移为5d,则4T时刻恰好记录“第15杆”,故B、C正确;在2T时刻,列车的速度等于从T时和3T时之间的平均速度,即v₂_T = $\frac{(10 - 3)d}{2T}$ = $\frac{7d}{2T}$,故D错误。
5. (2022·全国乙卷)用雷达探测一高速飞行器的位置。从某时刻(t = 0)开始的一段时间内,该飞行器可视为沿直线运动,每隔1s测量一次其位置,坐标为x,结果如下表所示:
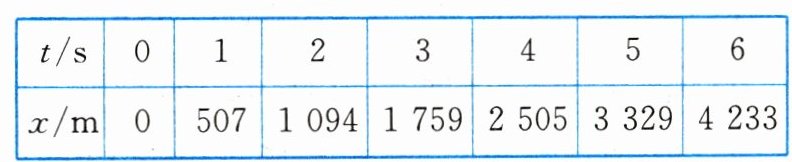
回答下列问题:
(1)根据表中数据可判断该飞行器在这段时间内近似做匀加速运动,判断的理由是:______________________________。
(2)当x = 507m时,该飞行器速度的大小v = ________m/s。
(3)这段时间内该飞行器加速度的大小a = ________m/s²(结果保留两位有效数字)。

回答下列问题:
(1)根据表中数据可判断该飞行器在这段时间内近似做匀加速运动,判断的理由是:______________________________。
(2)当x = 507m时,该飞行器速度的大小v = ________m/s。
(3)这段时间内该飞行器加速度的大小a = ________m/s²(结果保留两位有效数字)。
答案:
解析:
(1)根据表中数据可知,飞行器在每1s内的位移依次为507m,587m,665m,746m,824m,904m,则相邻1s内的位移之差接近Δx = 80m,可判断飞行器在这段时间内近似做匀加速运动。
(2)当x = 507m时飞行器的速度等于0~2s
内的平均速度,则v = $\frac{1094}{2}$m/s = 547m/s。
(3)a = $\frac{Δx}{9T²}$ = $\frac{4233 - 2×1759}{9×1²}$m/s² ≈ 79m/s²。
答案:
(1)相邻1s内的位移之差近似为一定值,接近Δx = 80m
(2)547
(3)79
(1)根据表中数据可知,飞行器在每1s内的位移依次为507m,587m,665m,746m,824m,904m,则相邻1s内的位移之差接近Δx = 80m,可判断飞行器在这段时间内近似做匀加速运动。
(2)当x = 507m时飞行器的速度等于0~2s
内的平均速度,则v = $\frac{1094}{2}$m/s = 547m/s。
(3)a = $\frac{Δx}{9T²}$ = $\frac{4233 - 2×1759}{9×1²}$m/s² ≈ 79m/s²。
答案:
(1)相邻1s内的位移之差近似为一定值,接近Δx = 80m
(2)547
(3)79
6. 一自行车以6m/s的速度沿平直的公路匀速运动,一汽车从静止开始与自行车同向做匀加速运动,加速度大小为3m/s²;汽车开始运动时,自行车恰好与汽车车头相齐。
(1)汽车追上自行车之前经多长时间两者相距最远?最远距离是多少?
(2)汽车经过多长时间追上自行车?此时汽车的速度是多少?
(1)汽车追上自行车之前经多长时间两者相距最远?最远距离是多少?
(2)汽车经过多长时间追上自行车?此时汽车的速度是多少?
答案:
解析:
(1)因汽车做匀加速运动,速度从0开始增加,但只要汽车的速度小于自行车的速度,两者的距离便不断增大,当两者速度相等时,距离最大。设相距最远的时间为t₁,则有
t₁ = $\frac{v}{a}$ = $\frac{6}{3}$s = 2s,
由x = $\frac{1}{2}$at²得x = $\frac{1}{2}$×3×2²m = 6m。
自行车的位移x₁ = vt₁ = 6×2m = 12m。
两者的最大距离xₘ = x₁ - x = 6m。
(2)设汽车经过时间t₂追上自行车,此时两者位移相等,则有$\frac{1}{2}$at₂² = vt₂,即$\frac{1}{2}$×3m/s²×t₂² = 6m/s×t₂。
解得t₂ = 4s(另一解不合题意,舍去)。
此时汽车的速度v₁ = at₂ = 3×4m/s = 12m/s。
答案:
(1)2s 6m
(2)4s 12m/s
(1)因汽车做匀加速运动,速度从0开始增加,但只要汽车的速度小于自行车的速度,两者的距离便不断增大,当两者速度相等时,距离最大。设相距最远的时间为t₁,则有
t₁ = $\frac{v}{a}$ = $\frac{6}{3}$s = 2s,
由x = $\frac{1}{2}$at²得x = $\frac{1}{2}$×3×2²m = 6m。
自行车的位移x₁ = vt₁ = 6×2m = 12m。
两者的最大距离xₘ = x₁ - x = 6m。
(2)设汽车经过时间t₂追上自行车,此时两者位移相等,则有$\frac{1}{2}$at₂² = vt₂,即$\frac{1}{2}$×3m/s²×t₂² = 6m/s×t₂。
解得t₂ = 4s(另一解不合题意,舍去)。
此时汽车的速度v₁ = at₂ = 3×4m/s = 12m/s。
答案:
(1)2s 6m
(2)4s 12m/s
7. 如图甲所示,A车原来临时停在一水平路面上,B车在后面匀速向A车靠近,A车司机发现后启动A车,以A车司机发现B车为计时起点(t = 0),A、B两车的v - t图像如图乙所示。已知B车在第1s内与A车的距离缩短了x1 = 12m。
(1)求B车运动的速度vB和A车的加速度a的大小。
(2)若A、B两车不会相撞,则A车司机发现B车时(t = 0)两车的距离x0应满足什么条件?

(1)求B车运动的速度vB和A车的加速度a的大小。
(2)若A、B两车不会相撞,则A车司机发现B车时(t = 0)两车的距离x0应满足什么条件?

答案:
解析:
(1)在t₁ = 1s时,A车刚启动,两车间缩短的距离x₁ = v_b t₁,
代入数据解得B车的速度v_b = 12m/s。
A车的加速度a = $\frac{v_b}{t₂ - t₁}$,
代入数据解得A车的加速度大小a = 3m/s²。
(2)两车的速度相等时,两车间的距离达到最小值,对应于v - t图像的t₂ = 5s时刻,此时两车已发生的相对位移为梯形部分的面积,即
x = $\frac{1}{2}$v_b (t₁ + t₂),解得x = 36m。
因此,若A、B两车不会相撞,则两车的距离x₀ 应满足条件x₀ > 36m。
答案:
(1)12m/s 3m/s²
(2)x₀ > 36m
(1)在t₁ = 1s时,A车刚启动,两车间缩短的距离x₁ = v_b t₁,
代入数据解得B车的速度v_b = 12m/s。
A车的加速度a = $\frac{v_b}{t₂ - t₁}$,
代入数据解得A车的加速度大小a = 3m/s²。
(2)两车的速度相等时,两车间的距离达到最小值,对应于v - t图像的t₂ = 5s时刻,此时两车已发生的相对位移为梯形部分的面积,即
x = $\frac{1}{2}$v_b (t₁ + t₂),解得x = 36m。
因此,若A、B两车不会相撞,则两车的距离x₀ 应满足条件x₀ > 36m。
答案:
(1)12m/s 3m/s²
(2)x₀ > 36m
8. 中国细犬(简称细犬)是中国古老的狩猎犬种,主要分布在山东省内。某次狩猎细犬发现正南方L = 24m处有一只野兔,野兔也发现细犬并立刻向正南方逃跑,同时细犬向正南方沿直线追击野兔。已知细犬的加速度为a1 = 4m/s²,最大速度为v1 = 16m/s;野兔的加速度为a2 = 8m/s²,最大速度为v2 = 8m/s。
(1)求细犬和野兔之间的最大距离。
(2)经过多长时间,细犬捕获野兔?
(3)若野兔发现细犬后,向正东方逃跑,细犬迅速判断(不计判断时间)并沿某方向直线追击拦截野兔,正好将其捕获,则经过多长时间,细犬捕获野兔?
(1)求细犬和野兔之间的最大距离。
(2)经过多长时间,细犬捕获野兔?
(3)若野兔发现细犬后,向正东方逃跑,细犬迅速判断(不计判断时间)并沿某方向直线追击拦截野兔,正好将其捕获,则经过多长时间,细犬捕获野兔?
答案:
解析:
(1)野兔最大速度为v₂ = 8m/s,
加速到最大速度的时间t₀ = $\frac{v₂}{a₂}$ = 1s,
加速到最大速度时的位移x₀ = $\frac{v₂²}{2a₂}$ = 4m。
当细犬的速度和野兔速度相等时两者距离最大,则经过的时间t₁ = $\frac{v₂}{a₁}$ = 2s,
此时细犬和野兔之间的最大距离为
xₘ = L + x₀ + v₂(t₁ - t₀) - $\frac{1}{2}$a₁t₁² = 28m。
(2)细犬加速到最大速度的时间t = $\frac{v₁}{a₁}$ = 4s。加速到最大速度时的位移x = $\frac{v₁²}{2a₁}$ = 32m。
假设细犬在加速阶段追上兔子,且经过的时间为t,则
$\frac{1}{2}$a₁t² = L + x₀ + v₂(t - t₀),
解得t = 5.7s > 4s(另一值舍掉)。
则假设不成立,细犬将在匀速阶段追上兔子,有x + v₁(t - t) = L + x₀ + v₂(t - t₀),
解得t = 6.5s。
(3)由题意可知[x + v₁(t' - t)]² = L² + [x₀ + v₂(t' - t₀)]²。
由细犬追上野兔时,细犬的位移必须大于野兔的位移,当t ≤ 2s时,野兔的位移大于细犬的位移,故追上时一定有t > 2s。
当2s < t < 4s时,24² + [4 + (t - 1)×8]² = ($\frac{1}{2}$×4×t²)²无解。
当t ≥ 4s时,24² + [4 + (t - 1)×8]² = [32 + (t - 4)×16]²,解得t = 4.5s。
综上,经过4.5s后,细犬捕获野兔。
答案:
(1)28m
(2)6.5s
(3)4.5s
(1)野兔最大速度为v₂ = 8m/s,
加速到最大速度的时间t₀ = $\frac{v₂}{a₂}$ = 1s,
加速到最大速度时的位移x₀ = $\frac{v₂²}{2a₂}$ = 4m。
当细犬的速度和野兔速度相等时两者距离最大,则经过的时间t₁ = $\frac{v₂}{a₁}$ = 2s,
此时细犬和野兔之间的最大距离为
xₘ = L + x₀ + v₂(t₁ - t₀) - $\frac{1}{2}$a₁t₁² = 28m。
(2)细犬加速到最大速度的时间t = $\frac{v₁}{a₁}$ = 4s。加速到最大速度时的位移x = $\frac{v₁²}{2a₁}$ = 32m。
假设细犬在加速阶段追上兔子,且经过的时间为t,则
$\frac{1}{2}$a₁t² = L + x₀ + v₂(t - t₀),
解得t = 5.7s > 4s(另一值舍掉)。
则假设不成立,细犬将在匀速阶段追上兔子,有x + v₁(t - t) = L + x₀ + v₂(t - t₀),
解得t = 6.5s。
(3)由题意可知[x + v₁(t' - t)]² = L² + [x₀ + v₂(t' - t₀)]²。
由细犬追上野兔时,细犬的位移必须大于野兔的位移,当t ≤ 2s时,野兔的位移大于细犬的位移,故追上时一定有t > 2s。
当2s < t < 4s时,24² + [4 + (t - 1)×8]² = ($\frac{1}{2}$×4×t²)²无解。
当t ≥ 4s时,24² + [4 + (t - 1)×8]² = [32 + (t - 4)×16]²,解得t = 4.5s。
综上,经过4.5s后,细犬捕获野兔。
答案:
(1)28m
(2)6.5s
(3)4.5s
查看更多完整答案,请扫码查看


