《2025年随堂小考七年级数学下册北师大版》

1. 如图，$AB = AC$，$DB = DC$，则直接由“SSS”可以判定 ( )

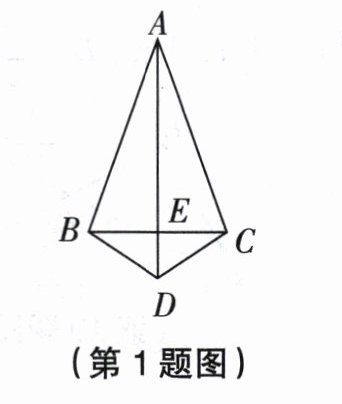
A. $\triangle ABD\cong\triangle ACD$ B. $\triangle ABE\cong\triangle ACE$
C. $\triangle EBD\cong\triangle ECD$ D. 以上答案都不对

答案： A

2. 如图，已知$AC = AD$，$BC = BD$，$CE = DE$，则图中全等三角形共有 ( )

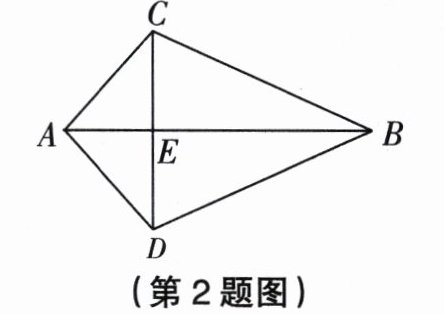
A. 1对 B. 2对 C. 3对 D. 4对

答案： C

3. 如图，木工师傅做好门框后，为防止变形，常常像图中所示那样钉上两根斜拉的木条(即图中的$AB$，$CD$两根木条)，这样做的数学原理是 ( )

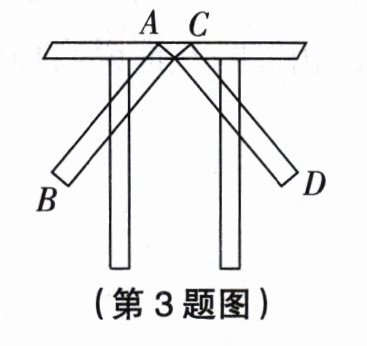
A. 两点确定一条直线 B. 两点之间，线段最短
C. 美学原理 D. 三角形的稳定性

答案： D

4. 用尺规作图，已知三边作三角形，用到的基本作图是 ( )
A. 作一个角等于已知角
B. 作已知直线的垂线
C. 作一条线段等于已知线段
D. 作角的平分线

答案： C

5. 如图，$AD$，$BC$交于点$O$，$AC = BD$，$AO = BO$，$CO = DO$，$\angle D = 30^{\circ}$，$\angle A = 95^{\circ}$，则$\angle AOB$等于 ( )

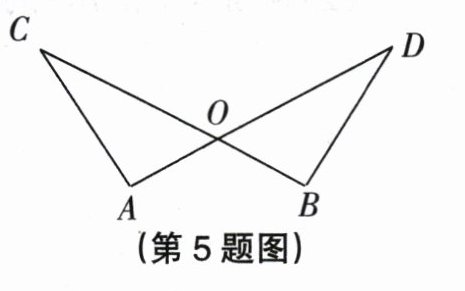
A. $120^{\circ}$ B. $125^{\circ}$
C. $130^{\circ}$ D. $135^{\circ}$

答案： B

6. 如图，$OA = OB$，$AC = BC$，$\angle ACO = 30^{\circ}$，则$\angle ACB =$______.

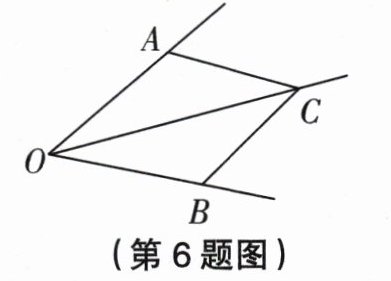
答案： 60°

7. 如图，$AB = DE$，$AC = DF$，$BE = CF$，$\angle A = 60^{\circ}$，则$\angle D =$______.

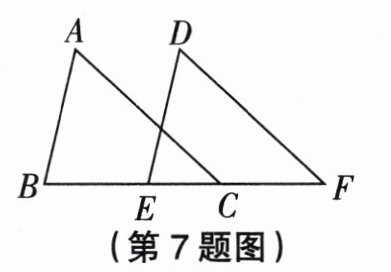
答案： 60°

8. 如图，在$\triangle ACD$和$\triangle BCE$中，$AD$与$BE$交于点$P$. 若$AC = BC$，$AD = BE$，$CD = CE$，$\angle ACE = 55^{\circ}$，$\angle BCD = 155^{\circ}$，则$\angle APB$的度数为______.

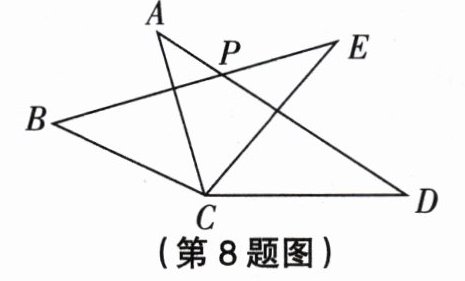
答案： 50°