《2024年新课程课堂同步练习册九年级数学上册人教版》

2. 张大爷要围成一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为32米的篱笆恰好围成,围成的花圃是如图3所示的矩形ABCD.设AB边长为x米,矩形ABCD的面积为S平方米.
(1)求S与x之间的函数解析式;(不要求写出自变量x的取值范围)
(2)当x为何值时,S有最大值?并求出最大值.

答案： 解：
(1)S=x(32-2x)=-2{x}^{2}+32x
(2)S=-2{x}^{2}+32x
        =-2({x}^{2}-16x)
        =-2{(x-8)}^{2}+128
∴当x=8时，S取最大值，最大值为128

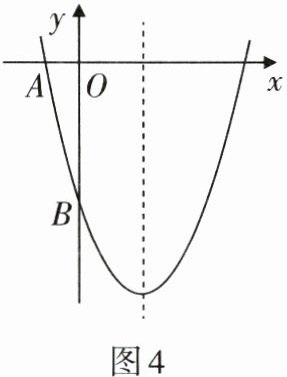
3. 如图4,已知二次函数$y= ax^{2}-4x+c(a≠0)的图象与坐标轴交于点A(-1,0)和点B(0,-5)$.
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得$\triangle ABP$的周长最小. 请求出点P的坐标.

答案： 解：
(1)将A(-1，0)和B(0，-5)代入y=a{x}^{2}-4x+c中，得
$ {{\begin{cases} {{a×{(-1)}^{2}-4×(-1)+c=0}} \\ {c=-5} \end{cases}}}$
解得，${{\begin{cases} {{a=1}} \\ {c=-5} \end{cases}}}$
∴二次函数的解析式为y={x}^{2}-4x-5
(2)设函数图象与x轴的另一个交点为点C，连接BC，
则BC与对称轴的交点即为点P．
∵二次函数的解析式为y={x}^{2}-4x-5
∴函数图象的对称轴为直线x=2
令{x}^{2}-4x-5=0，解得$x_1=5，$$x_2=-1$
∴点C的坐标为(5，0)
∵点B的坐标为(0，-5)
∴直线BC的解析式为y=x-5
当x=2时，y=2-5=-3
∴点P的坐标为(2，-3)