8. 如图5,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连接AE. 若∠BCD= 2∠BAD,则∠DAE的度数是( )
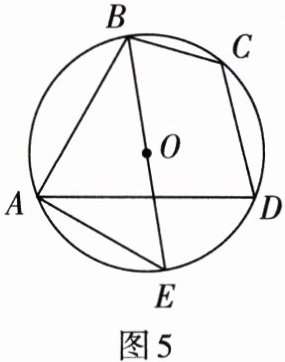
A.30°
B.35°
C.45°
D.60°

A.30°
B.35°
C.45°
D.60°
答案:
A
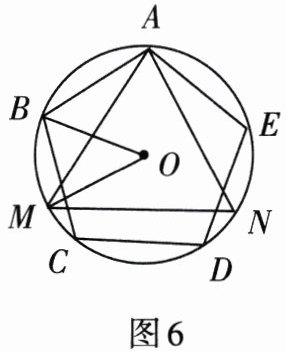
1. 如图6,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM= ______.
答案:
48°
2. 若圆锥的底面半径是2 cm,母线长是4 cm,则圆锥的侧面积是______$cm^2$(结果保留π).
答案:
8π
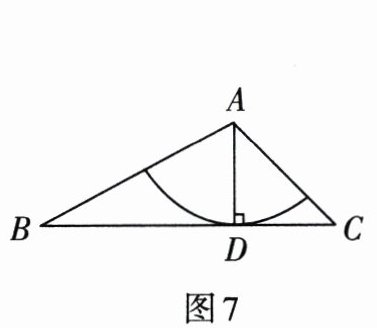
3. 如图7,在△ABC中,AB= 2,AC= $\sqrt{2}$,以A为圆心,1为半径的圆与边BC相切于点D,则∠BAC的度数是______度.



答案:
105
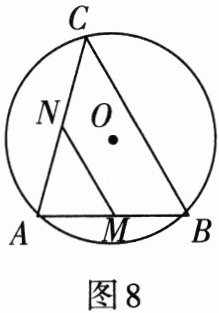
4. 如图8,AB是⊙O的弦,AB= 5,点C是⊙O上的一个动点,且∠ACB= 45°. 若点M,N分别是AB,AC的中点,则MN的最大值是______.
答案:
$\frac {5\sqrt {2}}2$
1. 已知:如图9,P是△ABC的内心,过P点作△ABC的外接圆的弦AE,交BC于D点.
求证:(1)∠BAE= ∠EBC;(2)BE= PE.
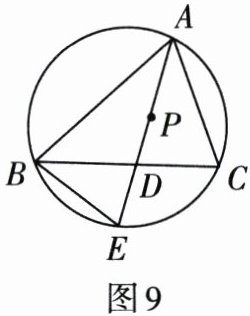
求证:(1)∠BAE= ∠EBC;(2)BE= PE.

答案:
证明:
(1)
∵P是△ABC的内心
∴AP平分∠BAC
∴∠BAE=∠CAE
∵∠CAE和∠CBE都是$\widehat{CE}$所对圆周角
∴∠CAE=∠CBE
∴∠BAE=∠CBE
(2)连接BP,
∵P是△ABC的内心
∴BP平分∠ABC
∴∠ABP=∠CBP
∵∠BPE=∠ABP+∠BAE,∠PBE=∠CBP+∠CBE
∴∠BPE=∠PBE
∴BE=PE
(1)
∵P是△ABC的内心
∴AP平分∠BAC
∴∠BAE=∠CAE
∵∠CAE和∠CBE都是$\widehat{CE}$所对圆周角
∴∠CAE=∠CBE
∴∠BAE=∠CBE
(2)连接BP,
∵P是△ABC的内心
∴BP平分∠ABC
∴∠ABP=∠CBP
∵∠BPE=∠ABP+∠BAE,∠PBE=∠CBP+∠CBE
∴∠BPE=∠PBE
∴BE=PE
查看更多完整答案,请扫码查看


