2. 如图10,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径. 求证:∠BAM= ∠CAP.


答案:
证明:连接BM,
∵AM是⊙O的直径
∴∠ABM=90°
∵AP⊥BC
∴∠APC=90°
∵∠AMB和∠ACB都是$\widehat{AB}$所对圆周角
∴∠AMB=∠ACB
∴90°-∠AMB=90°-∠ACB,即∠BAM=∠CAP
∵AM是⊙O的直径
∴∠ABM=90°
∵AP⊥BC
∴∠APC=90°
∵∠AMB和∠ACB都是$\widehat{AB}$所对圆周角
∴∠AMB=∠ACB
∴90°-∠AMB=90°-∠ACB,即∠BAM=∠CAP
3. 已知等腰三角形ABC内接于半径为6 cm的⊙O,AB= AC,点O到BC的距离OD的长等于2 cm.求AB的长.
答案:
解:①如图, 连接AD,连接OB,
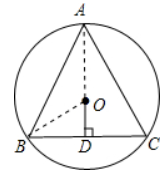
∵△ABC是等腰三角形,
∴根据等腰三角形的性质(三线合一定理)得出,AO⊥BC,AO平分BC,
∵OD⊥BC,
∴根据垂直定理得:OD平分BC, 即A、O、D三点共线,
∴AO过D,
∵等腰△ABC内接于半径为$6\ \mathrm {cm}$的⊙O,
∴$OA=6\ \mathrm {cm},$BD=DC,AD⊥BC,
在Rt△OBD中,由勾股定理得:$BD=\sqrt{OB^2-OD^2}=\sqrt{6^2-2^2}=4\sqrt{2}(\ \mathrm {cm}),$
在Rt△ADB中,由勾股定理得:$AB=\sqrt{AD^2+BD^2}=\sqrt{(6+2)^2+(4\sqrt{2})^2}=4\sqrt{6}(\ \mathrm {cm}),$
②如图: 同法求出$BD=4\sqrt{2}\ \mathrm {cm},$$AD=6\ \mathrm {cm}-2\ \mathrm {cm}=4\ \mathrm {cm},$
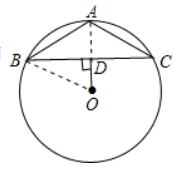
由勾股定理得:$AB=\sqrt{AD^2+BD^2}=\sqrt{(4\sqrt{2})^2+4^2}=4\sqrt{3}(\ \mathrm {cm}),$
答:AB的长是$4\sqrt{6}\ \mathrm {cm}$或$4\sqrt{3}\ \mathrm {cm}$
解:①如图, 连接AD,连接OB,

∵△ABC是等腰三角形,
∴根据等腰三角形的性质(三线合一定理)得出,AO⊥BC,AO平分BC,
∵OD⊥BC,
∴根据垂直定理得:OD平分BC, 即A、O、D三点共线,
∴AO过D,
∵等腰△ABC内接于半径为$6\ \mathrm {cm}$的⊙O,
∴$OA=6\ \mathrm {cm},$BD=DC,AD⊥BC,
在Rt△OBD中,由勾股定理得:$BD=\sqrt{OB^2-OD^2}=\sqrt{6^2-2^2}=4\sqrt{2}(\ \mathrm {cm}),$
在Rt△ADB中,由勾股定理得:$AB=\sqrt{AD^2+BD^2}=\sqrt{(6+2)^2+(4\sqrt{2})^2}=4\sqrt{6}(\ \mathrm {cm}),$
②如图: 同法求出$BD=4\sqrt{2}\ \mathrm {cm},$$AD=6\ \mathrm {cm}-2\ \mathrm {cm}=4\ \mathrm {cm},$

由勾股定理得:$AB=\sqrt{AD^2+BD^2}=\sqrt{(4\sqrt{2})^2+4^2}=4\sqrt{3}(\ \mathrm {cm}),$
答:AB的长是$4\sqrt{6}\ \mathrm {cm}$或$4\sqrt{3}\ \mathrm {cm}$
查看更多完整答案,请扫码查看


