1.含有三个实数的集合可表示为{a,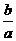 ,1},也可表示为{a2,
a+b,0},则a2006+b2006 的值为
,1},也可表示为{a2,
a+b,0},则a2006+b2006 的值为
( )
A.0 B.1 C.-1 D.±1
20. (本小题满分15分)
已知抛物线
 的对称轴为y轴,且与x轴相切,又知抛物线的焦点为
的对称轴为y轴,且与x轴相切,又知抛物线的焦点为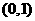 .
.
(Ⅰ) 求抛物线的方程;(3分)
(Ⅱ)过该抛物线的的对称轴上任一点P(0,m)(m>0)作直线与抛物线交第一象限于点A,交第二象限于点B,点Q是点P关于原点的对称点,设点P分有向线段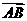 所成的比为λ,试判断
所成的比为λ,试判断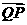 与
与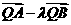 是否互相垂直?(7分)
是否互相垂直?(7分)
(Ⅲ) 设直线AB的方程是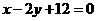 ,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.(5分)
,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.(5分)
19.(本小题满分14分)
已知函数f(x)的定义域为R,对任意的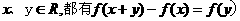 ,且当
,且当 时,
时,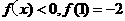 .
.
(Ⅰ)求证:函数f(x)为奇函数;(3分)
(Ⅱ)求证: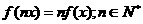 (5分)
(5分)
(Ⅲ)求函数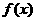 在区间[-n,n](n
在区间[-n,n](n )上的最大值和最小值。(6分)
)上的最大值和最小值。(6分)
18. (本小题满分14分)
甲、乙两人比赛远距离投篮,规定每人最多投5次,谁先投中谁胜(如二人在同次都投中,则为和局,比赛结束)已知甲每次投中的概率为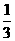 ,乙每次投中的概率为
,乙每次投中的概率为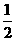 ,且每次是否投中,相互之间没有影响。
,且每次是否投中,相互之间没有影响。
(Ⅰ)求第一轮分出胜负的概率;(两人都投一次称为一轮)(3分)
(Ⅱ)求第二轮分出胜负的概率;(4分)
(Ⅲ)求乙获胜地概率。(7分)
17. (本小题满分13分)
(本小题满分13分)
已知正方体ABCD-A1B1C1D1的棱长为a,M是棱AA1的中点,
点O是对角线BD1的中点。
(Ⅰ)求证:OM是AA1和BD1的公垂线;(6分)
(Ⅱ) 过该正方体对角线BD1作截面分别交棱AA1、CC1于点P、
Q,试求截面D1PBQ面积的最小值; (7分)
14.函数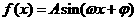
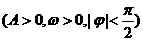 的部分图象如图所示,则有下列命题:
的部分图象如图所示,则有下列命题:
 ①函数f(x)的最小正周期为
①函数f(x)的最小正周期为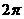 ;
;
②直线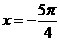 是函数f(x)的图象的一条对称轴;
是函数f(x)的图象的一条对称轴;
③点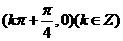 是函数f(x)图象的对称中心;
是函数f(x)图象的对称中心;
④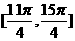 是函数f(x)的一个单调增区间.
是函数f(x)的一个单调增区间.
其中正确的命题序号是 .

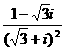 等于 ( )
等于 ( )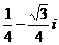 B.
B.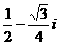 C.
C.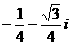 D.
D.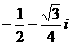
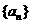 的前n项和为
的前n项和为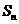 ,且向量
,且向量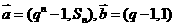 共线
共线 。
。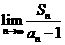 的值。(6分)
的值。(6分) B={x||x-2|<a},若
B={x||x-2|<a},若 (B
(B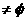 ),求实数a的取值范围.
),求实数a的取值范围.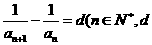 为常数),则称数列
为常数),则称数列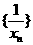 为调和数列,且
为调和数列,且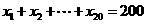 ,则
,则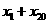 =
、
=
、 的最大值为
。
的最大值为
。