18、(本小题满分14分)
设函数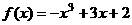 分别在
分别在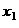 、
、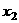 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为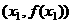 、
、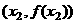 ,该平面上动点P满足
,该平面上动点P满足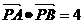 ,点Q是点P关于直线
,点Q是点P关于直线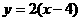 的对称点.求(Ⅰ)点A、B的坐标 ;
的对称点.求(Ⅰ)点A、B的坐标 ;
(Ⅱ)动点Q的轨迹方程
18解: (Ⅰ)令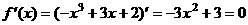 解得
解得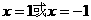
当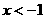 时,
时,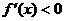 , 当
, 当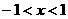 时,
时,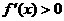 ,当
,当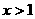 时,
时,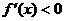
所以,函数在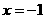 处取得极小值,在
处取得极小值,在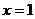 取得极大值,故
取得极大值,故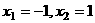 ,
,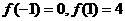
所以, 点A、B的坐标为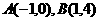 .
.
(Ⅱ) 设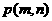 ,
,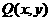 ,
,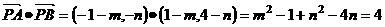
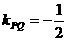 ,所以
,所以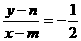 ,又PQ的中点在
,又PQ的中点在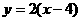 上,所以
上,所以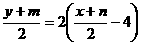
消去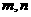 得
得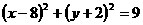
17、解:(Ⅰ)∵AD与两圆所在的平面均垂直,
∴AD⊥AB, AD⊥AF,故∠BAD是二面角B-AD-F的平面角,
依题意可知,ABCD是正方形,所以∠BAD=450.
即二面角B-AD-F的大小为450;
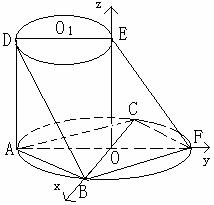
(Ⅱ)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0,0,0),A(0,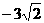 ,0),B(
,0),B(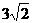 ,0,0),D(0,
,0,0),D(0,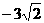 ,8),E(0,0,8),F(0,
,8),E(0,0,8),F(0,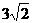 ,0)
,0)
 所以,
所以,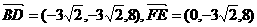
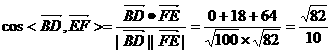
设异面直线BD与EF所成角为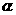 ,则
,则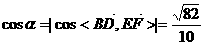
直线BD与EF所成的角为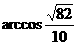
17、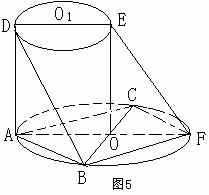 (本小题满分14分)
(本小题满分14分)
如图5所示,AF、DE分别是⊙O、⊙O1的直径.AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE//AD.
(Ⅰ)求二面角B-AD-F的大小;
(Ⅱ)求直线BD与EF所成的角.
16、(本小题满分12分)
某运动员射击一次所得环数X的分布列如下:
|
X |
0-6 |
7 |
8 |
9 |
10 |
|
Y |
0 |
0.2 |
0.3 |
0.3 |
0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为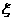 .
.
(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求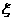 分布列;
分布列;
(Ⅲ) 求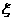 的数学希望.
的数学希望.
16解:(Ⅰ)求该运动员两次都命中7环的概率为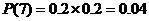 ;
;
(Ⅱ)
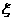 的可能取值为7、8、9、10
的可能取值为7、8、9、10
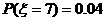
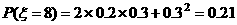
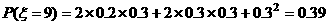
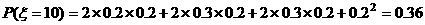
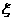 分布列为
分布列为
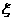 |
7 |
8 |
9 |
10 |
|
P |
0.04 |
0.21 |
0.39 |
0.36 |
(Ⅲ) 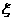 的数学希望为
的数学希望为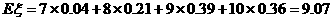 .
.
15、(本小题满分14分)
已知函数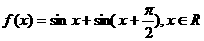
(Ⅰ)求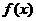 的最小正周期;
的最小正周期;
(Ⅱ)求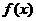 的最大值和最小值;
的最大值和最小值;
(Ⅲ)若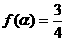 ,求
,求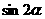 的值.
的值.
15解: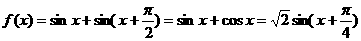
(Ⅰ)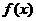 的最小正周期为
的最小正周期为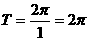 ;
;
(Ⅱ)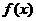 的最大值为
的最大值为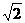 和最小值
和最小值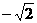 ;
;
(Ⅲ)因为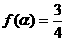 ,即
,即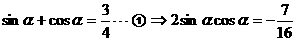 ,即
,即 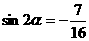
14、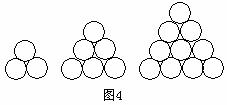 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图4所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图4所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以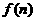 表示第n堆的乒乓球总数,则
表示第n堆的乒乓球总数,则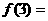 ;
;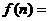 (答案用n表示) .
(答案用n表示) .

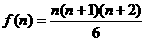
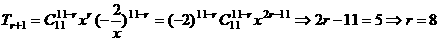
 的系数为
的系数为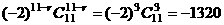
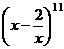 的展开式中,
的展开式中,
