科目:,来源:,题型:
20、(本题12分) 是定义在
是定义在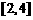 上且满足如下条件的函数
上且满足如下条件的函数 组成的集合:①对任意的
组成的集合:①对任意的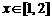 ,都有
,都有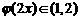 ;②存在常数
;②存在常数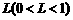 ,使得对任意的
,使得对任意的 ,都有
,都有 .
.
(I)设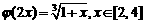 ,证明:
,证明:
(II)设 ,如果存在
,如果存在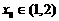 ,使得
,使得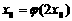 ,那么这样的
,那么这样的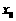 是唯一的;
是唯一的;
(III) 设 ,任取
,任取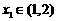 ,令
,令 ,
,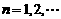 ,证明:给定正整数
,证明:给定正整数 ,对任意的正整数
,对任意的正整数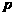 ,成立不等式
,成立不等式
高考 (B)
点击展开完整题目
试题详情
科目:,来源:,题型:
19、(本题14分)已知公比为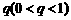 的无穷等比数列
的无穷等比数列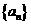 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列 各项的和为
各项的和为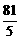 .
.
(I)求数列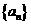 的首项
的首项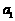 和公比
和公比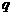 ;
;
(II)对给定的 ,设
,设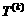 是首项为
是首项为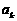 ,公差为
,公差为 的等差数列,求
的等差数列,求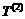 的前10项之和;
的前10项之和;
(III)设 为数列
为数列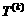 的第
的第 项,
项,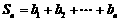 ,求
,求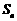 ,并求正整数
,并求正整数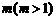 ,使得
,使得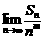 存在且不等于零.
存在且不等于零.
(注:无穷等比数列各项的和即当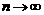 时该无穷等比数列前
时该无穷等比数列前 项和的极限)
项和的极限)
点击展开完整题目
试题详情
科目:,来源:,题型:
18、(本题14分)设函数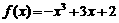 分别在
分别在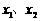 处取得极小值、极大值.
处取得极小值、极大值. 平面上点
平面上点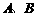 的坐标分别为
的坐标分别为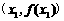 、
、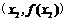 ,该平面上动点
,该平面上动点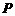 满足
满足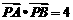 ,点
,点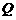 是点
是点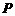 关于直线
关于直线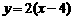 的对称点.求
的对称点.求
(I)求点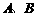 的坐标;
的坐标;
(II)求动点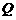 的轨迹方程.
的轨迹方程.
点击展开完整题目
试题详情
科目:,来源:,题型:
16、(本题12分)某运动员射击一次所得环数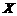 的分布如下:
的分布如下:
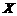 |
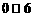 |
7 |
8 |
9 |
10 |
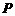 |
0 |
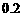 |
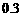 |
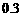 |
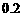 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为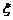 .
.
(I)求该运动员两次都命中7环的概率
(II)求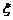 的分布列
的分布列
(III) 求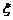 的数学期望
的数学期望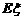 .
.
点击展开完整题目
试题详情
科目:,来源:,题型:
14、 在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第
在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第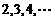 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第 堆第
堆第 层就放一个乒乓球,以
层就放一个乒乓球,以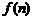 表示第
表示第 堆的乒乓球总数,则
堆的乒乓球总数,则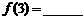 ;
; (答案用
(答案用 表示).
表示).
三解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
点击展开完整题目
试题详情

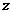 满足方程
满足方程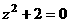 ,则
,则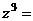
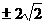 B.
B. 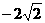 C.
C. 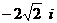 D.
D.
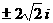
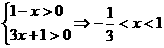 ,故选B.
,故选B. 的定义域是
的定义域是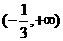 B.
B. 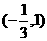 C.
C.  D.
D.
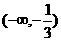
 (本题14分)如图5所示,
(本题14分)如图5所示,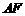 、
、 分别世
分别世 、
、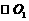 的直径,
的直径, 与两圆所在的平面均垂直,
与两圆所在的平面均垂直,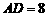 .
. 是
是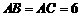 ,
,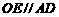 .
. 的大小;
的大小;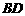 与
与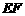 所成的角.
所成的角. .
. 的最小正周期;
的最小正周期;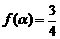 ,求
,求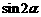 的值.
的值.