18. (本小题满分12分)
(本小题满分12分)
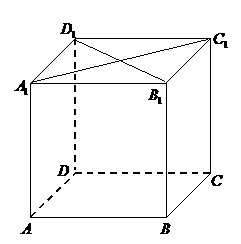
如图,在棱长为1的正方体 中,
中,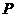 是侧棱
是侧棱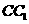 上的一点,
上的一点,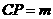 。
。
(Ⅰ)、试确定 ,使直线
,使直线 与平面
与平面 所成角的正切值为
所成角的正切值为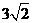 ;
;
 (Ⅱ)、在线段
(Ⅱ)、在线段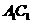 上是否存在一个定点Q,使得对任意的
上是否存在一个定点Q,使得对任意的 ,D1Q在平面
,D1Q在平面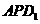 上的射影垂直于
上的射影垂直于 ,并证明你的结论。
,并证明你的结论。
点评:本小题主要考查线面关系、直线于平面所成的角的有关知识及空间想象能力和推理运算能力,考查运用向量知识解决数学问题的能力。
解法1:(Ⅰ)连AC,设AC与BD相交于点O,AP与平面 相交于点,,连结OG,因为
相交于点,,连结OG,因为
PC∥平面 ,平面
,平面 ∩平面APC=OG,
∩平面APC=OG,
故OG∥PC,所以,OG=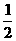 PC=
PC=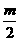 .
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面 ,
,
故∠AGO是AP与平面 所成的角.
所成的角.
在Rt△AOG中,tanAGO= ,即m=
,即m= .
.
所以,当m= 时,直线AP与平面
时,直线AP与平面 所成的角的正切值为
所成的角的正切值为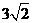 .
.
(Ⅱ)可以推测,点Q应当是AICI的中点O1,因为
D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP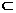 平面ACC1A1,故 D1O1⊥AP.
平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。
17.(本小题满分13分)
已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为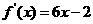 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点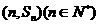 均在函数
均在函数 的图像上。
的图像上。
(Ⅰ)、求数列 的通项公式;
的通项公式;
(Ⅱ)、设 ,
,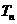 是数列
是数列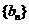 的前n项和,求使得
的前n项和,求使得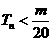 对所有
对所有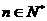 都成立的最小正整数m;
都成立的最小正整数m;
点评:本小题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力。
解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点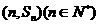 均在函数
均在函数 的图像上,所以
的图像上,所以 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-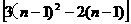 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (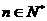 )
)
(Ⅱ)由(Ⅰ)得知 =
=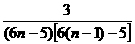 =
= ,
,
故Tn= =
=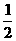
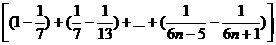 =
=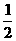 (1-
(1- ).
).
因此,要使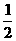 (1-
(1- )<
)< (
(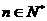 )成立的m,必须且仅须满足
)成立的m,必须且仅须满足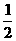 ≤
≤ ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
16.(本小题满分12分)
设函数 ,其中向量
,其中向量 ,
,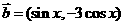 ,
, ,
,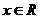 。
。
(Ⅰ)、求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)、将函数 的图像按向量
的图像按向量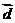 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的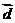 。
。
点评:本小题主要考查平面向量数量积的计算方法、三角公式、三角函数的性质及图像的基本知识,考查推理和运算能力。
解:(Ⅰ)由题意得,f(x)=a·(b+c)=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+ sin(2x+
sin(2x+ ).
).
所以,f(x)的最大值为2+ ,最小正周期是
,最小正周期是 =
= .
.
(Ⅱ)由sin(2x+ )=0得2x+
)=0得2x+ =k.
=k. ,即x=
,即x=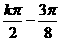 ,k∈Z,
,k∈Z,
于是d=(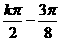 ,-2),
,-2), k∈Z.
k∈Z.
因为k为整数,要使 最小,则只有k=1,此时d=(―
最小,则只有k=1,此时d=(― ,―2)即为所求.
,―2)即为所求.
14.某工程队有6项工程需要单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,有工程丁必须在工程丙完成后立即进行。那么安排这6项工程的不同排法种数是 20 。(用数字作答)
10.关于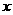 的方程
的方程 ,给出下列四个命题: ( A )
,给出下列四个命题: ( A )
①存在实数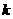 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数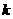 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数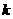 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数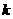 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.1 C.2 D.3
第Ⅱ卷(非选择题 共100分)
第Ⅱ卷用0.5毫米黑色的签字笔或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。
9.已知平面区域D由以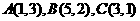 为顶点的三角形内部&边界组成。若在区域D上有无穷多个点
为顶点的三角形内部&边界组成。若在区域D上有无穷多个点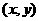 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则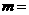 (C )
(C )
A.-2 B.-1 C.1 D.4

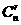 都换成
都换成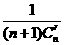 ,就得到一个如右图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出
,就得到一个如右图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出 ,其中
,其中 r+1 。令
r+1 。令 ,则
,则 。
。 与圆
与圆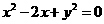 相切,则
相切,则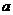 的值为 -18或8 。
的值为 -18或8 。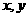 为实数,且
为实数,且 ,则
,则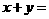 4 。
4 。