科目:,来源:,题型:
8.有限集合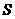 中元素的个数记做
中元素的个数记做 ,设
,设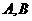 都为有限集合,给出下列命题:
都为有限集合,给出下列命题:
①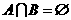 的充要条件是
的充要条件是 ;
;
②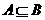 的充要条件是
的充要条件是 ;
;
③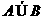 的充要条件是
的充要条件是 ;
;
④ 的充要条件是
的充要条件是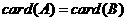 ;
;
其中真命题的序号是 ( B )
A.③④ B.①② C.①④ D.②③
点击展开完整题目
试题详情
科目:,来源:,题型:
6.关于直线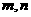 与平面
与平面 ,有以下四个命题:
,有以下四个命题:
①若 且
且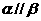 ,则
,则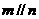 ;
;
②若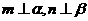 且
且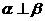 ,则
,则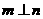 ;
;
③若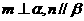 且
且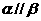 ,则
,则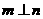 ;
;
④若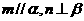 且
且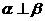 ,则
,则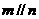 ;
;
其中真命题的序号是 ( D )
A.①② B.③④ C.①④ D.②③
点击展开完整题目
试题详情
科目:,来源:,题型:
20、(本小题满分12分)
A是由定义在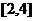 上且满足如下条件的函数
上且满足如下条件的函数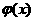 组成的集合:①对任意
组成的集合:①对任意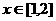 ,都有
,都有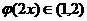 ; ②存在常数
; ②存在常数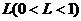 ,使得对任意的
,使得对任意的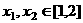 ,都有
,都有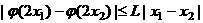
(Ⅰ)设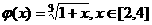 ,证明:
,证明: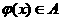
(Ⅱ)设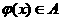 ,如果存在
,如果存在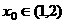 ,使得
,使得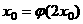 ,那么这样的
,那么这样的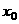 是唯一的;
是唯一的;
(Ⅲ)设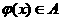 ,任取
,任取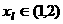 ,令
,令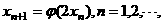 证明:给定正整数k,对任意的正整数p,成立不等式
证明:给定正整数k,对任意的正整数p,成立不等式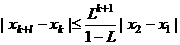
解:对任意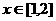 ,
,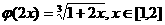 ,
,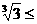
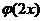
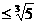 ,
,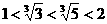 ,所以
,所以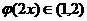
对任意的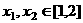 ,
,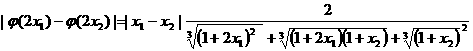 ,
,
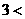
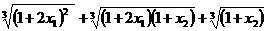 ,所以0<
,所以0<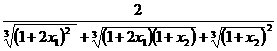
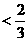 ,令
,令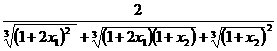 =
=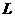 ,
,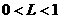 ,
,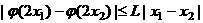
所以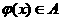
反证法:设存在两个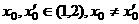 使得
使得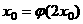 ,
,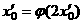 则
则
由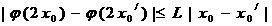 ,得
,得 ,所以
,所以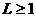 ,矛盾,故结论成立。
,矛盾,故结论成立。
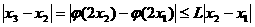 ,所以
,所以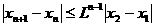
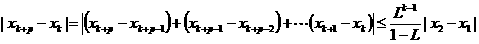
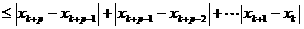

 +…
+…
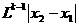
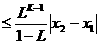
点击展开完整题目
试题详情
科目:,来源:,题型:
19、(本小题满分14分)
已知公比为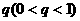 的无穷等比数列
的无穷等比数列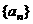 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列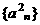 各项的和为
各项的和为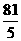 .
.
(Ⅰ)求数列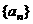 的首项
的首项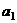 和公比
和公比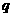 ;
;
(Ⅱ)对给定的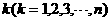 ,设
,设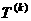 是首项为
是首项为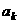 ,公差为
,公差为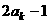 的等差数列.求数列
的等差数列.求数列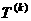 的前10项之和;
的前10项之和;
(Ⅲ)设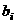 为数列
为数列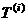 的第
的第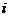 项,
项,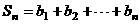 ,求
,求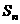 ,并求正整数
,并求正整数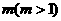 ,使得
,使得
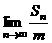 存在且不等于零.
存在且不等于零.
(注:无穷等比数列各项的和即当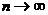 时该无穷数列前n项和的极限)
时该无穷数列前n项和的极限)
19解: (Ⅰ)依题意可知,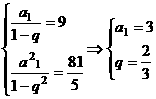
(Ⅱ)由(Ⅰ)知,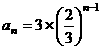 ,所以数列
,所以数列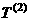 的的首项为
的的首项为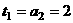 ,公差
,公差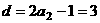 ,
,
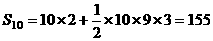 ,即数列
,即数列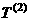 的前10项之和为155.
的前10项之和为155.
(Ⅲ) 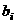 =
=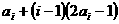 =
=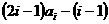 =
=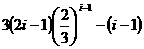 ,
,
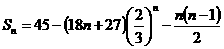 ,
,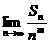 =
=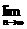
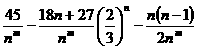
当m=2时,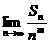 =-
=-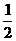 ,当m>2时,
,当m>2时,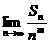 =0,所以m=2
=0,所以m=2
点击展开完整题目
试题详情

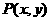 的直线分别与
的直线分别与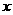 轴的正半轴和
轴的正半轴和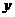 轴的正半轴交于
轴的正半轴交于 与点
与点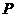 关于
关于 为坐标原点,若
为坐标原点,若 且
且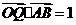 ,则点
,则点 B.
B.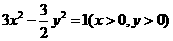
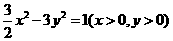 D.
D.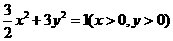
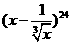 的展开式中,
的展开式中,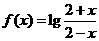 ,则
,则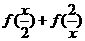 的定义域为
( B )
的定义域为
( B ) B.
B.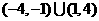
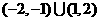 D.
D.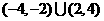
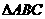 的内角
的内角 满足
满足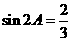 ,则
,则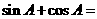 ( A )
( A )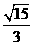 B.
B.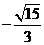 C.
C.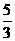 D.
D.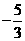
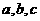 成等差数列,
成等差数列,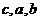 成等比数列,且
成等比数列,且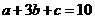 ,则
,则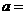 ( D )
( D )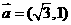 ,
,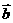 是不平行于
是不平行于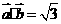 ,则
,则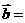 ( B )
( B )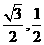 ) B.(
) B.(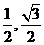 ) C.(
) C.( ) D.(
) D.(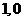 )
)