16.(本小题满分12分)
设函数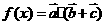 ,其中向量
,其中向量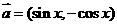 ,
,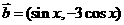 ,
,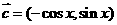 ,
, 。
。
(Ⅰ)、求函数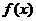 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)、将函数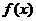 的图像按向量
的图像按向量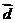 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的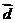 。
。
点评:本小题主要考查平面向量数量积的计算方法、三角公式、三角函数的性质及图像的基本知识,考查推理和运算能力。
解:(Ⅰ)由题意得,f(x)=a·(b+c)=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+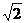 sin(2x+
sin(2x+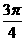 ).
).
所以,f(x)的最大值为2+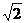 ,最小正周期是
,最小正周期是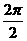 =
=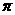 .
.
(Ⅱ)由sin(2x+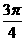 )=0得2x+
)=0得2x+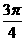 =k.
=k.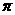 ,即x=
,即x=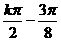 ,k∈Z,
,k∈Z,
于是d=(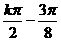 ,-2),
,-2),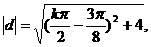 k∈Z.
k∈Z.
因为k为整数,要使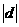 最小,则只有k=1,此时d=(―
最小,则只有k=1,此时d=(―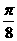 ,―2)即为所求.
,―2)即为所求.
- 答案

