科目:,来源:,题型:
20.解:⑴ ∵
∴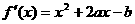 由题意
由题意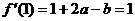
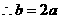 ……①
3分
……①
3分
∵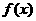 有极值,∴方程
有极值,∴方程 有两个不等实根.
有两个不等实根.
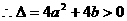
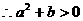 ……②
……②
由①、②可得,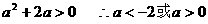 .
.
故实数a的取值范围是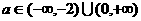 6分
6分
⑵存在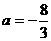 ,
7分
,
7分
由⑴可知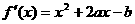 ,令
,令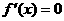 ,
,
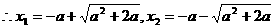
|
x |
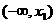 |
x1 |
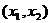 |
x2 |
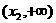 |
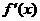 |
+ |
0 |
- |
0 |
+ |
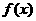 |
单调增 |
极大值 |
单调减 |
极小值 |
单调增 |
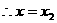 时,
时,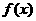 取极小值, 9分
取极小值, 9分
则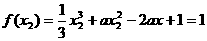 ,
, 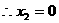 或
或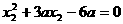 ,
,
若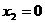 ,即
,即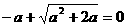 ,则
,则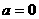 (舍) 11分
(舍) 11分
若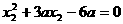 ,又
,又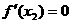 ,
,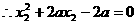 ,
,
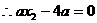 ,
,  ,
,
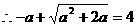
 ,
,
∴存在实数a =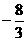 ,使得函数
,使得函数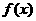 的极小值为1. 14分
的极小值为1. 14分
点击展开完整题目
试题详情
科目:,来源:,题型:
19.解:⑴ 当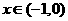 时,有
时,有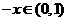 ,
,
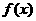 是偶函数
是偶函数
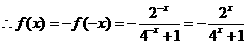 2分
2分
由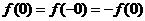 得
得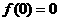 ,
,
又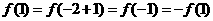 得
得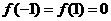 , 5分
, 5分
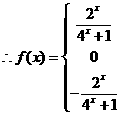
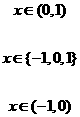 6分
6分
⑵ 当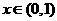 时,有
时,有 ,
,
任取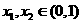 且
且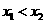
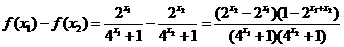 8分
8分
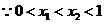 ,
,
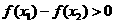 即
即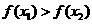

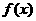 在
在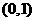 上是减函数. 10分
上是减函数. 10分
⑶ 由于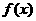 在
在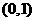 上是减函数,
上是减函数,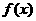 在
在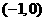 上是减函数
上是减函数
当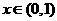 时,有
时,有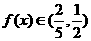 ,
,
当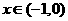 时,有
时,有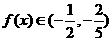 ,
,
当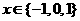 时,有
时,有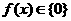 , 13分
, 13分
 当
当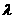
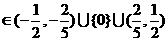 时,方程
时,方程 在
在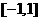 上有实数解. 14分
上有实数解. 14分
点击展开完整题目
试题详情
科目:,来源:,题型:
17.解:⑴ 当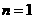 时,
时,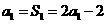 ,
, 1分
1分
当 时,
时, ,
, , 2分
, 2分
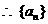 是以
是以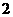 为首项,以
为首项,以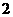 为公比的等比数列.
为公比的等比数列.  4分
4分
由于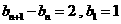 , 5分
, 5分
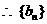 是以
是以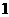 为首项,以
为首项,以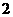 为公差的等差数列.
为公差的等差数列. 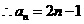 7分
7分
⑵ 由⑴知: ,
,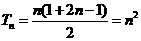 9分
9分
现在只要证明:当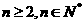 时,
时,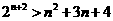 ,用数学归纳法证明:
,用数学归纳法证明:
(I)当 时,有左边=
时,有左边=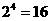 ,右边=
,右边= ,不等式成立 10分
,不等式成立 10分
(II)假设当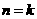 时,不等式成立,即
时,不等式成立,即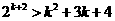 ,
,
那么当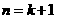 时,有
时,有

当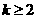 时,恒有
时,恒有 成立,
成立,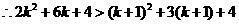
即

 当
当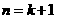 时,不等式也成立 13分
时,不等式也成立 13分
由(I)、(II)知,当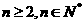 时, 有
时, 有 . 14分
. 14分
点击展开完整题目
试题详情

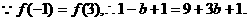
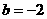 .(或利用对称性求解)
3分
.(或利用对称性求解)
3分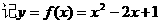

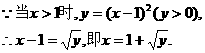
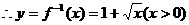 .
7分
.
7分
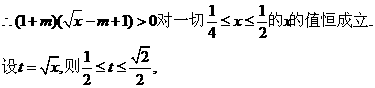
 9分
9分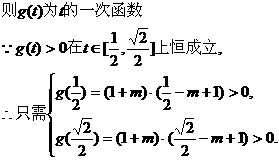
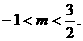 13分
13分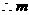 的取值范围是:
的取值范围是: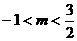 .
14分
.
14分
 3分
3分
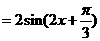 3分
3分 7分
7分
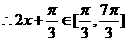 9分
9分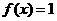 得:
得: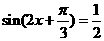 ,
, 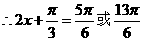 12分
12分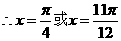 14分
14分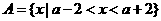 , 3分
, 3分 得,
得,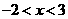 , 6分
, 6分 7分
7分
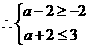 10分
10分
 12分
12分  14分
14分 12.
12. 13.
13. 14.
14.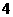


 三山高级中学
三山高级中学 高三理科第一次月考数学卷参考答案
高三理科第一次月考数学卷参考答案