2.条件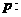
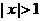 ,条件
,条件
 ,则
,则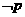 是
是 的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.充分但不必要条件 B.必要但不充分条件
C.充分且必要条件 D.既不充分也不必要条件
21、(本小题满分14分)
已知二次函数f(x)满足f(-1)=0,且 8x f(x)
f(x) 4(x2+1) 对
4(x2+1) 对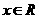 恒成立
恒成立
(1)求函数y=f(x)的解析式;
(2)利用函数g(x)= 的定义域为D,构造一个数列{xn},方法如下:
的定义域为D,构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= g(x1),x3=g(x2),…,xn= g(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域D中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
如果X1= ,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
19.(本小题满分14分)
已知点A(7,0)在曲线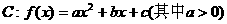 上,且曲线C在点A处的切线与直线
上,且曲线C在点A处的切线与直线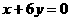 垂直,又当
垂直,又当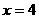 时,函数
时,函数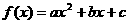 有最小值.
有最小值.
(I)求实数a,b,c的值;
(II)设函数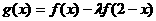 的最大值为M,
的最大值为M,
求正整数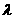 的值,使得
的值,使得 成立.
成立.
20(本小题满分14分)
函数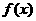 是定义域为R的偶函数,且对任意的
是定义域为R的偶函数,且对任意的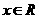 ,均有
,均有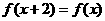 成立.当
成立.当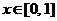 时,
时,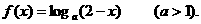
(1)当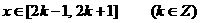 时,求
时,求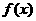 的表达式;
的表达式;
(2)若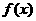 的最大值为
的最大值为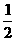 ,解关于x的不等式
,解关于x的不等式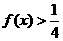 .
.
18. (本小题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,
讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随
后学生的注意力开始分散. 设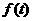 表示学生注意力随时间t(分钟)的变化规律(
表示学生注意力随时间t(分钟)的变化规律(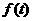
越大,表明学生注意力越集中),经过实验分析得知:
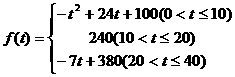
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)有一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么
老师能否在学生达到所需的状态下讲授完这道题目?若能,老师如何安排讲解时
间;若不能,说明理由.

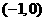 内的函数
内的函数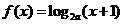 满足
满足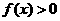 ,则实数
,则实数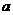 的取值范围为( )
的取值范围为( ) B.
B.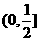 C.
C.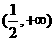 D.
D.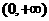
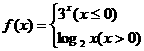 ,那么
,那么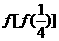 的值为┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的值为┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )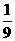 C.
C.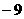 D.
D.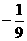
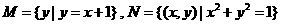 ,则集合
,则集合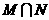 中元素的个数是┄┄( )
中元素的个数是┄┄( ) B.
B.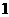 C.
C.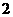 D.不确定
D.不确定 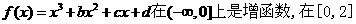 上是减函数,且
上是减函数,且 。
。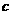 的值,并求出
的值,并求出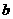 和
和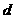 的取值范围。
的取值范围。 。
。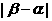 的取值范围,并写出当
的取值范围,并写出当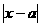 ,
,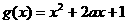 (a为正常数),
(a为正常数),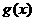 的图象在y轴上的截距相等.
的图象在y轴上的截距相等.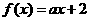 ,不等式
,不等式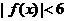 的解集为
的解集为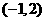 ,
,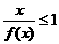 的解集
的解集