17.解:⑴ 当 时,
时, ,
,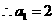 1分
1分
当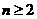 时,
时,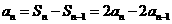 ,
,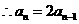 , 2分
, 2分
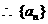 是以
是以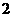 为首项,以
为首项,以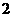 为公比的等比数列.
为公比的等比数列. 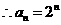 4分
4分
由于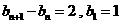 , 5分
, 5分
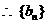 是以
是以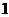 为首项,以
为首项,以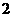 为公差的等差数列.
为公差的等差数列. 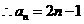 7分
7分
⑵ 由⑴知: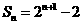 ,
,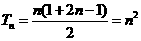 9分
9分
现在只要证明:当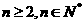 时,
时,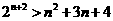 ,用数学归纳法证明:
,用数学归纳法证明:
(I)当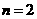 时,有左边=
时,有左边= ,右边=
,右边= ,不等式成立 10分
,不等式成立 10分
(II)假设当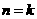 时,不等式成立,即
时,不等式成立,即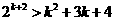 ,
,
那么当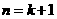 时,有
时,有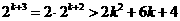
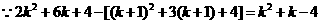
当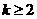 时,恒有
时,恒有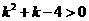 成立,
成立,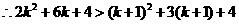
即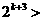
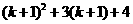
 当
当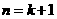 时,不等式也成立 13分
时,不等式也成立 13分
由(I)、(II)知,当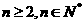 时, 有
时, 有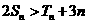 . 14分
. 14分
- 答案

