【题目】如图,矩形![]() 和菱形
和菱形![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() ,
,![]() ,
,![]() ,
,![]() .
.
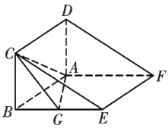
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)可证![]() 平面
平面![]() ,从而得到
,从而得到![]() ,又可证
,又可证![]() ,从而得到
,从而得到![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的法向量和面
的法向量和面![]() 的法向量后计算它们的夹角的余弦值,再结合二面角为钝角以及同角的三角函数基本关系式可求二面角的正切值.
的法向量后计算它们的夹角的余弦值,再结合二面角为钝角以及同角的三角函数基本关系式可求二面角的正切值.
(1)证明:∵矩形![]() 和菱形
和菱形![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() ,
,
∵矩形![]() 菱形
菱形![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵菱形![]() 中,
中,
![]() ,
,![]() ,
,![]() ,故
,故![]() ,
,
∴由勾股定理得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
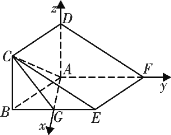
由已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,
,
则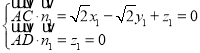 ,取
,取![]() 得
得![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则
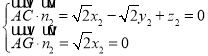 ,取
,取![]() 得
得![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() 且
且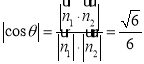 ,所以
,所以![]() ,
,
由![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的正切值为
的正切值为![]() .
.

