【题目】众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，因此被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”的一个示意图，整个图形是一个圆面，其中黑色区域在轴右侧部分的边界为一个半圆．给出以下命题：

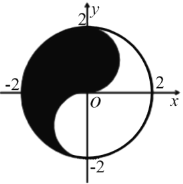
①在太极图中随机取一点，此点取自黑色部分的概率是；

②当时，直线与白色部分有公共点；

③黑色阴影部分中一点，则的最大值为2；

④设点，点在此太极图上，使得，的范围是．

其中所有正确结论的序号是（ ）

A.①②B.②③C.①③D.①④

【答案】D

【解析】

根据几何概型概率计算，判断①的正确性；

根据直线和圆的位置关系，判断②的正确性；

根据线性规划的知识求得的最大值，由此判断③的正确性；

将转化为过的两条切线所成的角大于等于，由此求得的取值范围，进而求得的取值范围，从而判断出④的正确性.

对于①，将y轴右侧黑色阴影部分补到左侧，即可知黑色阴影区域占圆的面积的一半，

根据几何概型的计算公式，所以在太极图中随机取一点，

此点取自黑色阴影部分的概率是，①正确；

对于②，当时，直线,

过点，所以直线与白色部分在第I和第IV象限部分没有

公共点.圆的圆心为，半径为，圆心到直线

，即直线的距离为，

所以直线与白色部分在第III象限的部分没有公共点.

综上所述，直线y＝ax+2a与白色部分没有公共点，②错误；

对于③，设l：z＝x+y，由线性规划知识可知，当直线l与圆x2+（y﹣1）2＝1相切时，

z最大，由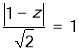解得z（舍去），③错误；

对于④，要使得∠OPQ＝45°，即需要过点P的两条切线所成角大于等于，

所以，即OP≤2，于是22+b2≤8，解得，④正确．

故选：D

关闭