《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版》

13. 已知椭圆 $ \Gamma:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1(a＞b＞0) $ 的长轴长是 4，离心率为 $ \frac{\sqrt{3}}{2} $.
(1) 求 $ \Gamma $ 的方程.
(2) 若点 $ P $ 是圆 $ O:x^{2}+y^{2} = 5 $ 上的一动点，过点 $ P $ 作 $ \Gamma $ 的两条切线分别交圆 $ O $ 于点 $ A $，$ B $.
（ⅰ）求证：$ PA\perp PB $.
（ⅱ）求 $ \triangle PAB $ 面积的取值范围.

答案： 13.椭圆的标准方程+圆的方程+直线与椭圆的位置关系
解:
(1)由题意得$\begin{cases} 2a = 4, \\ \frac{c}{a} = \frac{\sqrt{3}}{2}, \end{cases}$
所以$a = 2$，$c = \sqrt{3}$。
所以$b^{2} = 1$。
所以椭圆$\Gamma$的方程为$\frac{x^{2}}{4} + y^{2} = 1$。
(2)(ⅰ)证明:当直线$PA$，$PB$中有一条的斜率不存在时，不妨设$PA$的斜率不存在，
因为$PA$与椭圆只有一个公共点，
所以其方程为$x = \pm 2$。
当$PA$的方程为$x = 2$时，此时$PA$与圆的交点坐标为$(2,\pm 1)$，
此时$PB$的方程为$y = 1$(或$y = -1$)，$PA \perp PB$成立，
同理可证，当$PA$的方程为$x = -2$时，$PA \perp PB$成立(技巧:先用特殊情况探路，加深对问题的理解，同时为一般情况下的求解过程寻找思路)；
当直线$PA$，$PB$的斜率都存在时，
设点$P(m,n)$且$m^{2} + n^{2} = 5$。
设直线方程为$y = k(x - m) + n$，代入椭圆方程，
可得$(1 + 4k^{2})x^{2} + 8k(n - km)x + 4(n - km)^{2} - 4 = 0$，
由$\Delta = 0$化简整理得$(4 - m^{2})k^{2} + 2mnk + 1 - n^{2} = 0$。
因为$m^{2} + n^{2} = 5$，
所以$(4 - m^{2})k^{2} + 2mnk + m^{2} - 4 = 0$。
设$PA$，$PB$的斜率分别为$k_1$，$k_2$，
所以$k_1k_2 = -1$。
所以$PA \perp PB$成立(方法:以直线方程为参数式，与椭圆方程联立，设而不求，用判别式处理相切关系，构造出含有参数$k$，$m$，$n$的方程，利用点$P(m,n)$坐标中的参数$m$，$n$和关系式$m^{2} + n^{2} = 5$化简方程并消参，构造出关于斜率$k$的一元二次方程，再借助根与系数的关系得出$PA$，$PB$的斜率之积的关系，即可完成$PA \perp PB$的证明)。
(ⅱ)设坐标原点到直线$PA$，$PB$的距离分别为$d_1$，$d_2$。
因为$PA \perp PB$，所以$AB$是圆$O$的直径。
所以$PA = 2d_2$，$PB = 2d_1$，$d_1^{2} + d_2^{2} = OP^{2} = 5$(关键:利用圆的几何性质，得出距离平方之和为常数)。
则$\triangle PAB$的面积$S = \frac{1}{2}\vert PA\vert × \vert PB\vert = 2d_1d_2$，
$S^{2} = 4d_1^{2}d_2^{2} = 4d_1^{2}(5 - d_1^{2}) = -4d_1^{4} + 20d_1^{2}$(提示:写出$\triangle PAB$的面积表达式，利用$d_1^{2} + d_2^{2} = 5$消元，转化为二次函数，结合$d_1^{2}$的取值范围求出最值)。
因为$d_1^{2} \in [1,4]$，所以$S^{2} \in [16,25]$。
所以$\triangle PAB$面积的取值范围是$[4,5]$。

14. 设抛物线 $ C:y^{2} = 2px(p＞0) $，过焦点 $ F $ 的直线与抛物线 $ C $ 交于点 $ A(x_{1},y_{1}) $，$ B(x_{2},y_{2}) $. 当直线 $ AB $ 垂直于 $ x $ 轴时，$ |AB| = 2 $.

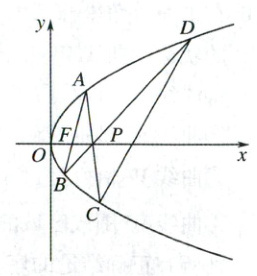
(1) 求抛物线 $ C $ 的标准方程.
(2) 已知点 $ P(1,0) $，直线 $ AP $，$ BP $ 分别与抛物线 $ C $ 交于点 $ C $，$ D $.
（ⅰ）求证：直线 $ CD $ 过定点.
（ⅱ）求 $ \triangle PAB $ 与 $ \triangle PCD $ 面积之和的最小值.

答案： 14.抛物线的标准方程+直线与抛物线的位置关系
解:
(1)由题知，直线$AB$过抛物线$C:y^{2} = 2px(p ＞ 0)$的焦点$F$，
当直线$AB$垂直于$x$轴时，$AB$为抛物线的通径，
所以$\vert AB\vert = 2p = 2$。解得$p = 1$，
所以抛物线$C$的标准方程为$y^{2} = 2x$。
(2)(ⅰ)证明:设点$C(x_3,y_3)$，$D(x_4,y_4)$，
直线$AB$的方程为$x = my + \frac{1}{2}$，
联立$\begin{cases} x = my + \frac{1}{2}, \\ y^{2} = 2x, \end{cases}$得$y^{2} - 2my - 1 = 0$，
所以$y_1 + y_2 = 2m$，$y_1y_2 = -1$。
设直线$AC$的方程为$x = ny + 1$，
联立$\begin{cases} x = ny + 1, \\ y^{2} = 2x, \end{cases}$得$y^{2} - 2ny - 2 = 0$，
所以$y_1 + y_3 = 2n$，$y_1y_3 = -2$。则$y_3 = \frac{-2}{y_1}$
同理可得$y_4 = \frac{-2}{y_2}$，
所以$k_{CD} = \frac{y_3 - y_4}{x_3 - x_4}=\frac{y_3 - y_4}{\frac{y_3^{2}}{2} - \frac{y_4^{2}}{2}} = \frac{2}{y_3 + y_4}=\frac{2}{\frac{-2}{y_1}+\frac{-2}{y_2}} = -\frac{y_1y_2}{y_1 + y_2}=\frac{1}{2m}$(关键:分别设$AB$，$AC$，$BD$的直线方程并与抛物线方程联立，结合根与系数的关系，得到$y_1y_3 = -2$，$y_2y_4 = -2$，进而化简得出$k_{CD} = \frac{y_3 - y_4}{x_3 - x_4} = \frac{1}{2m}$)。
因此直线$CD$的方程为$x = 2m(y - y_3) + x_3$。
由对称性知，定点在$x$轴上(提示:根据对称性确定定点在$x$轴上，将$y = 0$代入直线$CD$的方程，求出相应的$x$与定点坐标)。
令$y = 0$，得$x = -2my_3 + x_3 = -2my_3 + \frac{y_3^{2}}{2}=-2m·\frac{-2}{y_1}+\frac{(\frac{-2}{y_1})^{2}}{2}=\frac{4m}{y_1}+\frac{2}{y_1^{2}} = 2 + 2(\frac{y_2}{y_1}+\frac{1}{y_1^{2}})=2 + 2·\frac{y_1y_2 + 1}{y_1^{2}} = 2$，
所以直线$CD$过定点$Q(2,0)$。
(ⅱ)因为$S_{\triangle PAB} = \frac{1}{2}\vert PF\vert · \vert y_1 - y_2\vert = \frac{1}{4}\vert y_1 - y_2\vert$，
$S_{\triangle PCD} = \frac{1}{2}\vert PQ\vert · \vert y_3 - y_4\vert=\frac{1}{2}\vert\frac{-2}{y_1}-\frac{-2}{y_2}\vert=\vert\frac{1}{y_1}-\frac{1}{y_2}\vert=\frac{\vert y_1 - y_2\vert}{\vert y_1y_2\vert}=\vert y_1 - y_2\vert$，
所以$S_{\triangle PAB} + S_{\triangle PCD} = \frac{5}{4}\vert y_1 - y_2\vert=\frac{5}{4}\sqrt{(y_1 + y_2)^{2} - 4y_1y_2}=\frac{5}{4}\sqrt{4m^{2} + 4}=\frac{5}{2}\sqrt{m^{2} + 1} \geqslant \frac{5}{2}$，
当且仅当$m = 0$时等号成立。
所以$\triangle PAB$与$\triangle PCD$面积之和的最小值为$\frac{5}{2}$。