2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若直线 $ l $ 的一个方向向量为 $ \boldsymbol{a}=(1,0,2) $, 平面 $ \alpha $ 的一个法向量为 $ \boldsymbol{u}=(-2,0,-4) $, 则 (
A.$ l // \alpha $
B.$ l \perp \alpha $
C.$ l \subset \alpha $
D.$ l $ 与 $ \alpha $ 斜交
B
)A.$ l // \alpha $
B.$ l \perp \alpha $
C.$ l \subset \alpha $
D.$ l $ 与 $ \alpha $ 斜交
答案:
1.B【解析】空间向量的应用 由题可知$-2\overrightarrow{a}=(-2,0,-4)=\overrightarrow{u}$,所以$\overrightarrow{a}//\overrightarrow{u}$,即$l\perp\alpha$.故选B.
2. 若平面 $ \alpha_1, \alpha_2 $ 平行, 则下面可以是这两个平面的法向量的是 (
A.$ \boldsymbol{n}_1=(1,2,3), \boldsymbol{n}_2=(-3,2,1) $
B.$ \boldsymbol{n}_1=(1,2,2), \boldsymbol{n}_2=(-2,2,1) $
C.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-2,2,1) $
D.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-2,-2,-2) $
D
)A.$ \boldsymbol{n}_1=(1,2,3), \boldsymbol{n}_2=(-3,2,1) $
B.$ \boldsymbol{n}_1=(1,2,2), \boldsymbol{n}_2=(-2,2,1) $
C.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-2,2,1) $
D.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-2,-2,-2) $
答案:
2.D【解析】法向量 两个平面平行时其法向量也平行,检验知正确选项为D,故选D.
3. 若平面 $ \alpha_1, \alpha_2 $ 垂直, 则下面可以是这两个平面的法向量的是 (
A.$ \boldsymbol{n}_1=(1,2,1), \boldsymbol{n}_2=(-3,1,1) $
B.$ \boldsymbol{n}_1=(1,1,2), \boldsymbol{n}_2=(-2,1,1) $
C.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-1,2,1) $
D.$ \boldsymbol{n}_1=(1,2,1), \boldsymbol{n}_2=(0,-2,-2) $
A
)A.$ \boldsymbol{n}_1=(1,2,1), \boldsymbol{n}_2=(-3,1,1) $
B.$ \boldsymbol{n}_1=(1,1,2), \boldsymbol{n}_2=(-2,1,1) $
C.$ \boldsymbol{n}_1=(1,1,1), \boldsymbol{n}_2=(-1,2,1) $
D.$ \boldsymbol{n}_1=(1,2,1), \boldsymbol{n}_2=(0,-2,-2) $
答案:
3.A【解析】法向量 两个平面垂直时其法向量也垂直,只有选项A中的两个向量垂直,故选A.
4. 如图, 在长方体 $ ABCD - A_1B_1C_1D_1 $ 中, $ AB = AA_1 = 2, AD = 1 $, $ E $ 为 $ A_1B_1 $ 的中点, 点 $ P $ 满足 $ \overrightarrow{DP} = \lambda \overrightarrow{DB_1}(0 < \lambda < 1) $, 则 (
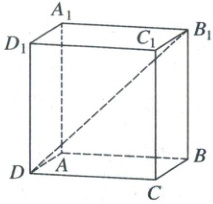
A.若 $ M $ 为 $ A_1D $ 的中点, 则三棱锥 $ P - BEM $ 体积为定值
B.存在点 $ P $ 使得 $ AP \perp BE $
C.当 $ \lambda = \frac{2}{3} $ 时, 平面 $ PBC $ 截长方体 $ ABCD - A_1B_1C_1D_1 $ 所得截面的面积为 $ \sqrt{5} $
D.若 $ Q $ 为长方体 $ ABCD - A_1B_1C_1D_1 $ 外接球上一点, $ \lambda = \frac{2}{3} $, 则 $ QE + 3QP $ 的最小值为 $ \sqrt{14} $
ACD
)
A.若 $ M $ 为 $ A_1D $ 的中点, 则三棱锥 $ P - BEM $ 体积为定值
B.存在点 $ P $ 使得 $ AP \perp BE $
C.当 $ \lambda = \frac{2}{3} $ 时, 平面 $ PBC $ 截长方体 $ ABCD - A_1B_1C_1D_1 $ 所得截面的面积为 $ \sqrt{5} $
D.若 $ Q $ 为长方体 $ ABCD - A_1B_1C_1D_1 $ 外接球上一点, $ \lambda = \frac{2}{3} $, 则 $ QE + 3QP $ 的最小值为 $ \sqrt{14} $
答案:
4.ACD【解析】长方体的结构特征+三棱锥的体积+空间中线面间的位置关系+空间向量的运算+阿氏球的性质
已知条件$\begin{cases} 线面平行的判定定理 \\ DB_1//平面BEM\rightarrow点P \\到平面BEM的距离为定值\rightarrow三棱锥的体积公式\end{cases}\rightarrow判断选项A$;
已知条件$\begin{cases} 反证法 \\ 假设AP\perp BE\rightarrow与正方形的性质产生矛盾\end{cases}\rightarrow判断选项B$;
已知条件$\begin{cases} 延长CP与A_1B_1交于G,取C_1D_1的中点F \\矩形BCFE为所得截面\rightarrow矩形的面积公式\end{cases}\rightarrow判断选项C$;
已知条件$\begin{cases} 阿氏球的性质\rightarrow3QP=QN,B_1N=DB_1 \\建系N,E点的坐标\rightarrow(QE+3QP)_{\min}=(QE+QN)_{\min}=NE\\两点间的距离公式\end{cases}\rightarrow判断选项D$.
对于A,因为$M$为$A_1D$的中点,$E$为$A_1B_1$的中点,所以$DB_1// EM$.因为$DB_1\not\subset平面BEM$,$EM\subset平面BEM$,所以$DB_1//平面BEM$(题眼).所以点$P$到平面$BEM$的距离为定值.因此三棱锥$P-BEM$的体积为定值.故A正确.对于B,假设存在点$P$使得$AP\perp BE$,又$AD\perp BE$,$AD\cap AP=A$,所以$BE\perp平面ADB_1$.又$AB_1\subset平面ADB_1$,所以$AB_1\perp BE$.因为四边形$ABB_1A_1$为正方形,所以$AB_1$与$BE$不垂直.产生矛盾,故不存在点$P$使得$AP\perp BE$,故B错误.对于C,延长$CP$与$A_1B_1$交于点$G$,由$CD// GB_1$,$\overrightarrow{DP}=\frac{2}{3}\overrightarrow{DB_1}$,得$\frac{GB_1}{CD}=\frac{1}{2}$,则$GB_1=1$,所以$G$是$A_1B_1$的中点,即点$G$与点$E$重合.取$C_1D_1$的中点$F$,则平面$PBC$截长方体$ABCD-A_1B_1C_1D_1$所得的截面为矩形$BCFE$,其面积为$\sqrt{5}$,故C正确.对于D,长方体$ABCD-A_1B_1C_1D_1$的外接球的球心为$B_1D$的中点,因为$\overrightarrow{DP}=\frac{2}{3}\overrightarrow{DB_1}$,由阿氏球得,在直线$B_1D$上必存在一点$N$,使得$3QP=QN$,此时点$N$在$DB_1$的延长线上,且满足$B_1N=DB_1$,以$D$为坐标原点,建立如图所示的空间直角坐标系.因为$DB_1=3$,$DN=6$,所以$\overrightarrow{DN}=2\overrightarrow{DB_1}$.所以$N(4,2,4)$.易得$E(1,1,2)$,所以$(QE+3QP)_{\min}=(QE+QN)_{\min}=NE=\sqrt{14}$(方法:两点间的距离公式求得).故D正确,故选ACD.
已知条件$\begin{cases} 线面平行的判定定理 \\ DB_1//平面BEM\rightarrow点P \\到平面BEM的距离为定值\rightarrow三棱锥的体积公式\end{cases}\rightarrow判断选项A$;
已知条件$\begin{cases} 反证法 \\ 假设AP\perp BE\rightarrow与正方形的性质产生矛盾\end{cases}\rightarrow判断选项B$;
已知条件$\begin{cases} 延长CP与A_1B_1交于G,取C_1D_1的中点F \\矩形BCFE为所得截面\rightarrow矩形的面积公式\end{cases}\rightarrow判断选项C$;
已知条件$\begin{cases} 阿氏球的性质\rightarrow3QP=QN,B_1N=DB_1 \\建系N,E点的坐标\rightarrow(QE+3QP)_{\min}=(QE+QN)_{\min}=NE\\两点间的距离公式\end{cases}\rightarrow判断选项D$.
对于A,因为$M$为$A_1D$的中点,$E$为$A_1B_1$的中点,所以$DB_1// EM$.因为$DB_1\not\subset平面BEM$,$EM\subset平面BEM$,所以$DB_1//平面BEM$(题眼).所以点$P$到平面$BEM$的距离为定值.因此三棱锥$P-BEM$的体积为定值.故A正确.对于B,假设存在点$P$使得$AP\perp BE$,又$AD\perp BE$,$AD\cap AP=A$,所以$BE\perp平面ADB_1$.又$AB_1\subset平面ADB_1$,所以$AB_1\perp BE$.因为四边形$ABB_1A_1$为正方形,所以$AB_1$与$BE$不垂直.产生矛盾,故不存在点$P$使得$AP\perp BE$,故B错误.对于C,延长$CP$与$A_1B_1$交于点$G$,由$CD// GB_1$,$\overrightarrow{DP}=\frac{2}{3}\overrightarrow{DB_1}$,得$\frac{GB_1}{CD}=\frac{1}{2}$,则$GB_1=1$,所以$G$是$A_1B_1$的中点,即点$G$与点$E$重合.取$C_1D_1$的中点$F$,则平面$PBC$截长方体$ABCD-A_1B_1C_1D_1$所得的截面为矩形$BCFE$,其面积为$\sqrt{5}$,故C正确.对于D,长方体$ABCD-A_1B_1C_1D_1$的外接球的球心为$B_1D$的中点,因为$\overrightarrow{DP}=\frac{2}{3}\overrightarrow{DB_1}$,由阿氏球得,在直线$B_1D$上必存在一点$N$,使得$3QP=QN$,此时点$N$在$DB_1$的延长线上,且满足$B_1N=DB_1$,以$D$为坐标原点,建立如图所示的空间直角坐标系.因为$DB_1=3$,$DN=6$,所以$\overrightarrow{DN}=2\overrightarrow{DB_1}$.所以$N(4,2,4)$.易得$E(1,1,2)$,所以$(QE+3QP)_{\min}=(QE+QN)_{\min}=NE=\sqrt{14}$(方法:两点间的距离公式求得).故D正确,故选ACD.
5. 在三棱柱 $ ABC - A_1B_1C_1 $ 中, $ \overrightarrow{AM} = 2\overrightarrow{MB}, \overrightarrow{A_1N} = m\overrightarrow{A_1C_1} $, 且 $ BN // $ 平面 $ A_1CM $, 则 $ m $ 的值为
$\frac{1}{2}$
_ 。
答案:
5.$\frac{1}{2}$ 空间向量的运算+共面向量 由题意知,$M,N$分别为棱$AB,A_1C_1$上的点,且$M$为靠近点$B$的一个三等分点,如图所示,则$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AB}$,所以$\overrightarrow{MA_1}=\overrightarrow{MA}+\overrightarrow{AA_1}=-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AA_1}$,$\overrightarrow{MC}=\overrightarrow{AC}-\overrightarrow{AM}=\overrightarrow{AC}-\frac{2}{3}\overrightarrow{AB}$.
因为$\overrightarrow{A_1N}=m\overrightarrow{A_1C_1}=m\overrightarrow{AC}$,所以$\overrightarrow{BN}=\overrightarrow{BA_1}+\overrightarrow{A_1N}=\overrightarrow{AA_1}-\overrightarrow{AB}+m\overrightarrow{AC}$(题眼)(提醒:在空间中选取基底向量时,注意三个向量为不共面向量).又$BN//平面A_1CM$,故$\overrightarrow{BN},\overrightarrow{MA_1},\overrightarrow{MC}$必共面(关键:由线面平行的性质推出向量共面),即存在$\lambda,\mu\in R$,使$\overrightarrow{BN}=\lambda\overrightarrow{MA_1}+\mu\overrightarrow{MC}$,即$\overrightarrow{AA_1}-\overrightarrow{AB}+m\overrightarrow{AC}=\lambda(-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AA_1})+\mu(\overrightarrow{AC}-\frac{2}{3}\overrightarrow{AB})=-\frac{2}{3}(\lambda+\mu)\overrightarrow{AB}+\lambda\overrightarrow{AA_1}+\mu\overrightarrow{AC}$,所以$\begin{cases}-\frac{2}{3}(\lambda+\mu)=-1,\\\mu=m,\\\lambda=1.\end{cases}$解得$m=\frac{1}{2}$.
因为$\overrightarrow{A_1N}=m\overrightarrow{A_1C_1}=m\overrightarrow{AC}$,所以$\overrightarrow{BN}=\overrightarrow{BA_1}+\overrightarrow{A_1N}=\overrightarrow{AA_1}-\overrightarrow{AB}+m\overrightarrow{AC}$(题眼)(提醒:在空间中选取基底向量时,注意三个向量为不共面向量).又$BN//平面A_1CM$,故$\overrightarrow{BN},\overrightarrow{MA_1},\overrightarrow{MC}$必共面(关键:由线面平行的性质推出向量共面),即存在$\lambda,\mu\in R$,使$\overrightarrow{BN}=\lambda\overrightarrow{MA_1}+\mu\overrightarrow{MC}$,即$\overrightarrow{AA_1}-\overrightarrow{AB}+m\overrightarrow{AC}=\lambda(-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AA_1})+\mu(\overrightarrow{AC}-\frac{2}{3}\overrightarrow{AB})=-\frac{2}{3}(\lambda+\mu)\overrightarrow{AB}+\lambda\overrightarrow{AA_1}+\mu\overrightarrow{AC}$,所以$\begin{cases}-\frac{2}{3}(\lambda+\mu)=-1,\\\mu=m,\\\lambda=1.\end{cases}$解得$m=\frac{1}{2}$.
6. 如图, 在底面为菱形的直四棱柱 $ ABCD - A_1B_1C_1D_1 $ 中, $ \angle BAD = \frac{2}{3}\pi, AA_1 = AB = 2 $, $ E, F, G $ 分别是 $ BB_1, CC_1, DD_1 $ 的中点.
(1) 求证: $ A_1E // GC $.
(2) 求平面 $ A_1EF $ 与平面 $ ABCD $ 所成角的大小.
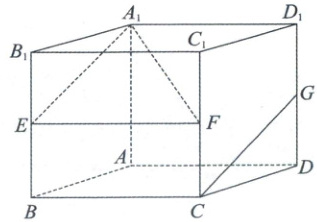
(1) 求证: $ A_1E // GC $.
(2) 求平面 $ A_1EF $ 与平面 $ ABCD $ 所成角的大小.

答案:
6.线线平行的判定+空间向量的应用
解:取$BC$中点$H$,连接$AH$.
∵底面$ABCD$为菱形,$\angle BAD=\frac{2}{3}\pi$,
$\therefore AH\perp AD$.
以$A$为坐标原点,$AH,AD,AA_1$所在直线分别为$x$轴、$y$轴、$z$轴建立如图所示的空间直角坐标系$A-xyz$,

则$A_1(0,0,2),E(\sqrt{3},-1,1),G(0,2,1),C(\sqrt{3},1,0),F(\sqrt{3},1,1)$.
(1)证明:由上述可得$\overrightarrow{A_1E}=(\sqrt{3},-1,-1),\overrightarrow{GC}=(\sqrt{3},-1,-1)$(题眼),
$\therefore\overrightarrow{A_1E}//\overrightarrow{GC}$.
$\therefore A_1E// GC$.
(2)设平面$A_1EF$的法向量为$\mathbf{n}=(x,y,z)$,
$\because\overrightarrow{EF}=(0,2,0)$,
则$\begin{cases}\mathbf{n}·\overrightarrow{A_1E}=0,\\\mathbf{n}·\overrightarrow{EF}=0,\end{cases}$即$\begin{cases}\sqrt{3}x-y-z=0,\\2y=0,\end{cases}$
取$x=1$,则$y=0,z=\sqrt{3}$,
$\therefore\mathbf{n}=(1,0,\sqrt{3})$(题眼).
易知$\overrightarrow{AA_1}=(0,0,2)$为平面$ABCD$的一个法向量,
设平面$A_1EF$与平面$ABCD$所成的角为$\theta$,
则$\cos\theta=\frac{|\overrightarrow{AA_1}·\mathbf{n}|}{|\overrightarrow{AA_1}|·|\mathbf{n}|}=\frac{2\sqrt{3}}{2×2}=\frac{\sqrt{3}}{2}$(提示:空间向量夹角公式),
$\therefore\theta=\frac{\pi}{6}$.
$\therefore$平面$A_1EF$与平面$ABCD$所成的角为$\frac{\pi}{6}$.
6.线线平行的判定+空间向量的应用
解:取$BC$中点$H$,连接$AH$.
∵底面$ABCD$为菱形,$\angle BAD=\frac{2}{3}\pi$,
$\therefore AH\perp AD$.
以$A$为坐标原点,$AH,AD,AA_1$所在直线分别为$x$轴、$y$轴、$z$轴建立如图所示的空间直角坐标系$A-xyz$,

则$A_1(0,0,2),E(\sqrt{3},-1,1),G(0,2,1),C(\sqrt{3},1,0),F(\sqrt{3},1,1)$.
(1)证明:由上述可得$\overrightarrow{A_1E}=(\sqrt{3},-1,-1),\overrightarrow{GC}=(\sqrt{3},-1,-1)$(题眼),
$\therefore\overrightarrow{A_1E}//\overrightarrow{GC}$.
$\therefore A_1E// GC$.
(2)设平面$A_1EF$的法向量为$\mathbf{n}=(x,y,z)$,
$\because\overrightarrow{EF}=(0,2,0)$,
则$\begin{cases}\mathbf{n}·\overrightarrow{A_1E}=0,\\\mathbf{n}·\overrightarrow{EF}=0,\end{cases}$即$\begin{cases}\sqrt{3}x-y-z=0,\\2y=0,\end{cases}$
取$x=1$,则$y=0,z=\sqrt{3}$,
$\therefore\mathbf{n}=(1,0,\sqrt{3})$(题眼).
易知$\overrightarrow{AA_1}=(0,0,2)$为平面$ABCD$的一个法向量,
设平面$A_1EF$与平面$ABCD$所成的角为$\theta$,
则$\cos\theta=\frac{|\overrightarrow{AA_1}·\mathbf{n}|}{|\overrightarrow{AA_1}|·|\mathbf{n}|}=\frac{2\sqrt{3}}{2×2}=\frac{\sqrt{3}}{2}$(提示:空间向量夹角公式),
$\therefore\theta=\frac{\pi}{6}$.
$\therefore$平面$A_1EF$与平面$ABCD$所成的角为$\frac{\pi}{6}$.
查看更多完整答案,请扫码查看


