《2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版》

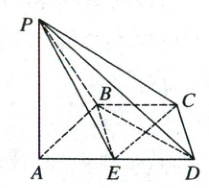
11. 如图, 在四棱雉 $ P - ABCD $ 中, $ AD // BC $, $ \angle ADC = \angle PAB = 90° $, $ AD = 2BC = 2CD = 4 $, $ E $ 为边 $ AD $ 的中点, $ PE \perp CD $.
(1) 求证: 平面 $ PAB \perp $ 平面 $ PBD $.
(2) 若直线 $ PD $ 与平面 $ ABCD $ 所成的角为 $ 45° $, 求点 $ A $ 到平面 $ PCE $ 的距离.

答案：
11.面面垂直的判定定理+空间中点到平面的距离
解：
(1)证明：因为$\angle ADC=90°$，所以$AD\perp CD$.
又因为$PE\perp CD$，$PE,ADC\subset平面PAD$，$PE\cap AD=E$，
所以$CD\perp平面PAD$.
因为$PAC\subset平面PAD$，所以$PA\perp CD$.
因为$PA\perp AB$，$AB,CDC\subset平面ABCD$，$AB,CD$相交，
所以$PA\perp平面ABCD$.
因为$BDC\subset平面ABCD$，所以$PA\perp BD$.
在四边形$ABCD$中，$AD// BC$，$\angle ADC=90°$，$AD=2BC=4$，
所以$BD=2\sqrt{2}$.
又因为$E$为边$AD$的中点，
所以$AE=DE=BC=2$.
又因为$AE// BC$，所以四边形$ABCE$为平行四边形.
所以$AB=CE=\sqrt{CD^2+DE^2}=2\sqrt{2}$.
所以$AD^2=AB^2+BD^2$.所以$AB\perp BD$.
又因为$PA\perp BD$，$PA,ABC\subset平面PAB$，$PA\cap AB=A$，
所以$BD\perp平面PAB$.
又因为$BDC\subset平面PBD$，所以平面$PAB\perp平面PBD$.
(2)延长$CB$至点$F$，使得$BF=CB=2$，连接$AF$，
因为$AD// BC$，$\angle ADC=90°$，$CF=AD=4$，
所以四边形$ADCF$为矩形.所以$AD\perp AF$.
由
(1)得$PA\perp平面ABCD$，
因为直线$PD$与平面$ABCD$所成的角为$45°$，
所以$\angle PDA=45°$.
因为$AD=4$，所以$PA=4$.
以$\overrightarrow{AD},\overrightarrow{AF},\overrightarrow{AP}$的方向分别为$x$轴、$y$轴、$z$轴的正方向建立如图所示的空间直角坐标系$A-xyz$，
　　　　
则$A(0,0,0),P(0,0,4),C(4,2,0),E(2,0,0)$，
则$\overrightarrow{PE}=(2,0,-4),\overrightarrow{EC}=(2,2,0)$.
设平面$PCE$的法向量为$\mathbf{n}=(x,y,z)$，
则$\begin{cases}\overrightarrow{PE}·\mathbf{n}=0,\\\mathbf{n}·\overrightarrow{EC}=0,\end{cases}$即$\begin{cases}2x-4z=0,\\2x+2y=0,\end{cases}$
取$x=2$，$y=-2$，$z=1$，
所以平面$PCE$的一个法向量$\mathbf{n}=(2,-2,1)$.
所以点$A$到平面$PCE$的距离$d=\frac{|\mathbf{n}·\overrightarrow{AP}|}{|\mathbf{n}|}=\frac{|0+0+4|}{\sqrt{4+4+1}}=\frac{4}{3}$.

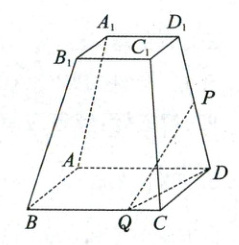
12. 如图, 已知四棱台 $ ABCD - A_1B_1C_1D_1 $ 的上、下底面分别是边长为 $ 2 $ 和 $ 4 $ 的正方形, 平面 $ AA_1D_1D \perp $ 平面 $ ABCD $, $ A_1A = D_1D = \sqrt{17} $, $ P $ 是棱 $ DD_1 $ 的中点, 点 $ Q $ 在棱 $ BC $ 上.
(1) 若 $ BQ = 3QC $, 证明: $ PQ // $ 平面 $ ABB_1A_1 $.
(2) 若二面角 $ P - QD - C $ 的正弦值为 $ \frac{5\sqrt{26}}{26} $, 求 $ BQ $ 的长.

答案：
12.线面平行的判定定理+线面垂直的判定定理与性质定理+二面角+空间向量的应用
思维导图
(2)已知条件$\begin{cases} 面面垂直的性质定理\rightarrow A_1O\perp平面ABCD \\建系\rightarrow得各点坐标\rightarrow相关向量\end{cases}$
解法一：设$\overrightarrow{CQ}=\lambda\overrightarrow{CB}(0\leqslant\lambda\leqslant1)\rightarrow平面向量的线性运算$
$\begin{cases} \overrightarrow{DQ}\rightarrow平面PDQ和平面DCQ的一个法向量 \\空间向量夹角公式\rightarrow得解\end{cases}$；
解法二：设点$Q(4,t,0)(-1\leqslant t\leqslant3)\rightarrow\overrightarrow{DQ}\rightarrow平面PDQ和平面DCQ的一个法向量\rightarrow空间向量夹角公式\rightarrow得解$；
解法三：作$PH\perp AD\rightarrow\begin{cases} 面面垂直的性质定理\rightarrow PH\perp DQ \\过点H作HG\perp DQ,垂足为G,连接PG\rightarrow\angle PGH是二面角P-QD-A的平面角\rightarrow解三角形\rightarrow得解.\end{cases}$
解：
(1)证明：如图1，取$AA_1$的中点$M$，连接$MP,MB$.
　　　　　　　
在四棱台$ABCD-A_1B_1C_1D_1$中，四边形$A_1ADD_1$是梯形，
$A_1D_1=2$，$AD=4$，
又$M,P$分别是棱$A_1A,D_1D$的中点，
所以$MP// AD$，且$MP=\frac{A_1D_1+AD}{2}=3$.
在正方形$ABCD$中，$BC// AD,BC=4$，
又$BQ=3QC$，所以$BQ=3$.
所以$MP\perp BQ$.
所以四边形$BMPQ$是平行四边形，
所以$PQ// MB$(提示：平行四边形的判定与性质).
又$MBC\subset平面ABB_1A_1$，$PQ\not\subset平面ABB_1A_1$，
所以$PQ//平面ABB_1A_1$(提示：线面平行的判定定理).
(2)在平面$AA_1D_1D$中，作$A_1O\perp AD$于点$O$.
因为平面$AA_1D_1D\perp平面ABCD$，平面$AA_1D_1D\cap平面ABCD=AD$，
$A_1O\perp AD$，$A_1OC\subset平面AA_1D_1D$，
所以$A_1O\perp平面ABCD$(提示：面面垂直的性质定理).
在正方形$ABCD$中，过点$O$作$AB$的平行线交$BC$于点$N$，则$ON\perp OD$.
以$ON,OD,OA_1$所在直线分别为$x$轴、$y$轴、$z$轴建立空间直角坐标系$O-xyz$，如图2所示.
　　　　　　　　
因为四边形$AA_1D_1D$是等腰梯形，$A_1D_1=2$，$AD=4$，
所以$AO=1$.
又$A_1A=D_1D=\sqrt{17}$，所以$A_1O=4$.
故$B(4,-1,0),D(0,3,0),C(4,3,0),D_1(0,2,4)$，
$P(0,\frac{5}{2},2)$，
所以$\overrightarrow{DC}=(4,0,0),\overrightarrow{DP}=(0,-\frac{1}{2},2),\overrightarrow{CB}=(0,-4,0)$.
解法一：设$\overrightarrow{CQ}=\lambda\overrightarrow{CB}=(0,-4\lambda,0)(0\leqslant\lambda\leqslant1)$(题眼)，
所以$\overrightarrow{DQ}=\overrightarrow{DC}+\overrightarrow{CQ}=(4,-4\lambda,0)$.
设平面$PDQ$的法向量为$\mathbf{m}=(x,y,z)$，
则$\begin{cases}\mathbf{m}·\overrightarrow{DP}=0,\\\mathbf{m}·\overrightarrow{DQ}=0,\end{cases}$即$\begin{cases}-\frac{1}{2}y+2z=0,\\4x-4\lambda y=0,\end{cases}$
取$z=1$，则$\mathbf{m}=(4\lambda,4,1)$.
易得平面$DCQ$的一个法向量为$\mathbf{n}=(0,0,1)$.
设二面角$P-QD-C$的平面角为$\theta$，
由题意得$|\cos\theta|=|\cos\langle\mathbf{m},\mathbf{n}\rangle|=\frac{|\mathbf{m}·\mathbf{n}|}{|\mathbf{m}|·|\mathbf{n}|}=\frac{1}{\sqrt{(4\lambda)^2+17}}=\frac{1}{\sqrt{26}}$(提示：空间向量夹角公式)，
所以$\frac{1}{\sqrt{(4\lambda)^2+17}}=\frac{1}{\sqrt{26}}$
解得$\lambda=\frac{3}{4}$(舍负)，
因此$CQ=\frac{3}{4}×4=3$，$BQ=1$，
所以当二面角$P-QD-C$的正弦值为$\frac{5\sqrt{26}}{26}$时，$BQ$的长为1.
解法二：设$Q(4,t,0)(-1\leqslant t\leqslant3)$，
所以$\overrightarrow{DQ}=(4,t-3,0)$(题眼).
设平面$PDQ$的法向量为$\mathbf{m}=(x,y,z)$，
则$\begin{cases}\mathbf{m}·\overrightarrow{DP}=0,\\\mathbf{m}·\overrightarrow{DQ}=0,\end{cases}$即$\begin{cases}-\frac{1}{2}y+2z=0,\\4x+(t-3)y=0,\end{cases}$
取$y=4$，则$\mathbf{m}=(3-t,4,1)$，
易得平面$DCQ$的一个法向量为$\mathbf{n}=(0,0,1)$.
设二面角$P-QD-C$的平面角为$\theta$，
由题意得$|\cos\theta|=|\cos\langle\mathbf{m},\mathbf{n}\rangle|=\frac{|\mathbf{m}·\mathbf{n}|}{|\mathbf{m}|·|\mathbf{n}|}=\frac{1}{\sqrt{(3-t)^2+17}}=\frac{1}{\sqrt{26}}$(提示：空间向量夹角公式)，
解得$t=0$或$t=6$(舍)，因此$BQ=1$，
所以当二面角$P-QD-C$的正弦值为$\frac{5\sqrt{26}}{26}$时，$BQ$的长为1.
解法三：在平面$A_1ADD_1$中，作$PH\perp AD$，垂足为$H$，
如图3.

因为平面$A_1ADD_1\perp平面ABCD$，
平面$A_1ADD_1\cap平面ABCD=AD$，$PHC\subset平面A_1ADD_1$，
所以$PH\perp平面ABCD$(提示：面面垂直的性质定理).
又$DQC\subset平面ABCD$，
所以$PH\perp DQ$.
在平面$ABCD$中，过点$H$作$HG\perp DQ$，垂足为$G$，连接$PG$.
因为$PH\perp DQ$，$HG\perp DQ$，$PH\cap HG=H$，$PH,HGC\subset平面PHG$，
所以$DQ\perp平面PHG$.
又$PGC\subset平面PHG$，
所以$DQ\perp PG$(提示：线面垂直的性质定理).
因为$\angle PGH$是二面角$P-QD-A$的平面角(题眼).
在四棱台$ABCD-A_1B_1C_1D_1$中，四边形$A_1ADD_1$是梯形，
$A_1D_1=2$，$AD=4$，$A_1A=D_1D=\sqrt{17}$，$P$是棱$DD_1$的中点，
所以$PH=2$，$DH=\frac{1}{2}$.
设$BQ=x(0\leqslant x\leqslant4)$，则$CQ=4-x$，$DQ=\sqrt{4^2+(4-x)^2}=\sqrt{x^2-8x+32}$，
在$\triangle QHD$中，$\frac{1}{2}×\frac{1}{2}×4=\frac{1}{2}×\sqrt{x^2-8x+32}· HG$(提示：等面积法)，
解得$HG=\frac{2}{\sqrt{x^2-8x+32}}$，
因为二面角$P-QD-C$的平面角与二面角$P-QD-A$的平面角互补，
且二面角$P-QD-C$的正弦值为$\frac{5\sqrt{26}}{26}$，
所以$\sin\angle PGH=\frac{5\sqrt{26}}{26}$.
所以$\tan\angle PGH=5$.
所以在$Rt\triangle PHG$中，$\frac{PH}{HG}=\sqrt{x^2-8x+32}=5$.
解得$x=1$或$x=7$(舍).
所以当二面角$P-QD-C$的正弦值为$\frac{5\sqrt{26}}{26}$时，$BQ$的长为1.