2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天利38套对接高考单元专题测试卷高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. (13分) 正方体 $ABCD - A_1B_1C_1D_1$ 中,$E,F$ 分别是 $BB_1,CD$ 的中点.
(1) 求证:平面 $AED\perp$ 平面 $A_1FD_1$.
(2) 在 $AE$ 上求一点 $M$,使得 $A_1M\perp$ 平面 $DAE$.
(1) 求证:平面 $AED\perp$ 平面 $A_1FD_1$.
(2) 在 $AE$ 上求一点 $M$,使得 $A_1M\perp$ 平面 $DAE$.
答案:
15.空间法向量的应用+空间中直线与平面的位置关系
解:
(1)证明:建立如图所示的空间直角坐标系$D-xyz$,
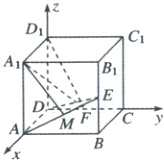
不妨设正方体的棱长为$2$,则$A(2,0,0)$,$E(2,2,1)$,$F(0,1,0)$,$A_{1}(2,0,2)$,$D_{1}(0,0,2)$.设平面$AED$的法向量为$\boldsymbol{n_{1}}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{n_{1}}·\overrightarrow{DA}=(x_{1},y_{1},z_{1})·(2,0,0)=0,\\\boldsymbol{n_{1}}·\overrightarrow{DE}=(x_{1},y_{1},z_{1})·(2,2,1)=0.\end{cases}$则$\begin{cases}2x_{1}=0,\\2x_{1}+2y_{1}+z_{1}=0.\end{cases}$令$y_{1}=1$,得$\boldsymbol{n_{1}}=(0,1,-2)$.同理可得平面$A_{1}FD_{1}$的一个法向量$\boldsymbol{n_{2}}=(0,2,1)$.$\because\boldsymbol{n_{1}}·\boldsymbol{n_{2}}=0$,$\therefore$平面$AED\perp$平面$A_{1}FD_{1}$.(6分)
(2)由于点$M$在$AE$上,$\therefore$可设$\overrightarrow{AM}=\lambda\overrightarrow{AE}=\lambda(0,2,1)=(0,2\lambda,\lambda)(\lambda\in\mathbf{R})$.可得$M(2,2\lambda,\lambda)$,于是$\overrightarrow{A_{1}M}=(0,2\lambda,\lambda-2)$.要使$\overrightarrow{A_{1}M}\perp$平面$DAE$,需$\overrightarrow{A_{1}M}·\overrightarrow{AE}=0$,即$\overrightarrow{A_{1}M}·\overrightarrow{AE}=(0,2\lambda,\lambda-2)·(0,2,1)=5\lambda-2=0$,得$\lambda=\frac{2}{5}$.故当$AM=\frac{2}{5}AE$,即点$M$坐标为$(2,\frac{4}{5},\frac{2}{5})$时,$\overrightarrow{A_{1}M}\perp$平面$DAE$.(13分)
15.空间法向量的应用+空间中直线与平面的位置关系
解:
(1)证明:建立如图所示的空间直角坐标系$D-xyz$,

不妨设正方体的棱长为$2$,则$A(2,0,0)$,$E(2,2,1)$,$F(0,1,0)$,$A_{1}(2,0,2)$,$D_{1}(0,0,2)$.设平面$AED$的法向量为$\boldsymbol{n_{1}}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\boldsymbol{n_{1}}·\overrightarrow{DA}=(x_{1},y_{1},z_{1})·(2,0,0)=0,\\\boldsymbol{n_{1}}·\overrightarrow{DE}=(x_{1},y_{1},z_{1})·(2,2,1)=0.\end{cases}$则$\begin{cases}2x_{1}=0,\\2x_{1}+2y_{1}+z_{1}=0.\end{cases}$令$y_{1}=1$,得$\boldsymbol{n_{1}}=(0,1,-2)$.同理可得平面$A_{1}FD_{1}$的一个法向量$\boldsymbol{n_{2}}=(0,2,1)$.$\because\boldsymbol{n_{1}}·\boldsymbol{n_{2}}=0$,$\therefore$平面$AED\perp$平面$A_{1}FD_{1}$.(6分)
(2)由于点$M$在$AE$上,$\therefore$可设$\overrightarrow{AM}=\lambda\overrightarrow{AE}=\lambda(0,2,1)=(0,2\lambda,\lambda)(\lambda\in\mathbf{R})$.可得$M(2,2\lambda,\lambda)$,于是$\overrightarrow{A_{1}M}=(0,2\lambda,\lambda-2)$.要使$\overrightarrow{A_{1}M}\perp$平面$DAE$,需$\overrightarrow{A_{1}M}·\overrightarrow{AE}=0$,即$\overrightarrow{A_{1}M}·\overrightarrow{AE}=(0,2\lambda,\lambda-2)·(0,2,1)=5\lambda-2=0$,得$\lambda=\frac{2}{5}$.故当$AM=\frac{2}{5}AE$,即点$M$坐标为$(2,\frac{4}{5},\frac{2}{5})$时,$\overrightarrow{A_{1}M}\perp$平面$DAE$.(13分)
16. (15分) 如图所示,$PD$ 垂直于正方形 $ABCD$ 所在的平面,$AB = 2$,点 $E$ 是 $PB$ 的中点,且 $AE$ 与 $PD$ 所成角的余弦值为 $\frac{\sqrt{3}}{3}$.
(1) 求 $PD$ 的长.
(2) 在 $AD$ 上是否存在一点 $F$,使 $EF\perp$ 平面 $PBC$?若存在,确定其位置;若不存在,请说明理由.
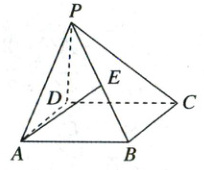
(1) 求 $PD$ 的长.
(2) 在 $AD$ 上是否存在一点 $F$,使 $EF\perp$ 平面 $PBC$?若存在,确定其位置;若不存在,请说明理由.

答案:
16.空间向量的应用+空间中直线与平面的位置关系
解:以$D$为坐标原点,建立如图所示的空间直角坐标系,(1分)
设$PD$的长为$z(z>0)$,
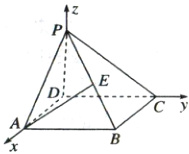
则$B(2,2,0)$,$P(0,0,z)$,$A(2,0,0)$,$C(0,2,0)$,所以$E(1,1,\frac{z}{2})$.
(1)$\overrightarrow{AE}=(-1,1,\frac{z}{2})$,$\overrightarrow{DP}=(0,0,z)$.因为$\frac{\overrightarrow{AE}·\overrightarrow{DP}}{|\overrightarrow{AE}||\overrightarrow{DP}|}=\frac{\sqrt{3}}{3}$,所以$\frac{\frac{z^{2}}{2}}{\sqrt{1+1+\frac{z^{2}}{4}}·\sqrt{z^{2}}}=\frac{\sqrt{3}}{3}$.解得$z=2$,即$PD$的长为$2$.(7分)
(2)存在,$F$为$AD$的中点.(8分)假设在$AD$上存在一点$F$,使$EF\perp$平面$PBC$,设$F(a,0,0)$,其中$0<a<2$,则$\overrightarrow{EF}=(a-1,-1,-1)$,$\overrightarrow{BC}=(-2,0,0)$,$\overrightarrow{PB}=(2,2,-2)$.因为$\overrightarrow{EF}\perp$平面$PBC$,所以$\overrightarrow{EF}·\overrightarrow{BC}=0$且$\overrightarrow{EF}·\overrightarrow{PB}=0$.即$-2(a-1)=0$且$2(a-1)-2+2=0$,所以$a=1$.所以存在点$F$使$\overrightarrow{EF}\perp$平面$PBC$,且$F$为$AD$的中点.(15分)
16.空间向量的应用+空间中直线与平面的位置关系
解:以$D$为坐标原点,建立如图所示的空间直角坐标系,(1分)
设$PD$的长为$z(z>0)$,

则$B(2,2,0)$,$P(0,0,z)$,$A(2,0,0)$,$C(0,2,0)$,所以$E(1,1,\frac{z}{2})$.
(1)$\overrightarrow{AE}=(-1,1,\frac{z}{2})$,$\overrightarrow{DP}=(0,0,z)$.因为$\frac{\overrightarrow{AE}·\overrightarrow{DP}}{|\overrightarrow{AE}||\overrightarrow{DP}|}=\frac{\sqrt{3}}{3}$,所以$\frac{\frac{z^{2}}{2}}{\sqrt{1+1+\frac{z^{2}}{4}}·\sqrt{z^{2}}}=\frac{\sqrt{3}}{3}$.解得$z=2$,即$PD$的长为$2$.(7分)
(2)存在,$F$为$AD$的中点.(8分)假设在$AD$上存在一点$F$,使$EF\perp$平面$PBC$,设$F(a,0,0)$,其中$0<a<2$,则$\overrightarrow{EF}=(a-1,-1,-1)$,$\overrightarrow{BC}=(-2,0,0)$,$\overrightarrow{PB}=(2,2,-2)$.因为$\overrightarrow{EF}\perp$平面$PBC$,所以$\overrightarrow{EF}·\overrightarrow{BC}=0$且$\overrightarrow{EF}·\overrightarrow{PB}=0$.即$-2(a-1)=0$且$2(a-1)-2+2=0$,所以$a=1$.所以存在点$F$使$\overrightarrow{EF}\perp$平面$PBC$,且$F$为$AD$的中点.(15分)
17. (15分) 如图,在四棱柱 $ABCD - A_1B_1C_1D_1$ 中,侧面 $ABB_1A_1$ 是正方形,平面 $ABB_1A_1\perp$ 平面 $ABCD$,$AB// CD$,$AD = DC = \frac{1}{2}AB$,$M$ 为线段 $AB$ 的中点,$AD\perp B_1M$.
(1) 求证:$C_1M//$ 平面 $ADD_1A_1$.
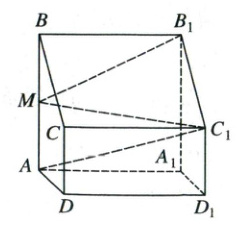
(2) 求直线 $AC_1$ 与平面 $MB_1C_1$ 所成角的正弦值.
(1) 求证:$C_1M//$ 平面 $ADD_1A_1$.

(2) 求直线 $AC_1$ 与平面 $MB_1C_1$ 所成角的正弦值.
答案:
17.线面平行的判定定理+直线与平面成角的正弦值
解:
(1)证明:如图1,连接$AD_{1},$
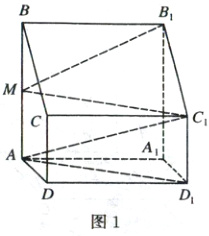
在四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$中,侧面$CDD_{1}C_{1}$为平行四边形,所以$C_{1}D_{1}// CD,$$C_{1}D_{1}=CD.$因为AB// CD,$CD=\frac{1}{2}AB,$M为AB的中点,所以CD// AM,CD=AM.所以$C_{1}D_{1}// AM,$且$C_{1}D_{1}=AM.$所以四边形$MAD_{1}C_{1}$为平行四边形.所以$C_{1}M// AD_{1}($题眼).因为$C_{1}M\not\subset$平面$ADD_{1}A_{1},$$AD_{1}\subset$平面$ADD_{1}A_{1},$所以$C_{1}M//$平面$ADD_{1}A_{1}($提示:线面平行的判定定理).(5分)
(2)在正方形$ABB_{1}A_{1}$中,$AA_{1}\perp AB.$因为平面$ABB_{1}A_{1}\perp$平面ABCD,平面$ABB_{1}A_{1}\cap$平面ABCD=AB,$AA_{1}\subset$平面$ABB_{1}A_{1},$所以$AA_{1}\perp$平面ABCD(提示:平面与平面垂直的性质定理).又$AD\subset$平面ABCD,所以$AA_{1}\perp AD.$因为$AD\perp B_{1}M,$$AA_{1},B_{1}M\subset$平面$ABB_{1}A_{1},$且$B_{1}M$与$AA_{1}$相交,所以$AD\perp$平面$ABB_{1}A_{1}.$又$ABC\subset$平面$ABB_{1}A_{1},$所以$AD\perp AB($提示:利用直线与平面垂直的判定定理证明直线垂直平面,再利用直线与平面垂直的性质定理得到直线与直线垂直).如图2,以A为坐标原点,$AD,AA_{1},AB$所在直线分别为x,y,z轴建立空间直角坐标系A-xyz.

不妨设AD=1,则A(0,0,0),$C_{1}(1,2,1),$$B_{1}(0,2,2),$M(0,0,1)(题眼),所以$\overrightarrow{AC_{1}}=(1,2,1),$$\overrightarrow{C_{1}B_{1}}=(-1,0,1),$$\overrightarrow{MC_{1}}=(1,2,0).$设平面$MB_{1}C_{1}$的法向量为$\boldsymbol{n}=(x,y,z),$则$\begin{cases}\boldsymbol{n}·\overrightarrow{C_{1}B_{1}}=0,\\\boldsymbol{n}·\overrightarrow{MC_{1}}=0,\end{cases}$即$\begin{cases}-x+z=0,\\x+2y=0.\end{cases}$令x=2,则y=-1,z=2,于是$\boldsymbol{n}=(2,-1,2).$因为$\cos\langle\overrightarrow{AC_{1}},\boldsymbol{n}\rangle=\frac{\overrightarrow{AC_{1}}·\boldsymbol{n}}{|\overrightarrow{AC_{1}}|·|\boldsymbol{n}|}=\frac{\sqrt{6}}{9}$,
17.线面平行的判定定理+直线与平面成角的正弦值
解:
(1)证明:如图1,连接$AD_{1},$

在四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$中,侧面$CDD_{1}C_{1}$为平行四边形,所以$C_{1}D_{1}// CD,$$C_{1}D_{1}=CD.$因为AB// CD,$CD=\frac{1}{2}AB,$M为AB的中点,所以CD// AM,CD=AM.所以$C_{1}D_{1}// AM,$且$C_{1}D_{1}=AM.$所以四边形$MAD_{1}C_{1}$为平行四边形.所以$C_{1}M// AD_{1}($题眼).因为$C_{1}M\not\subset$平面$ADD_{1}A_{1},$$AD_{1}\subset$平面$ADD_{1}A_{1},$所以$C_{1}M//$平面$ADD_{1}A_{1}($提示:线面平行的判定定理).(5分)
(2)在正方形$ABB_{1}A_{1}$中,$AA_{1}\perp AB.$因为平面$ABB_{1}A_{1}\perp$平面ABCD,平面$ABB_{1}A_{1}\cap$平面ABCD=AB,$AA_{1}\subset$平面$ABB_{1}A_{1},$所以$AA_{1}\perp$平面ABCD(提示:平面与平面垂直的性质定理).又$AD\subset$平面ABCD,所以$AA_{1}\perp AD.$因为$AD\perp B_{1}M,$$AA_{1},B_{1}M\subset$平面$ABB_{1}A_{1},$且$B_{1}M$与$AA_{1}$相交,所以$AD\perp$平面$ABB_{1}A_{1}.$又$ABC\subset$平面$ABB_{1}A_{1},$所以$AD\perp AB($提示:利用直线与平面垂直的判定定理证明直线垂直平面,再利用直线与平面垂直的性质定理得到直线与直线垂直).如图2,以A为坐标原点,$AD,AA_{1},AB$所在直线分别为x,y,z轴建立空间直角坐标系A-xyz.

不妨设AD=1,则A(0,0,0),$C_{1}(1,2,1),$$B_{1}(0,2,2),$M(0,0,1)(题眼),所以$\overrightarrow{AC_{1}}=(1,2,1),$$\overrightarrow{C_{1}B_{1}}=(-1,0,1),$$\overrightarrow{MC_{1}}=(1,2,0).$设平面$MB_{1}C_{1}$的法向量为$\boldsymbol{n}=(x,y,z),$则$\begin{cases}\boldsymbol{n}·\overrightarrow{C_{1}B_{1}}=0,\\\boldsymbol{n}·\overrightarrow{MC_{1}}=0,\end{cases}$即$\begin{cases}-x+z=0,\\x+2y=0.\end{cases}$令x=2,则y=-1,z=2,于是$\boldsymbol{n}=(2,-1,2).$因为$\cos\langle\overrightarrow{AC_{1}},\boldsymbol{n}\rangle=\frac{\overrightarrow{AC_{1}}·\boldsymbol{n}}{|\overrightarrow{AC_{1}}|·|\boldsymbol{n}|}=\frac{\sqrt{6}}{9}$,
所以直线$AC_{1}$与平面$MB_{1}C_{1}$所成角的正弦值为$\frac{\sqrt{6}}{9}$。
(15分)
查看更多完整答案,请扫码查看


