2025年新课程学习与检测八年级物理上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测八年级物理上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
阅读材料,完成第1~5题。
汽车前后保险杠内安装有多个超声波雷达传感器,用于测量汽车与前后左右各个物体间的距离,如图2所示。图3为超声波测量仪器的模拟实验装置图,模拟实验装置的使用说明书如下:
|使用说明书|
|----|
|(1)实验装置如图3所示,甲、乙是声信号采集器。|
|(2)用棒槌敲打铜铃,声音被甲、乙接收。|
|(3)液晶显示屏显示甲、乙接收到声信号的时间差,单位为毫秒(1毫秒=0.001秒)。|
1. 如图1所示,汽车外部的后视镜是
2. 汽车雷达启动后发出
3. 若把铜铃放在甲、乙的中点,则液晶显示屏的示数为
4. 若把铜铃放在乙的右边,以恒定的速度向右不断远离乙,则液晶显示屏的数值将
5. 如图3所示,s₁=0.36m,s₂=1.22m,液晶显示屏上显示:2.50,则此时声速为


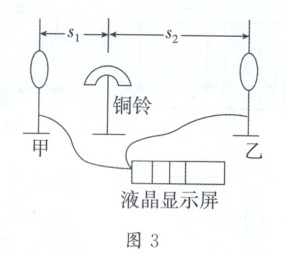
汽车前后保险杠内安装有多个超声波雷达传感器,用于测量汽车与前后左右各个物体间的距离,如图2所示。图3为超声波测量仪器的模拟实验装置图,模拟实验装置的使用说明书如下:
|使用说明书|
|----|
|(1)实验装置如图3所示,甲、乙是声信号采集器。|
|(2)用棒槌敲打铜铃,声音被甲、乙接收。|
|(3)液晶显示屏显示甲、乙接收到声信号的时间差,单位为毫秒(1毫秒=0.001秒)。|
1. 如图1所示,汽车外部的后视镜是
凸面
镜,能起到扩大司机视野的作用。2. 汽车雷达启动后发出
超声波
用于测量物体间的距离,激光
能用于太空测距。(均选填“超声波”“次声波”或“激光”)3. 若把铜铃放在甲、乙的中点,则液晶显示屏的示数为
0
。4. 若把铜铃放在乙的右边,以恒定的速度向右不断远离乙,则液晶显示屏的数值将
不变
(选填“变大”“变小”或“不变”)。5. 如图3所示,s₁=0.36m,s₂=1.22m,液晶显示屏上显示:2.50,则此时声速为
344
m/s。


答案:
1.凸面 解析:如图1所示,汽车外部的后视镜是凸面镜,能起到扩大司机视野的用途。
2.超声波 激光 解析:汽车雷达启动后发出超声波用于测量物体间的距离,声音的传播需要介质,真空不能传声,月球周围和太空没有空气,是真空,故超声波和次声波不能用于太空测距,但是光的传播不需要介质,故激光可以用于太空测距。
3.0 解析:如果铜铃在甲、乙中点,由于声速相同,声音传递到甲、乙的时间相等,故此时液晶显示屏的示数为0。
4.不变 解析:声音从铜铃到甲的时间$t_{甲}=\frac{s_{1}}{v_{声}}$,声音从铜铃到乙的时间$t_{乙}=\frac{s_{2}}{v_{声}}$,若把铜铃放在乙的右边,以恒定的速度向右不断远离乙,声音到达甲、乙的时间差为
$\Delta t=t_{甲}-t_{乙}=\frac{s_{1}}{v_{声}}-\frac{s_{2}}{v_{声}}=\frac{s_{1}-s_{2}}{v_{声}}$,
因为铜铃与甲、乙在一条直线上,且由于乙与甲的距离是一定的,所以声音传到乙和甲的时间差是不变的。
5.344 解析:由4题可知$\Delta t=\frac{\vert s_{1}-s_{2}\vert}{v_{声}}$,当时间差$\Delta t=2.5ms=2.5 × 10^{-3}s$,声速为
$v_{声}=\frac{\vert s_{1}-s_{2}\vert}{\Delta t}=\frac{1.22m - 0.36m}{2.5 × 10^{-3}s}=344m/s$。
2.超声波 激光 解析:汽车雷达启动后发出超声波用于测量物体间的距离,声音的传播需要介质,真空不能传声,月球周围和太空没有空气,是真空,故超声波和次声波不能用于太空测距,但是光的传播不需要介质,故激光可以用于太空测距。
3.0 解析:如果铜铃在甲、乙中点,由于声速相同,声音传递到甲、乙的时间相等,故此时液晶显示屏的示数为0。
4.不变 解析:声音从铜铃到甲的时间$t_{甲}=\frac{s_{1}}{v_{声}}$,声音从铜铃到乙的时间$t_{乙}=\frac{s_{2}}{v_{声}}$,若把铜铃放在乙的右边,以恒定的速度向右不断远离乙,声音到达甲、乙的时间差为
$\Delta t=t_{甲}-t_{乙}=\frac{s_{1}}{v_{声}}-\frac{s_{2}}{v_{声}}=\frac{s_{1}-s_{2}}{v_{声}}$,
因为铜铃与甲、乙在一条直线上,且由于乙与甲的距离是一定的,所以声音传到乙和甲的时间差是不变的。
5.344 解析:由4题可知$\Delta t=\frac{\vert s_{1}-s_{2}\vert}{v_{声}}$,当时间差$\Delta t=2.5ms=2.5 × 10^{-3}s$,声速为
$v_{声}=\frac{\vert s_{1}-s_{2}\vert}{\Delta t}=\frac{1.22m - 0.36m}{2.5 × 10^{-3}s}=344m/s$。
查看更多完整答案,请扫码查看


