15. 如图 2 - 6 所示,刻度尺的分度值是
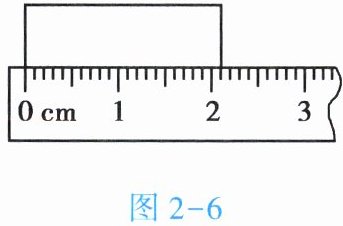
1mm
,所测物体的长度是2.10
cm。
答案:
1mm
2.10
2.10
16. 为了探究小球自由下落时的运动,某物理实验小组的同学用照相机每隔相等的时间自动拍照一次,拍下小球下落时的运动状态,如图 2 - 7 所示。可以看出小球在做

变速
(填“匀速”或“变速”)直线运动,理由是在相同的时间内通过的路程不相等
。
答案:
变速
在相同的时间内通过的路程不相等
在相同的时间内通过的路程不相等
17. 有一段用固定镜头拍摄的一列武广高铁动车组视频,小田通过播放该视频来测算机车运行速度。已知机车长度是 s,测算的步骤如下,请将步骤 C 补充完整,并排列测算步骤的合理顺序:
A.记下机车头到达观测点的时刻;
B.计算整列车通过观测点所用的时间 t;
C.在画面上选择一个______;
D.利用 $ v = \frac{s}{t} $ 计算出机车运行的速度;
E.记下机车尾到达观测点的时刻。
CAEBD
(填字母)。A.记下机车头到达观测点的时刻;
B.计算整列车通过观测点所用的时间 t;
C.在画面上选择一个______;
D.利用 $ v = \frac{s}{t} $ 计算出机车运行的速度;
E.记下机车尾到达观测点的时刻。
答案:
CAEBD
观测点
观测点
18. 运动会进行 100 m 决赛时,同学们测量了运动员到达距离起点 20 m、80 m、100 m 时各自所用的时间。其中三名同学的时间如下表所示。
| | 到达 20 m 处所用时间/s | 到达 80 m 处所用时间/s | 到达 100 m 处所用时间/s |
| 王小兵 | 2.3 | 8.9 | 12.2 |
| 刘磊 | 2.4 | 8.3 | 11.8 |
| 周伟 | 2.5 | 8.4 | 11.4 |
算出这三位同学分别在 0~20 m、20~80 m、80~100 m 区间内的平均速度,设计表格将计算结果填入其中(要求有计算过程)。
| | 到达 20 m 处所用时间/s | 到达 80 m 处所用时间/s | 到达 100 m 处所用时间/s |
| 王小兵 | 2.3 | 8.9 | 12.2 |
| 刘磊 | 2.4 | 8.3 | 11.8 |
| 周伟 | 2.5 | 8.4 | 11.4 |
算出这三位同学分别在 0~20 m、20~80 m、80~100 m 区间内的平均速度,设计表格将计算结果填入其中(要求有计算过程)。
答案:
解:根据表中数据可知,王小兵在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.3\ \mathrm {s}、$$8.9\ \mathrm {s} $和$12.2\ \mathrm {s},$则王小兵在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.3\ \mathrm {s}}≈8.7\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.9\ \mathrm {s}-2.3\ \mathrm {s}}≈9.1\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{12.2\ \mathrm {s}-8.9}≈6.1\ \mathrm {m/s};$
根据表中数据可知,刘磊在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.4\ \mathrm {s}、$$8.3\ \mathrm {s} $和$11.8\ \mathrm {s},$则刘磊在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.4\ \mathrm {s}}≈8.3\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.3\ \mathrm {s}-2.4\ \mathrm {s}}≈10.2\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{11.8\ \mathrm {s}-8.3\ \mathrm {s}}≈5.7\ \mathrm {m/s};$
根据表中数据可知,周伟在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.5\ \mathrm {s}、$$8.4\ \mathrm {s} $和$11.4\ \mathrm {s},$则周伟在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.5\ \mathrm {s}}≈8.0\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.4\ \mathrm {s}-2.5\ \mathrm {s}}≈10.2\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{11.4\ \mathrm {s}-8.4\ \mathrm {s}}≈6.7\ \mathrm {m/s};$
设计表格并填入数据,如下表所示:
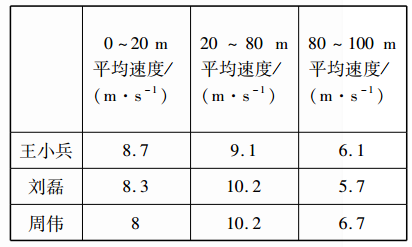
解:根据表中数据可知,王小兵在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.3\ \mathrm {s}、$$8.9\ \mathrm {s} $和$12.2\ \mathrm {s},$则王小兵在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.3\ \mathrm {s}}≈8.7\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.9\ \mathrm {s}-2.3\ \mathrm {s}}≈9.1\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{12.2\ \mathrm {s}-8.9}≈6.1\ \mathrm {m/s};$
根据表中数据可知,刘磊在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.4\ \mathrm {s}、$$8.3\ \mathrm {s} $和$11.8\ \mathrm {s},$则刘磊在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.4\ \mathrm {s}}≈8.3\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.3\ \mathrm {s}-2.4\ \mathrm {s}}≈10.2\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{11.8\ \mathrm {s}-8.3\ \mathrm {s}}≈5.7\ \mathrm {m/s};$
根据表中数据可知,周伟在$0~20\ \mathrm {m}、$$20~80\ \mathrm {m}、$$80~100\ \mathrm {m} $所用的时间分别为$2.5\ \mathrm {s}、$$8.4\ \mathrm {s} $和$11.4\ \mathrm {s},$则周伟在不同路段的平均速度:
$v_{1}=\frac {s_{1}}{t_{1}}=\frac {20\ \mathrm {m}}{2.5\ \mathrm {s}}≈8.0\ \mathrm {m/s};$
$v_{2}=\frac {s_{2}}{t_{2}}=\frac {80\ \mathrm {m}-20\ \mathrm {m}}{8.4\ \mathrm {s}-2.5\ \mathrm {s}}≈10.2\ \mathrm {m/s};$
$v_{3}=\frac {s_{3}}{t_{3}}=\frac {100\ \mathrm {m}-80\ \mathrm {m}}{11.4\ \mathrm {s}-8.4\ \mathrm {s}}≈6.7\ \mathrm {m/s};$
设计表格并填入数据,如下表所示:

查看更多完整答案,请扫码查看


