《2025年学生基础性作业四年级数学上册北师大版》

1. $38 + 246 = 246 + 38$,运用了(加法交换律)。

答案： 加法交换律

2. 运用加法交换律和乘法交换律填空。
$35×28 = 28×$(35) $88 + 126 = 126 +$(88)
$47×$(21)$= 21×$(47) $159 + 53 =$(53)$+$(159)
$a + b =$(b)$+$(a) $a×b =$(b)$×$(a)

答案： $35$；$88$；$21$，$47$；$53$，$159$；$b$，$a$；$b$，$a$。

3. 不笔算,在$◯$里填上“$＞$”“$＜$”或“$=$”。
$45 + 54◯$=$54 + 45$ $24×76◯$＞$67×24$ $22 + 260◯$＜$260×22$

答案： =；＞；＜

二、用竖式计算,并运用加法交换律或乘法交换律验算。
$78 + 327 = $405 $658 + 203 = $861
$74×29 = $2146 $109×44 = $4796

答案： 78 + 327 = 405
658 + 203 = 861
74×29 = 2146
109×44=4796

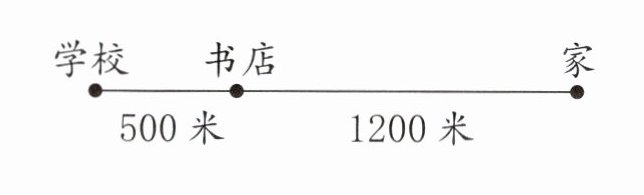
三、结合下图,说明等式为什么成立？
$500 + 1200 = 1200 + 500$

答案： 由图可知，从学校到书店距离 500 米，从书店到家距离 1200 米，那么学校到家的距离有两种计算方式：
从学校到书店再到家，先算学校到书店距离加书店到家距离，即$500 + 1200$；
把学校到书店和书店到家的方向调换，先算书店到家距离加学校到书店距离，即$1200 + 500$，它们都表示学校到家的距离。
所以$500 + 1200 = 1200 + 500$，根据加法交换律，两个数相加，交换加数的位置，和不变。
故等式成立。