1. 甲数是$x$,乙数比甲数的2倍少8,乙数是( )。
答案:
2x-8
2. 如右图所示,把两个完全相同的三角形拼成一个平行四边形,平行四边形的底是$a$,高是$h$,面积是( ),每个三角形的面积是( )。
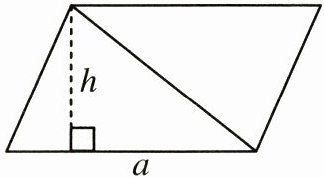

答案:
ah $\frac{1}{2}ah$
3. 一辆公共汽车上原来有35人,到新街站下去$x$人,又上来$y$人,现在有( )人。
答案:
35-x+y
4. 红光小学买来8个篮球和6个足球,每个篮球$a$元,每个足球$b$元,花了( )元,当$a = 55$,$b = 65$时,应付( )元。
答案:
8a+6b 830
5. 若$x - 9 = 11$,则$4x + 2 = $( );若$2x + y + 6 = 12$,则$4x + 2y = $( )。
答案:
82 12
6. $0.85公顷= $( )平方米 $9.28\ m^{2}= $( )$dm^{2}$
答案:
8500 928
7. (1)已知一个平行四边形的底是$6\ cm$,高是$4.2\ cm$,则面积是( )$cm^{2}$。
(2)若平行四边形的底是$9.8\ dm$,面积是$117.6\ dm^{2}$,则高是( )$dm$。
(3)若平行四边形的面积是$505\ m^{2}$,高是$20.2\ m$,则底是( )$m$。
(2)若平行四边形的底是$9.8\ dm$,面积是$117.6\ dm^{2}$,则高是( )$dm$。
(3)若平行四边形的面积是$505\ m^{2}$,高是$20.2\ m$,则底是( )$m$。
答案:
(1)25.2
(2)12
(3)25
(1)25.2
(2)12
(3)25
8. 16世纪末法国数学家韦达是第一个系统使用字母表示数的人,被称为“代数之父”。请解决问题:端午节,小红包8个粽子用了$a\ g$糯米,平均每个粽子用糯米( )$g$;当$a = 400$时,平均每个粽子用糯米( )$g$。
答案:
a÷8 50
9. 一个三角形的面积是$2.4\ m^{2}$,与它等底等高的平行四边形的面积是( )$m^{2}$。
答案:
4.8
10. 一个三角形与一个平行四边形的面积相等,高也相等,已知平行四边形的底是$18\ cm$,则三角形的底是( )$cm$。
答案:
36
二、判断题。(对的画“√”,错的画“×”。每小题2分,共10分)
1. 平行四边形的面积一定比梯形的面积大。 ( )
2. 两个面积相等的梯形可以拼成一个平行四边形。 ( )
3. $0.6是方程8x - 2x = 3.6$的解。 ( )
4. $3a + 5b = 8ab$ ( )
5. 平行四边形有无数条高,且每条高都相等。 ( )
1. 平行四边形的面积一定比梯形的面积大。 ( )
2. 两个面积相等的梯形可以拼成一个平行四边形。 ( )
3. $0.6是方程8x - 2x = 3.6$的解。 ( )
4. $3a + 5b = 8ab$ ( )
5. 平行四边形有无数条高,且每条高都相等。 ( )
答案:
1.× 2.× 3.√ 4.× 5.×
查看更多完整答案,请扫码查看


