《2025年多维互动提优课堂七年级数学上册苏科版》

1. 2的相反数是(B)
A.2
B.-2
C.$\frac{1}{2}$
D.2或-2

答案： 解：根据相反数的定义，只有符号不同的两个数互为相反数。2的相反数是-2。
答案：B

2. 在数轴上,到原点的距离小于2的点表示的整数的个数是(C)
A.1
B.2
C.3
D.5

答案： 解：在数轴上，到原点的距离小于2的点表示的数x满足|x| ＜ 2，即-2 ＜ x ＜ 2。其中的整数有-1，0，1，共3个。
答案：C

3. 下列各对数中,互为相反数的是(A)
A.$|-2|$和-2
B.$|-2|$和2
C.$-(-2)$和2
D.$|-2|和-(-2)$

答案： 解：A. $|-2| = 2$，2和-2互为相反数，符合题意。
B. $|-2| = 2$，2和2相等，不是相反数，不符合题意。
C. $-(-2) = 2$，2和2相等，不是相反数，不符合题意。
D. $|-2| = 2$，$-(-2) = 2$，2和2相等，不是相反数，不符合题意。
结论：A

4. 下列各数中,绝对值最小的是(C)
A.-3
B.$-\frac{2}{3}$
C.0
D.$\frac{5}{2}$

答案： 解：
A. $|-3| = 3$
B. $|-\frac{2}{3}| = \frac{2}{3}$
C. $|0| = 0$
D. $|\frac{5}{2}| = \frac{5}{2}$
比较大小：$0 ＜ \frac{2}{3} ＜ \frac{5}{2} ＜ 3$
答案：C

5. 在$-(-2)$,-2,0,1中,最小的数是(C)
A.0
B.$-(-2)$
C.-2
D.1

答案： 解：$-(-2)=2$
将各数按从小到大排列：$-2＜0＜1＜2$
最小的数是$-2$
答案：C

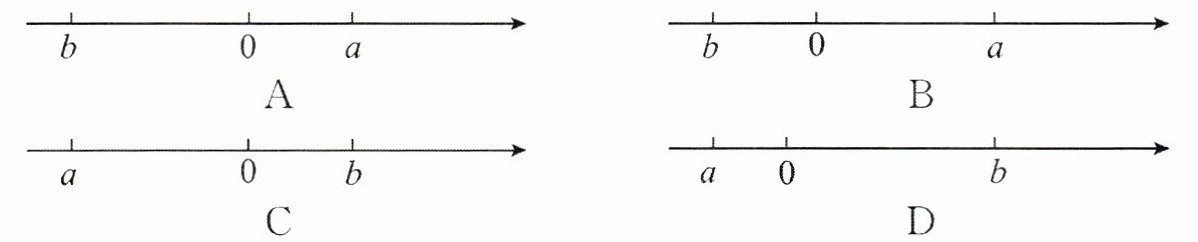
6. 已知a,b是有理数,$|a|= -a$,$|b|= b$,且$|a|＞|b|＞0$,用数轴上的点来表示a,b,正确的是(C)

答案： 【解析】：本题考查绝对值的意义及有理数在数轴上的表示。
根据绝对值的性质，正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0。
由题可知，$|a|=-a$，说明a是负数或者0（但在此题中，由于$|a|＞0$，所以a不能是0，只能是负数）。
同样，$|b|=b$，说明b是正数或者0（但在此题中，由于$|b|＞0$，所以b不能是0，只能是正数）。
再根据条件$|a|＞|b|＞0$，可以知道a的绝对值大于b的绝对值，且都大于0。
在数轴上，负数位于0的左侧，正数位于0的右侧。且绝对值越大的数，离0越远。
所以a应该在数轴上0的左侧且离0更远，b应该在数轴上0的右侧。
检查选项：
A选项中，a在0的右侧，b在0的左侧，与推理不符。
B选项中，虽然a在0的左侧，b在0的右侧，但b离0更远，与$|a|＞|b|$不符。
C选项中，a在0的左侧且离0更远，b在0的右侧，符合推理。
D选项中，a和b都在0的左侧，与推理不符。
因此，答案选C。
【答案】：C。

7. 数轴上表示数a,b的点如图所示,把a,-a,b,-b按照从小到大的顺序排列,正确的是(C)

A.$-b＜-a＜a＜b$
B.$-a＜-b＜a＜b$
C.$-b＜a＜-a＜b$
D.$-b＜b＜-a＜a$

答案： 解：由数轴可知，$a ＜ 0 ＜ b$，且$|a| ＜ |b|$。
$\because a ＜ 0$，$\therefore -a ＞ 0$；$\because b ＞ 0$，$\therefore -b ＜ 0$。
$\because |a| ＜ |b|$，$\therefore -a ＜ b$，$-b ＜ a$。
综上，$-b ＜ a ＜ -a ＜ b$。
答案：C

8. 下列各组有理数的大小比较中,正确的是(C)
A.$1＜-1$
B.$-\frac{8}{21}＜-\frac{3}{7}$
C.$-(-0.3)＜|-\frac{1}{3}|$
D.$-(-5)＜0$

答案： 解：
A. 正数大于负数，1 ＞ -1，A错误。
B. $ |-\frac{8}{21}| = \frac{8}{21} $，$ |-\frac{3}{7}| = \frac{9}{21} $，因为$ \frac{8}{21} ＜ \frac{9}{21} $，所以$ -\frac{8}{21} ＞ -\frac{3}{7} $，B错误。
C. $ -(-0.3) = 0.3 $，$ |-\frac{1}{3}| = \frac{1}{3} \approx 0.333 $，0.3 ＜ 0.333，C正确。
D. $ -(-5) = 5 $，5 ＞ 0，D错误。
结论：C