《2025年夺冠小状元课时作业本五年级数学上册苏教版》

例:如图,两个相同的直角梯形重叠在一起,求涂色部分的面积。

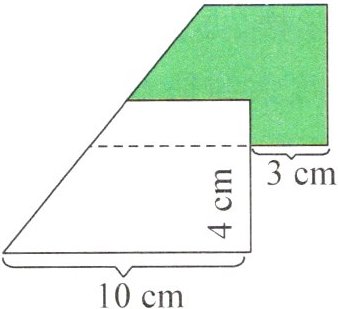
答案： 解析 两个直角梯形完全相同,即面积相等,则除去重叠部分,两个直角梯形剩下部分的面积也相等,所以求出下面直角梯形去除重叠部分剩下的空白部分的面积,也就是上面直角梯形去除重叠部分剩下的涂色部分的面积。
答案:10-3= 7(厘米)
(7+10)×4÷2= 34(平方厘米)
点评:解决此类无法直接计算面积的问题,可通过等积变换,将它转化为规则图形进行求解。

1. 如图,涂色三角形甲的面积比涂色三角形乙的面积大(18)平方分米。

答案： 18

2. 如图,正方形的边长是10厘米,三角形甲的面积比三角形乙的面积少20平方厘米,则线段BF的长是多少厘米?

答案： 10×10÷2+20=70(平方厘米)
70×2÷10=14(厘米)

3. 如图,已知长方形ABCD的面积是1200平方厘米,涂色部分的面积是750平方厘米,求四边形EFGO的面积。

答案： 750-1200÷2=150(平方厘米)

4. 如图,已知平行四边形ABCD的底是8分米,高是6分米,涂色部分的面积是16平方分米。求四边形EFGH的面积。(G是BD的中点)

答案： 16-8×6÷2÷2=4(平方分米)

5. 如图,在正方形ABCD中,AB= 40厘米,EC= 100厘米,求涂色部分的面积。

答案：
如图，连接FC。三角形FEC的面积为100×40÷2-40×40÷2=1200(平方厘米),FD的长为1200×2÷100=24(厘米),AF的长为40-24=16(厘米),涂色部分的面积为40×16÷2=320(平方厘米)。

6. 如图,四边形ABCD为长方形,AB= 10厘米,BC= 8厘米,E,F分别是AB,AD的中点,且FG= 2GE,涂色部分的面积是多少平方厘米?

答案： 10×8=80(平方厘米) 10÷2=5(厘米)
8÷2=4(厘米)
5×8÷2=20(平方厘米)
5×4÷2=10(平方厘米)
10×4÷2=20(平方厘米)
(80-20-20-10)÷3=10(平方厘米)