1. “正”字一共有(
5
)画,在整理数据时,4个“正”字表示的数据是(20
),数据45可以用(9
)个“正”字表示。
答案:
解析:
本题考查“正”字的笔画以及在统计数据中的应用。
首先,“正”字一共有5画,在统计数据时,一个“正”字代表5个单位。
接下来,我们来看4个“正”字表示的数据。由于一个“正”字代表5,那么4个“正”字就是4乘以5,即20。但这里需要注意,题目可能是问4个完整的“正”字(即每个“正”字都完整写了5笔)代表的数据,那么就是4乘以5等于20个单位,但考虑到“正”字在统计时通常代表5的倍数,如果4个“正”字是出现在统计表中,且每个“正”字都代表5个数据,则它们总共代表的数据是 $4 × 5 = 20$ 的5倍中的一个“组合”,实际代表的数据量应是 $4 × 5 = 20$(个数据中的每5个被一个“正”字所代表),直接算就是4个“正”字代表 $4 × 5 = 20$(个)单独的数据点,但在这个语境下,我们理解为4个“正”字代表的数量就是 $4 × 5 = 20$ 的直接结果,即20(但更准确的表述应是它们代表了20个单独的数据计数,若每个“正”代表5个的话)。但根据题目的直接询问和常规理解,我们只需回答4个“正”字表示的数据是20即可。但考虑到题目的实际意图可能是询问4个“正”字在统计中通常代表的数值(即每个“正”5个,4个就是20个中的“整数值”表示),且没有涉及更复杂的倍数或组合逻辑,所以直接回答20。但为了严谨,我们知道在具体情境中这代表20个单独的数据单位。而为了符合题目的直接询问,我们简化为:4个“正”字表示的数据是20(个单位)。但考虑到题目的实际教学背景和询问焦点,最终答案为4个“正”字表示的具体数值,即 $4 × 5 = 20$ 中的“20”所代表的直接数据量,也就是20(但理解为数据点或计数的总数)。而根据常规教学理解,我们直接回答20即可,这里的解释是为了更全面地理解背后的逻辑。实际答题时,学生只需知道4个“正”字代表20个数据单位。但题目更可能是问直接代表的数值,所以就是20。不过,如果数据是按群计数的(如每5个为一个“正”),则4个“正”直接代表的“群计数”下的数值就是它们所涵盖的总数,即20(但这里20就是直接答案,代表的数据量或计数量)。而数据45可以用几个“正”字表示,就是45除以5,得到9,所以可以用9个“正”字表示。
答案:
正字一共有5画,在整理数据时,4个“正”字表示的数据是20,数据45可以用9个“正”字表示。
本题考查“正”字的笔画以及在统计数据中的应用。
首先,“正”字一共有5画,在统计数据时,一个“正”字代表5个单位。
接下来,我们来看4个“正”字表示的数据。由于一个“正”字代表5,那么4个“正”字就是4乘以5,即20。但这里需要注意,题目可能是问4个完整的“正”字(即每个“正”字都完整写了5笔)代表的数据,那么就是4乘以5等于20个单位,但考虑到“正”字在统计时通常代表5的倍数,如果4个“正”字是出现在统计表中,且每个“正”字都代表5个数据,则它们总共代表的数据是 $4 × 5 = 20$ 的5倍中的一个“组合”,实际代表的数据量应是 $4 × 5 = 20$(个数据中的每5个被一个“正”字所代表),直接算就是4个“正”字代表 $4 × 5 = 20$(个)单独的数据点,但在这个语境下,我们理解为4个“正”字代表的数量就是 $4 × 5 = 20$ 的直接结果,即20(但更准确的表述应是它们代表了20个单独的数据计数,若每个“正”代表5个的话)。但根据题目的直接询问和常规理解,我们只需回答4个“正”字表示的数据是20即可。但考虑到题目的实际意图可能是询问4个“正”字在统计中通常代表的数值(即每个“正”5个,4个就是20个中的“整数值”表示),且没有涉及更复杂的倍数或组合逻辑,所以直接回答20。但为了严谨,我们知道在具体情境中这代表20个单独的数据单位。而为了符合题目的直接询问,我们简化为:4个“正”字表示的数据是20(个单位)。但考虑到题目的实际教学背景和询问焦点,最终答案为4个“正”字表示的具体数值,即 $4 × 5 = 20$ 中的“20”所代表的直接数据量,也就是20(但理解为数据点或计数的总数)。而根据常规教学理解,我们直接回答20即可,这里的解释是为了更全面地理解背后的逻辑。实际答题时,学生只需知道4个“正”字代表20个数据单位。但题目更可能是问直接代表的数值,所以就是20。不过,如果数据是按群计数的(如每5个为一个“正”),则4个“正”直接代表的“群计数”下的数值就是它们所涵盖的总数,即20(但这里20就是直接答案,代表的数据量或计数量)。而数据45可以用几个“正”字表示,就是45除以5,得到9,所以可以用9个“正”字表示。
答案:
正字一共有5画,在整理数据时,4个“正”字表示的数据是20,数据45可以用9个“正”字表示。
2. 玩游戏。
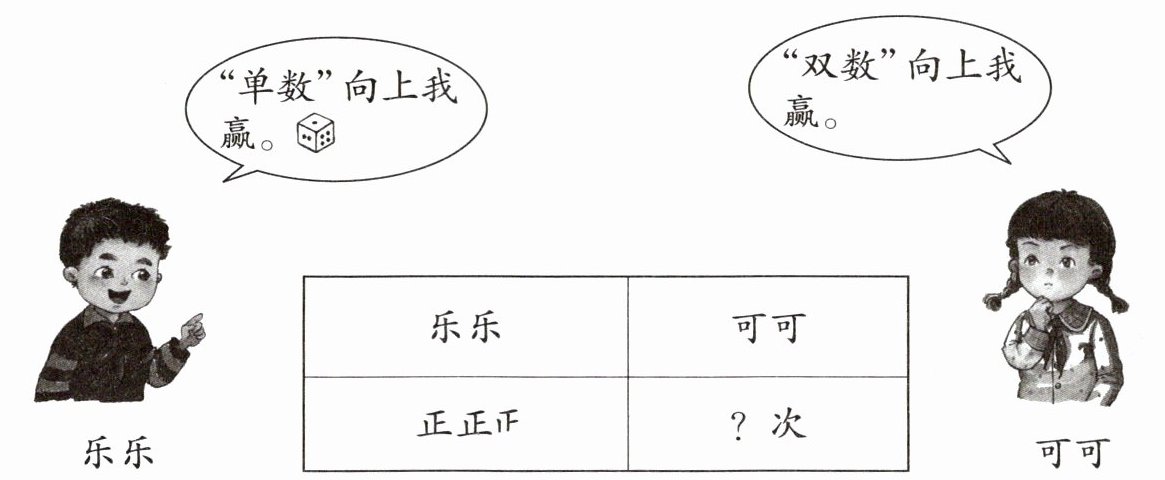
两人共掷了30次,乐乐赢了(

两人共掷了30次,乐乐赢了(
14
)次,可可赢了(16
)次。
答案:
乐乐赢的次数:“正正”是10次,“正”少一笔是4次,共10+4=14次。
可可赢的次数:30-14=16次。
14,16
可可赢的次数:30-14=16次。
14,16
3. 下面是某班同学的出生季节情况统计表。
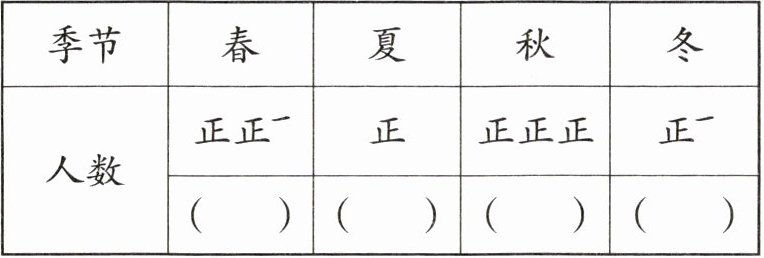
(1)请将统计表补充完整。
(2)根据上面的统计表把下面的统计图补充完整。
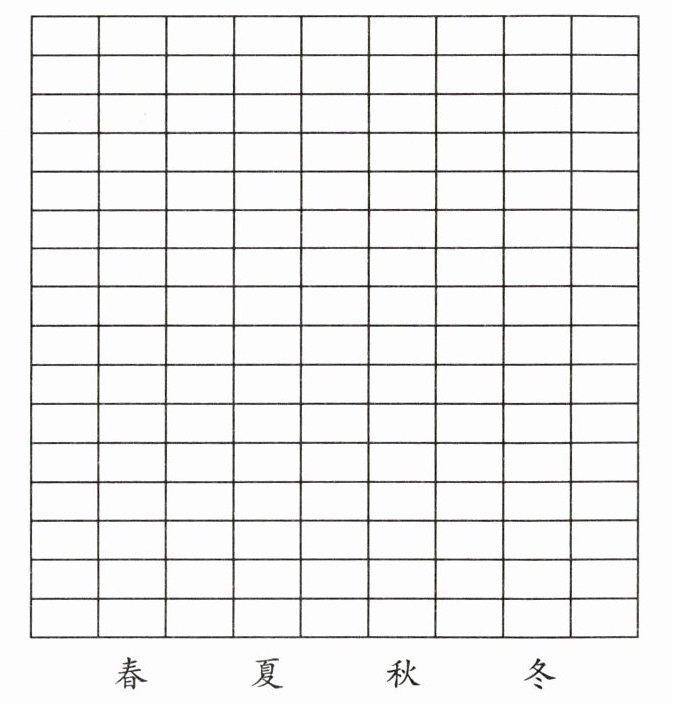
每个□表示1人。
(3)通过上图我们发现:(

(1)请将统计表补充完整。
(2)根据上面的统计表把下面的统计图补充完整。

每个□表示1人。
(3)通过上图我们发现:(
秋
)季出生的同学人数最多,( 夏
)季出生的同学人数最少。
答案:
解析:
本题考查对“正”字统计方法的掌握,通过数“正”字的笔画数或个数来计算对应的人数,进而完成统计表的填写、统计图的绘制以及对数据的分析。
(1)“正”字统计中,一个“正”字代表$5$人。
春季:有“正正一”,即$2×5 + 1= 11$人。
夏季:有“正”,即$5$人。
秋季:有“正正正”,即$3×5 = 15$人。
冬季:有“正一”,即$5 + 1 = 6$人。
答案:11;5;15;6。
(2)根据统计表中的数据,在统计图中对应季节的方格内涂色,因为每个□表示$1$人,所以春季涂$11$个方格,夏季涂$5$个方格,秋季涂$15$个方格,冬季涂$6$个方格。图略。
(3)比较各季节人数$15>11>6>5$,可知秋季出生的人数最多,夏季出生的人数最少。
答案:秋;夏。
本题考查对“正”字统计方法的掌握,通过数“正”字的笔画数或个数来计算对应的人数,进而完成统计表的填写、统计图的绘制以及对数据的分析。
(1)“正”字统计中,一个“正”字代表$5$人。
春季:有“正正一”,即$2×5 + 1= 11$人。
夏季:有“正”,即$5$人。
秋季:有“正正正”,即$3×5 = 15$人。
冬季:有“正一”,即$5 + 1 = 6$人。
答案:11;5;15;6。
(2)根据统计表中的数据,在统计图中对应季节的方格内涂色,因为每个□表示$1$人,所以春季涂$11$个方格,夏季涂$5$个方格,秋季涂$15$个方格,冬季涂$6$个方格。图略。
(3)比较各季节人数$15>11>6>5$,可知秋季出生的人数最多,夏季出生的人数最少。
答案:秋;夏。
查看更多完整答案,请扫码查看


