2025年轻松总复习暑假作业四年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松总复习暑假作业四年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
【典例1】画出下面三角形各指定底边上的高。
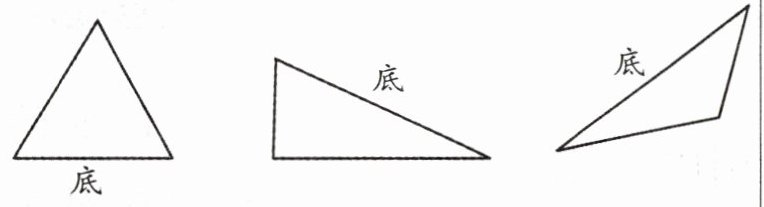

答案:
如图所示:
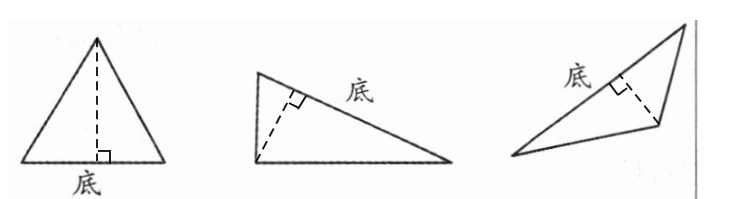
如图所示:

【典例2】明辨是非。
(1)用长分别是7cm,3cm和4cm的三根小棒可以拼成一个三角形。 (
(2)三根长度都是9cm的小棒一定可以拼成一个三角形。 (
(3)小明上学有3条路可到学校(如图),走中间的路最近。 (

(1)用长分别是7cm,3cm和4cm的三根小棒可以拼成一个三角形。 (
×
)(2)三根长度都是9cm的小棒一定可以拼成一个三角形。 (
√
)(3)小明上学有3条路可到学校(如图),走中间的路最近。 (
√
)
答案:
(1)×
(2)√
(3)√
(1)×
(2)√
(3)√
【典例3】把下列三角形的编号填在适当的括号内。

(

(
②③⑤
)是锐角三角形,(②⑤⑥
)是等腰三角形,(①④
)是直角三角形,(②
)是等边三角形,(⑥
)是钝角三角形。
答案:
(②③⑤)是锐角三角形,(②⑤⑥)是等腰三角形,(①④)是直角三角形,(②)是等边三角形,(⑥)是钝角三角形。
【典例4】在每个图形上画一条线段。
(1)将它分成两个锐角三角形。

(2)将它分成一个直角三角形和一个钝角三角形。
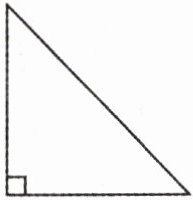
(1)将它分成两个锐角三角形。

(2)将它分成一个直角三角形和一个钝角三角形。

答案:
如图所示: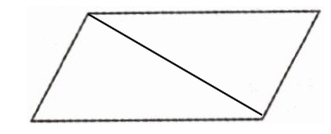
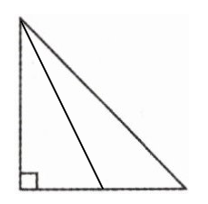
如图所示:


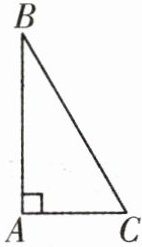
【典例5】在直角三角形ABC中,$∠A= 90^{\circ }$,$∠B×2= ∠C$,则$∠B= ?$,$∠C= ?$

答案:
解:在直角三角形ABC中,∠A=90°,
所以∠B+∠C=90°。
因为∠C=2∠B,
所以∠B+2∠B=90°,
3∠B=90°,
∠B=30°,
∠C=2∠B=60°。
∠B=30°,∠C=60°。
所以∠B+∠C=90°。
因为∠C=2∠B,
所以∠B+2∠B=90°,
3∠B=90°,
∠B=30°,
∠C=2∠B=60°。
∠B=30°,∠C=60°。
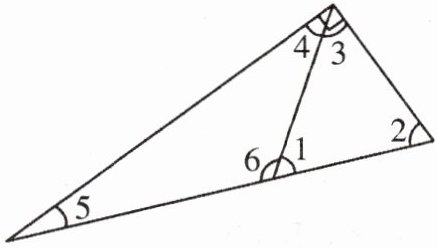
【典例6】下图中,$∠1= 58^{\circ }$,$∠2= 67^{\circ }$。$∠3$,$∠4$,$∠5$,$∠6$分别是多少度?

答案:
解:
在小三角形中,$∠1 + ∠2 + ∠3 = 180^{\circ}$,$∠3 = 180^{\circ} - ∠1 - ∠2 = 180^{\circ} - 58^{\circ} - 67^{\circ} = 55^{\circ}$。
$∠3 + ∠4 = 90^{\circ}$(假设存在直角),$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 55^{\circ} = 35^{\circ}$。
$∠2 + ∠5 = 90^{\circ}$(假设存在直角),$∠5 = 90^{\circ} - ∠2 = 90^{\circ} - 67^{\circ} = 23^{\circ}$。
$∠1 + ∠6 = 180^{\circ}$(平角定义),$∠6 = 180^{\circ} - ∠1 = 180^{\circ} - 58^{\circ} = 122^{\circ}$。
$∠3 = 55^{\circ}$,$∠4 = 35^{\circ}$,$∠5 = 23^{\circ}$,$∠6 = 122^{\circ}$。
在小三角形中,$∠1 + ∠2 + ∠3 = 180^{\circ}$,$∠3 = 180^{\circ} - ∠1 - ∠2 = 180^{\circ} - 58^{\circ} - 67^{\circ} = 55^{\circ}$。
$∠3 + ∠4 = 90^{\circ}$(假设存在直角),$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 55^{\circ} = 35^{\circ}$。
$∠2 + ∠5 = 90^{\circ}$(假设存在直角),$∠5 = 90^{\circ} - ∠2 = 90^{\circ} - 67^{\circ} = 23^{\circ}$。
$∠1 + ∠6 = 180^{\circ}$(平角定义),$∠6 = 180^{\circ} - ∠1 = 180^{\circ} - 58^{\circ} = 122^{\circ}$。
$∠3 = 55^{\circ}$,$∠4 = 35^{\circ}$,$∠5 = 23^{\circ}$,$∠6 = 122^{\circ}$。
查看更多完整答案,请扫码查看


