《2025年快乐之星假期培优暑假版五年级数学》

一、在三角形ABC中,已知$∠A= 90^{\circ },∠C= 60^{\circ },∠CBA= 30^{\circ }$。把三角形ABC绕点B按顺时针方向旋转一定角度后得到三角形$A'BC',∠C'BA= 90^{\circ }$(如图所示)。三角形ABC旋转了多少度?

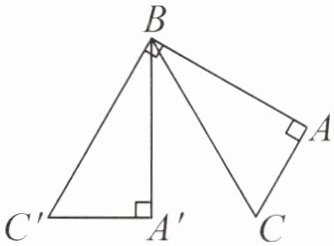
解：因为$\angle C'BA=90^{\circ}$，$\angle CBA=30^{\circ}$，
所以$\angle C'BC=\angle C'BA - \angle CBA=90^{\circ}-30^{\circ}=$$60^{\circ}$。
答：三角形$ABC$旋转了$60^{\circ}$。

答案： 解：因为$\angle C'BA=90^{\circ}$，$\angle CBA=30^{\circ}$，
所以$\angle C'BC=\angle C'BA - \angle CBA=90^{\circ}-30^{\circ}=60^{\circ}$。
答：三角形$ABC$旋转了$60^{\circ}$。

二、计算:$\frac {1}{2}+\frac {1}{6}+\frac {1}{12}+\frac {1}{20}+\frac {1}{30}+\frac {1}{42}+\frac {1}{56}+\frac {1}{72}+\frac {1}{90}$。

答案： $\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}$
$=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})+(\frac{1}{6}-\frac{1}{7})+(\frac{1}{7}-\frac{1}{8})+(\frac{1}{8}-\frac{1}{9})+(\frac{1}{9}-\frac{1}{10})$
$=1-\frac{1}{10}$
$=\frac{9}{10}$

三、已知$\frac {1}{18}= \frac {1}{A}+\frac {1}{B}+\frac {1}{C}$,A、B、C是不同的非0自然数,A、B、C分别是多少?

答案： 解：$\frac{1}{18}=\frac{1×(1+2+3)}{18×(1+2+3)}=\frac{1+2+3}{108}=\frac{1}{108}+\frac{2}{108}+\frac{3}{108}=\frac{1}{108}+\frac{1}{54}+\frac{1}{36}$
A、B、C分别是108、54、36。（答案不唯一）

四、规定△是一种新运算符号。已知$2△3= \frac {1}{2}+\frac {1}{3}+\frac {1}{4},3△4= \frac {1}{3}+\frac {1}{4}+\frac {1}{5}+\frac {1}{6}$,$4△5= \frac {1}{4}+\frac {1}{5}+\frac {1}{6}+\frac {1}{7}+\frac {1}{8}$,求下面各式的值。
(1)$6△2$$\frac{13}{42}$ (2)$4△3$$\frac{37}{60}$

答案：
(1) $6\triangle 2=\frac{1}{6}+\frac{1}{7}=\frac{13}{42}$
(2) $4\triangle 3=\frac{1}{4}+\frac{1}{5}+\frac{1}{6}=\frac{37}{60}$