《2025年学霸提优大试卷八年级物理上册苏科版》

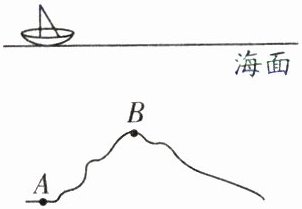
23. 海岭又称海底山脉,一般在海面以下,如图所示,某勘探船停在该海岭底部的A处正上方向海底发出声呐信号,6s后收到回波信号.之后勘探船以2km/h的平均速度沿直线行驶到达海岭最高点B处正上方,用时2h,该船再次向海底发出声呐信号,经3s后收到回波信号.已知声信号在海水中的传播速度为1500m/s.求:
(1)A处海水的深度;
(2)勘探船两次探测间航行的距离是多少?
(3)B处比A处高多少米?

答案：
(1)4500m　
(2)4000m　
(3)2250m
解析:
(1)由$v=\dfrac{s}{t}$可知，6s内声波传播的距离$s_{1}=v_{\text{声}}t_{1}=1500\ \text{m/s}×6\ \text{s}=9000\ \text{m}$，A处海水的深度$s_{A}=\dfrac{1}{2}s_{1}=\dfrac{1}{2}×9000\ \text{m}=4500\ \text{m}$.
(2)由$v=\dfrac{s}{t}$可得，勘探船两次探测间航行的距离$s=v_{\text{船}}t=2\ \text{km/h}×2\ \text{h}=4\ \text{km}=4000\ \text{m}$.
(3)由$v=\dfrac{s}{t}$可得，3s内声波传播的距离$s_{2}=v_{\text{声}}t_{2}=1500\ \text{m/s}×3\ \text{s}=4500\ \text{m}$，B处海水的深度$s_{B}=\dfrac{1}{2}s_{2}=\dfrac{1}{2}×4500\ \text{m}=2250\ \text{m}$，B处比A处高$\Delta s=s_{A}-s_{B}=4500\ \text{m}-2250\ \text{m}=2250\ \text{m}.$

24. 为了节能,某商场的自动扶梯安装了智能控制系统,在扶梯底端前3m处安装了如图1所示红外系统:乘客通过时,红外传感开关被触发,扶梯启动,同时计时器开始计时,若在设定时间t内无乘客通过顶端,扶梯将停止运行.已知扶梯长16m,从启动到匀速运行的v-t图像如图2所示,若乘客步行速度在0.5~1.5m/s之间.
(1)求乘客从红外杆处运动至扶梯底端的时间范围.
(2)为确保安全,设定时间t应至少为多少秒?

答案：
(1)2~6s　
(2)26s
解析:
(1)人步行的最小速度是0.5m/s，此时人从红外杆处走到扶梯底端所用的时间为$t_{1}=\dfrac{s_{1}}{v_{1}}=\dfrac{3\ \text{m}}{0.5\ \text{m/s}}=6\ \text{s}$，人步行的最大速度是1.5m/s，此时人从红外杆处走到扶梯底端所用的时间为$t_{2}=\dfrac{s_{1}}{v_{2}}=\dfrac{3\ \text{m}}{1.5\ \text{m/s}}=2\ \text{s}$.即乘客从红外杆处运动至扶梯底端的时间范围是2~6s.
(2)为确保安全，速度最慢的人也应安全乘坐扶梯到达顶端，故设定的时间至少为最慢的人全程运动的时间;由
(1)可知此时人从红外杆处走到扶梯所用的时间为$t_{1}=6\ \text{s}$，由图2可知，2s后扶梯匀速运动的速度是0.8m/s，故人乘坐扶梯从底端到顶端运动的时间为$t_{3}=\dfrac{s_{2}}{v_{3}}=\dfrac{16\ \text{m}}{0.8\ \text{m/s}}=20\ \text{s}$，故整个过程的总时间为$t_{\text{总}}=t_{1}+t_{3}=6\ \text{s}+20\ \text{s}=26\ \text{s}$，即设定时间应至少为26s.