《2025年名校课堂八年级物理上册人教版2河南专版》

1. (2024·郑州航空港区期末)河南省三门峡市湖滨区陕州故城(陕县老城)东南部,有一座距今已有800余年的宝轮寺塔,俗称“蛤蟆塔”,是我国现存四大回音建筑之一,因在塔旁击掌有蛤蟆式回音而得名。击掌后,部分声波先后被高度不同的各层塔檐反射会聚,返回地面,组成一个类似蛙鸣的回声。

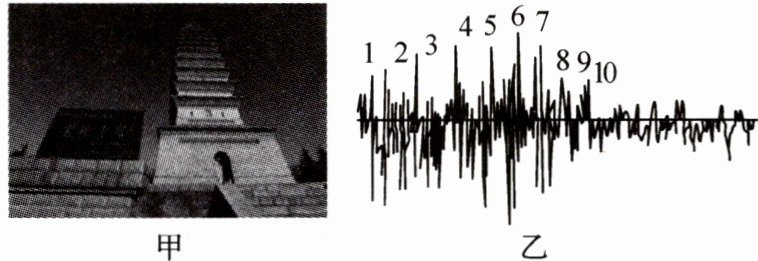
(1)图乙是某次实验时回声的波形图,图中编号1-10为不同塔檐的回声,其中声音最响亮的是编号6。
(2)隧道中有超速抓拍的摄像头(限速60km/h),当小明的车距离前方测速仪370m时,测速仪发出超声波信号,信号碰到小明的车后返回,测速仪从发出到接收到信号用时2s,请问小明的车是否超速行驶?(已知声音在空气中的传播速度为340m/s)

答案： 1.
(1)6 解:
(2)信号发出到碰到小明的车所用时间:
$t=\frac {1}{2}×2s=1s$
信号在1s内通过的距离:
$s=vt=340m/s×1s=340m$
汽车通过的距离:
$s'=s_{0}-s=370m-340m=30m$
汽车的速度:
$v_{车}=\frac {s'}{t}=\frac {30m}{1s}=30m/s=108km/h＞60km/h$
故小明的车超速行驶。

2. 如图所示为一款身高测量仪,其顶部的感应器竖直向下发射超声波信号,经下方物体反射后返回,被感应器接收。已知感应器距测高台的距离为2.38m,超声波在空气中的速度为340m/s。
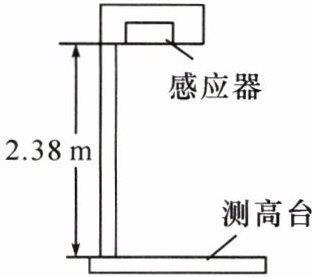
(1)无人站立在测高台上时,求感应器发射超声波后到达测高台的时间。
(2)某同学站在测高台上,感应器记录信号从发射到接收所经历的时间为0.005s,求该同学的身高。

答案： 2.解:
(1)由$v=\frac {s}{t}$可得,感应器发射超声波后到达测高台的
时间:
$t=\frac {s}{v}=\frac {2.38m}{340m/s}=0.007s$
(2)$t_{测}=0.005s$时,超声波从感应器到该同学头部的传播
时间:
$t'=\frac {1}{2}t_{测}=\frac {1}{2}×0.005s=2.5×10^{-3}s$
由$v=\frac {s}{t}$可得,感应器到该同学头部的距离:
$s'=vt'=340m/s×2.5×10^{-3}s=0.85m$
该同学的身高:
$h=s-s'=2.38m-0.85m=1.53m$

3. 清华附中校本经典题如图所示,我国有些地方修筑了“音乐公路”。当汽车以一定速度匀速行驶时,就会奏出一段悦耳的乐曲。公路凹槽的疏密可以根据乐曲的音调高低来设计,假设汽车行驶速度是54km/h。
(1)若公路的全长为1.08km,求该汽车通过此公路所需的时间。
(2)第一个音符“sol”的频率为400Hz,汽车发出这个音时,求所对应的相邻凹槽之间的距离。

答案： 3.解:
(1)汽车通过音乐公路所需时间:
$t_{1}=\frac {s_{1}}{v}=\frac {1.08km}{54km/h}=0.02h=72s$
(2)汽车发出音符“sol”的时间为$t_{2}=\frac {1}{400}s$,所对应的相邻凹槽
之间的距离:
$s_{2}=vt_{2}=\frac {54}{3.6}m/s×\frac {1}{400}s=0.0375m$