《2025年暑假作业本大象出版社七年级数学人教版》

10. 如图7-27,把一个长方形纸片沿EF折叠后,点D,C分别落在点$D',C'$的位置.若$∠EFB= 60^{\circ }$,则$∠AED'$的度数为(C)
A.$50^{\circ }$
B.$55^{\circ }$
C.$60^{\circ }$
D.$65^{\circ }$

答案： C

11. 如果$∠α与∠β$的两边分别平行,$∠α比∠β$的3倍少$36^{\circ }$,那么$∠α$的度数是(C)
A.$18^{\circ }$
B.$126^{\circ }$
C.$18^{\circ }或126^{\circ }$
D.以上都不对

答案： C 提示:
∵ $\angle\alpha$与$\angle\beta$的两边分别平行，
∴ $\angle\alpha$与$\angle\beta$相等或互补。设$\angle\alpha = x^{\circ}$。
∵ $\angle\alpha$比$\angle\beta$的3倍少$36^{\circ}$，
∴ 若$\angle\alpha$与$\angle\beta$相等，则$x = 3x - 36$，解得$x = 18$；
若$\angle\alpha$与$\angle\beta$互补，则$x = 3(180 - x) - 36$，解得$x = 126$。
∴ $\angle\alpha$的度数是$18^{\circ}$或$126^{\circ}$。

证明:∵$HG// AB$(已知),
∴$∠1= ∠3$(两直线平行，内错角相等).
又∵$HG// CD$(已知),
∴$∠2= ∠4$(两直线平行，内错角相等).
∵$AB// CD$(已知),
∴$∠BEF+$$∠EFD$$=180^{\circ }$(两直线平行，同旁内角互补).
又∵EG平分$∠BEF$(已知),
∴$∠1= \frac {1}{2}∠$$BEF$(角平分线的定义).
又∵FG平分$∠EFD$(已知),
∴$∠2= \frac {1}{2}∠$$EFD$(角平分线的定义).
∴$∠1+∠2= \frac {1}{2}$($∠BEF$+$∠EFD$).
∴$∠1+∠2= 90^{\circ }$.
∴$∠3+∠4= 90^{\circ }$(等量代换),
即$∠EGF= 90^{\circ }$.

答案： 两直线平行，内错角相等 两直线平行，内错角相等 $\angle EFD$ 两直线平行，同旁内角互补 $BEF$ 角平分线的定义 $EFD$ 角平分线的定义 $\angle BEF$ $\angle EFD$ 等量代换

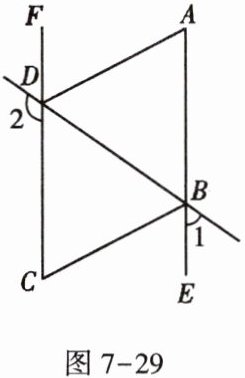
13. 如图7-29,已知$∠1+∠2= 180^{\circ },∠A= ∠C$,BC平分$∠DBE$.
(1)AE与FC平行吗?请说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)DA平分$∠BDF$吗?为什么?

答案：

(1)$AE$与$FC$平行。理由如下:
∵ $\angle 1+\angle 2 = 180^{\circ}$，$\angle 2+\angle BDC = 180^{\circ}$，
∴ $\angle BDC = \angle 1$。
∴ $AE// FC$。
(2)$AD$与$BC$平行。
∵ $AE// FC$，
∴ $\angle C+\angle ABC = 180^{\circ}$。
∵ $\angle A = \angle C$，
∴ $\angle A+\angle ABC = 180^{\circ}$。
∴ $AD// BC$。
(3)$DA$平分$\angle BDF$。如图所示，

∵ $BC$平分$\angle DBE$，
∴ $\angle 3 = \angle 4$。
∵ $AD// BC$，$AE// FC$，
∴ $\angle 4 = \angle 6$，$\angle A = \angle 5$，$\angle 3 = \angle C$。
又
∵ $\angle A = \angle C$，
∴ $\angle 5 = \angle 6$。
∴ $DA$平分$\angle BDF$。