第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
13. 新考向 某校计划为元旦晚会购买一批销售单价为 12 元的商品作为抽奖奖品,供货商提供两种供货方案.
方案一:若购买超过 20 件,超过部分按标价打八折出售;
方案二:若购买超过 15 件,所有商品每件让利 1 元,且超过部分按标价打九折出售.
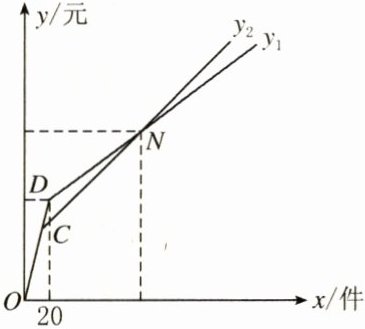
设购买奖品的数量为$x$件,按方案一购买所需的费用为$y_{1}$元,按方案二购买所需的费用为$y_{2}$元,函数图象如右下图所示.
(1)请分别求出$y_{1},y_{2}$关于$x$的函数表达式;
(2)求点$N$的坐标,并指出点$N$表示的实际意义;
(3)若学校购买这批奖品的预算为 1600 元,则方案____
方案一:若购买超过 20 件,超过部分按标价打八折出售;
方案二:若购买超过 15 件,所有商品每件让利 1 元,且超过部分按标价打九折出售.
设购买奖品的数量为$x$件,按方案一购买所需的费用为$y_{1}$元,按方案二购买所需的费用为$y_{2}$元,函数图象如右下图所示.
(1)请分别求出$y_{1},y_{2}$关于$x$的函数表达式;
(2)求点$N$的坐标,并指出点$N$表示的实际意义;
(3)若学校购买这批奖品的预算为 1600 元,则方案____
一
更合算(填“一”或“二”).
答案:
解:
(1) 当 $0\leq x\leq 20$ 时,$y_1 = 12x$;当 $x\gt 20$ 时,$y_1 = 20\times 12 + (x - 20)\times 12\times 0.8 = 9.6x + 48$。当 $0\leq x\leq 15$ 时,$y_2 = 12x$;当 $x\gt 15$ 时,$y_2 = 15\times 12 + (x - 15)\times 12\times 0.9 - x\times 1 = 9.8x + 18$。综上所述:$y_1 = \begin{cases}12x, & 0\leq x\leq 20, \\ 9.6x + 48, & x\gt 20.\end{cases}$ $y_2 = \begin{cases}12x, & 0\leq x\leq 15, \\ 9.8x + 18, & x\gt 15.\end{cases}$
(2) 令 $9.6x + 48 = 9.8x + 18$,解得 $x = 150$。对于 $y_1 = 9.6x + 48$,当 $x = 150$ 时,$y = 1488$,故点 $N$ 的坐标为 $(150, 1488)$。点 $N$ 表示的实际意义:当该校购买 150 件奖品时,按方案一和按方案二购买所需费用一样多,为 1488 元。
(3) -
(1) 当 $0\leq x\leq 20$ 时,$y_1 = 12x$;当 $x\gt 20$ 时,$y_1 = 20\times 12 + (x - 20)\times 12\times 0.8 = 9.6x + 48$。当 $0\leq x\leq 15$ 时,$y_2 = 12x$;当 $x\gt 15$ 时,$y_2 = 15\times 12 + (x - 15)\times 12\times 0.9 - x\times 1 = 9.8x + 18$。综上所述:$y_1 = \begin{cases}12x, & 0\leq x\leq 20, \\ 9.6x + 48, & x\gt 20.\end{cases}$ $y_2 = \begin{cases}12x, & 0\leq x\leq 15, \\ 9.8x + 18, & x\gt 15.\end{cases}$
(2) 令 $9.6x + 48 = 9.8x + 18$,解得 $x = 150$。对于 $y_1 = 9.6x + 48$,当 $x = 150$ 时,$y = 1488$,故点 $N$ 的坐标为 $(150, 1488)$。点 $N$ 表示的实际意义:当该校购买 150 件奖品时,按方案一和按方案二购买所需费用一样多,为 1488 元。
(3) -
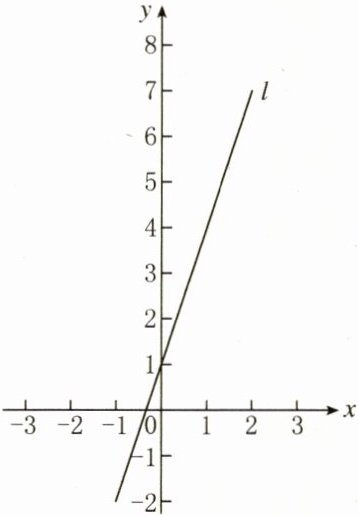
14. 学科素养 下表中的两组对应值满足一次函数$y=kx+b$,现画出了它的图象为直线$l$,如下图所示. 某同学为观察$k,b$对图象的影响,将上面函数中的$k$与$b$交换位置后得到另一个一次函数,设其图象为直线$l'$.
(1)求直线$l$的函数表达式;
(2)请在图上画出直线$l'$(不要求列表计算),并求直线$l'$被直线$l$和$y$轴所截线段的长.
|$x$|-1|0|
|----|----|----|
|$y$|-2|1|
(1)求直线$l$的函数表达式;
(2)请在图上画出直线$l'$(不要求列表计算),并求直线$l'$被直线$l$和$y$轴所截线段的长.
|$x$|-1|0|
|----|----|----|
|$y$|-2|1|

答案:
解:
(1) 在 $y = kx + b$ 中,当 $x = -1$ 时,$y = -2$,即 $-k + b = -2$;当 $x = 0$ 时,$y = 1$,即 $b = 1$,将 $b = 1$ 代入 $-k + b = -2$,得 $k = 3$,
∴ 直线 $l$ 的函数表达式为 $y = 3x + 1$。
(2)
∵ 直线 $l$ 的函数表达式为 $y = 3x + 1$,
∴ 直线 $l'$ 的函数表达式为 $y = x + 3$。如图,$l'$ 为所画直线。由 $x + 3 = 3x + 1$,得 $x = 1$,
∴ $y = 3\times 1 + 1 = 4$,
∴ 两直线的交点为 $(1, 4)$。
∵ 直线 $l'$:$y = x + 3$ 与 $y$ 轴的交点为 $(0, 3)$,
∴ 直线 $l'$ 被直线 $l$ 和 $y$ 轴所截线段的长为 $\sqrt{1^2 + (4 - 3)^2} = \sqrt{2}$
解:
(1) 在 $y = kx + b$ 中,当 $x = -1$ 时,$y = -2$,即 $-k + b = -2$;当 $x = 0$ 时,$y = 1$,即 $b = 1$,将 $b = 1$ 代入 $-k + b = -2$,得 $k = 3$,
∴ 直线 $l$ 的函数表达式为 $y = 3x + 1$。
(2)
∵ 直线 $l$ 的函数表达式为 $y = 3x + 1$,
∴ 直线 $l'$ 的函数表达式为 $y = x + 3$。如图,$l'$ 为所画直线。由 $x + 3 = 3x + 1$,得 $x = 1$,
∴ $y = 3\times 1 + 1 = 4$,
∴ 两直线的交点为 $(1, 4)$。
∵ 直线 $l'$:$y = x + 3$ 与 $y$ 轴的交点为 $(0, 3)$,
∴ 直线 $l'$ 被直线 $l$ 和 $y$ 轴所截线段的长为 $\sqrt{1^2 + (4 - 3)^2} = \sqrt{2}$

查看更多完整答案,请扫码查看


