《2025年假日数学吉林出版集团股份有限公司五年级人教版》

7. 解方程。
$x-\frac {1}{2}= \frac {4}{5}$，$x=$$\frac{13}{10}$
$\frac {1}{6}+x= \frac {1}{2}$，$x=$$\frac{1}{3}$
$x-\frac {5}{6}= \frac {1}{6}$，$x=$1
$x-\frac {4}{5}= \frac {5}{12}$，$x=$$\frac{73}{60}$
$x+\frac {3}{7}= \frac {3}{4}$，$x=$$\frac{9}{28}$
$x-\frac {5}{12}= \frac {3}{8}$，$x=$$\frac{19}{24}$

答案： $x=\frac{13}{10}$ $x=\frac{1}{3}$ $x=1$ $x=\frac{73}{60}$ $x=\frac{9}{28}$ $x=\frac{19}{24}$

8. 画出图形A绕点O逆时针旋转$90^{\circ }$后的图形。

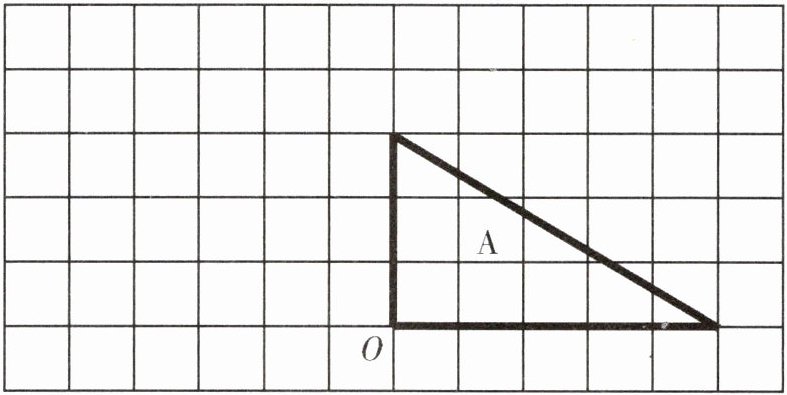
本题可根据图形旋转的性质，通过确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点，再顺次连接对应点得到旋转后的图形。
步骤一：明确图形旋转的性质
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。图形旋转后，对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。
步骤二：确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点
对于直角顶点（除$O$点外），设其坐标为$(x,y)$（以$O$为原点建立坐标系），绕点$O$逆时针旋转$90^{\circ}$后，根据旋转坐标变化规律（$(x,y)$绕原点逆时针旋转$90^{\circ}$变为$(-y,x)$），可得到其对应点坐标。
点$O$为旋转中心，旋转后位置不变。
步骤三：顺次连接对应点
根据上述方法确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点后，用线段顺次连接这些对应点，即可得到图形$A$绕点$O$逆时针旋转$90^{\circ}$后的图形。
（由于无法直接绘制图形，你可以根据上述方法在给定的方格图中进行绘制：先找到三角形$A$除$O$点外的另一个顶点，将其绕$O$点逆时针旋转$90^{\circ}$（在方格图中表现为向上移动与原来横向距离相同的格数，再向左移动与原来纵向距离相同的格数），然后连接$O$点与旋转后的点，得到旋转后的三角形。）
综上，按照图形旋转的性质和方法，可画出图形$A$绕点$O$逆时针旋转$90^{\circ}$后的图形。

答案： 本题可根据图形旋转的性质，通过确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点，再顺次连接对应点得到旋转后的图形。
步骤一：明确图形旋转的性质
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。图形旋转后，对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。
步骤二：确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点
对于直角顶点（除$O$点外），设其坐标为$(x,y)$（以$O$为原点建立坐标系），绕点$O$逆时针旋转$90^{\circ}$后，根据旋转坐标变化规律（$(x,y)$绕原点逆时针旋转$90^{\circ}$变为$(-y,x)$），可得到其对应点坐标。
点$O$为旋转中心，旋转后位置不变。
步骤三：顺次连接对应点
根据上述方法确定图形$A$各顶点绕点$O$逆时针旋转$90^{\circ}$后的对应点后，用线段顺次连接这些对应点，即可得到图形$A$绕点$O$逆时针旋转$90^{\circ}$后的图形。
（由于无法直接绘制图形，你可以根据上述方法在给定的方格图中进行绘制：先找到三角形$A$除$O$点外的另一个顶点，将其绕$O$点逆时针旋转$90^{\circ}$（在方格图中表现为向上移动与原来横向距离相同的格数，再向左移动与原来纵向距离相同的格数），然后连接$O$点与旋转后的点，得到旋转后的三角形。）
综上，按照图形旋转的性质和方法，可画出图形$A$绕点$O$逆时针旋转$90^{\circ}$后的图形。

9. 把一个铁块放入一个长方体水桶里,铁块完全浸没在水中(水未溢出),水面升高4cm,水桶底面是边长为40cm的正方形。求铁块的体积。

答案： $6400cm^{3}$