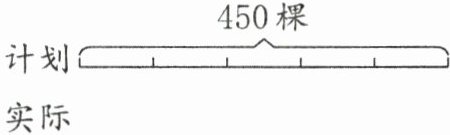
2. 丰盛果园今年计划培育450棵果树苗,受今年气候影响,实际培育的棵数比计划少了$\frac {1}{5}$,实际培育了多少棵果树苗? (先把线段图补充完整,再解答)(6分)

答案:
解析:本题考查了分数乘法的实际应用,关键在于找出实际培育棵数与计划培育棵数之间的数量关系,通过计划培育棵数以及实际比计划少的比例来计算实际培育的棵数。
线段图补充如下(图略,描述为):在表示计划的线段下方,画一条长度为计划线段长度的$\frac{4}{5}$的线段表示实际培育的棵数。
解答:
$450×(1 - \frac{1}{5})$
$= 450×\frac{4}{5}$
$= 360$(棵)
答:实际培育了360棵果树苗。
线段图补充如下(图略,描述为):在表示计划的线段下方,画一条长度为计划线段长度的$\frac{4}{5}$的线段表示实际培育的棵数。
解答:
$450×(1 - \frac{1}{5})$
$= 450×\frac{4}{5}$
$= 360$(棵)
答:实际培育了360棵果树苗。
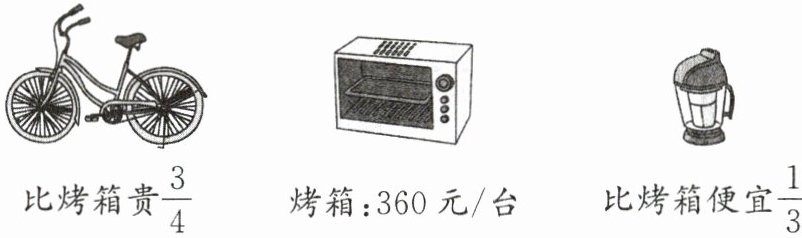
3. 商场中自行车、烤箱、豆浆机的价钱信息如图所示,自行车、豆浆机的单价各是多少元? (6分)

答案:
解析:本题考查分数乘除法的应用。
自行车价格:
已知烤箱价格是$360$元,自行车比烤箱贵$\frac{3}{4}$,
把烤箱价格看作单位$1$,则自行车价格是烤箱价格的$1 + \frac{3}{4}=\frac{7}{4}$。
根据分数乘法的意义,自行车价格为$360×\frac{7}{4} = 630×\frac{4}{4}×\frac{7}{4}=630×1×\frac{7}{4}=630÷4×7 = 630×\frac{7}{4}= 630÷(4÷7)=630÷\frac{4}{7}= 90×7 = 630$(元)。
豆浆机价格:
已知豆浆机比烤箱便宜$\frac{1}{3}$,把烤箱价格看作单位$1$,
则豆浆机价格是烤箱价格的$1 - \frac{1}{3}=\frac{2}{3}$。
根据分数乘法的意义,豆浆机价格为$360×\frac{2}{3} = 240$(元)。
答案:自行车单价是$630$元,豆浆机单价是$240$元。
自行车价格:
已知烤箱价格是$360$元,自行车比烤箱贵$\frac{3}{4}$,
把烤箱价格看作单位$1$,则自行车价格是烤箱价格的$1 + \frac{3}{4}=\frac{7}{4}$。
根据分数乘法的意义,自行车价格为$360×\frac{7}{4} = 630×\frac{4}{4}×\frac{7}{4}=630×1×\frac{7}{4}=630÷4×7 = 630×\frac{7}{4}= 630÷(4÷7)=630÷\frac{4}{7}= 90×7 = 630$(元)。
豆浆机价格:
已知豆浆机比烤箱便宜$\frac{1}{3}$,把烤箱价格看作单位$1$,
则豆浆机价格是烤箱价格的$1 - \frac{1}{3}=\frac{2}{3}$。
根据分数乘法的意义,豆浆机价格为$360×\frac{2}{3} = 240$(元)。
答案:自行车单价是$630$元,豆浆机单价是$240$元。
4. 《汉书》,又称《前汉书》,是我国第一部纪传体断代史,包括“纪”“表”“志”“传”四种文体,共100篇。“纪”占全书篇数的$\frac {3}{25}$,“传”占全书篇数的$\frac {7}{10}$,那么“表”和“志”一共有多少篇? (6分)
答案:
解析:
本题考查的是分数的运算。
由题意知,“纪”占全书篇数的$\frac{3}{25}$,“传”占全书篇数的$\frac{7}{10}$。
所以“纪”的篇数为:
$100×\frac{3}{25}=12$(篇),
“传”的篇数为:
$100×\frac{7}{10}=70$(篇),
“表”和“志”的篇数为:
$100-12-70=18$(篇)。
答案:
“表”和“志”一共有18篇。
本题考查的是分数的运算。
由题意知,“纪”占全书篇数的$\frac{3}{25}$,“传”占全书篇数的$\frac{7}{10}$。
所以“纪”的篇数为:
$100×\frac{3}{25}=12$(篇),
“传”的篇数为:
$100×\frac{7}{10}=70$(篇),
“表”和“志”的篇数为:
$100-12-70=18$(篇)。
答案:
“表”和“志”一共有18篇。
5. “冬季两项”是传统冰雪项目,它是将越野滑雪和射击相结合的运动。男子个人比赛的全长是20千米,每滑行全长的$\frac {1}{5}$就停下射击1次(不包括终点),示意图如图所示。当一名男运动员在比赛中完成第3次射击时,他还要滑行多少千米才能到达终点? (7分)


答案:
本题可先求出完成第$3$次射击时滑行的路程占全长的比例,进而求出此时滑行的路程,最后用总路程减去已滑行的路程,即可得到还要滑行的路程。
步骤一:计算完成第$3$次射击时滑行的路程占全长的比例
已知每滑行全长的$\frac{1}{5}$就停下射击$1$次,那么完成第$3$次射击时,滑行的路程占全长的比例为:
$\frac{1}{5}×3 = \frac{3}{5}$
步骤二:计算完成第$3$次射击时滑行的路程
已知男子个人比赛的全长是$20$千米,根据“求一个数的几分之几是多少用乘法”,可得完成第$3$次射击时滑行的路程为:
$20×\frac{3}{5}= 12$(千米)
步骤三:计算还要滑行的路程
用总路程减去完成第$3$次射击时滑行的路程,可得还要滑行的路程为:
$20 - 12 = 8$(千米)
综上,他还要滑行$8$千米才能到达终点。
步骤一:计算完成第$3$次射击时滑行的路程占全长的比例
已知每滑行全长的$\frac{1}{5}$就停下射击$1$次,那么完成第$3$次射击时,滑行的路程占全长的比例为:
$\frac{1}{5}×3 = \frac{3}{5}$
步骤二:计算完成第$3$次射击时滑行的路程
已知男子个人比赛的全长是$20$千米,根据“求一个数的几分之几是多少用乘法”,可得完成第$3$次射击时滑行的路程为:
$20×\frac{3}{5}= 12$(千米)
步骤三:计算还要滑行的路程
用总路程减去完成第$3$次射击时滑行的路程,可得还要滑行的路程为:
$20 - 12 = 8$(千米)
综上,他还要滑行$8$千米才能到达终点。
附加题。(共10分)
计算$(\frac {1}{16}+\frac {1}{26}+\frac {1}{36}+\frac {1}{46})×(\frac {1}{26}+\frac {1}{36}+\frac {1}{46}+\frac {1}{56})-(\frac {1}{16}+\frac {1}{26}+\frac {1}{36}+\frac {1}{46}+\frac {1}{56})×(\frac {1}{26}+\frac {1}{36}+\frac {1}{46})$的结果是( )。
计算$(\frac {1}{16}+\frac {1}{26}+\frac {1}{36}+\frac {1}{46})×(\frac {1}{26}+\frac {1}{36}+\frac {1}{46}+\frac {1}{56})-(\frac {1}{16}+\frac {1}{26}+\frac {1}{36}+\frac {1}{46}+\frac {1}{56})×(\frac {1}{26}+\frac {1}{36}+\frac {1}{46})$的结果是( )。
答案:
解析:本题可通过换元法简化计算。设$a = \frac{1}{26}+\frac{1}{36}+\frac{1}{46}$,$b=\frac{1}{26}+\frac{1}{36}+\frac{1}{46}+\frac{1}{56}$,则原式可转化为$(\frac{1}{16}+a)×b - (\frac{1}{16}+b)×a$,然后展开式子进行化简计算。
答案:
设$a = \frac{1}{26}+\frac{1}{36}+\frac{1}{46}$,$b=\frac{1}{26}+\frac{1}{36}+\frac{1}{46}+\frac{1}{56}$。
$(\frac{1}{16}+a)×b - (\frac{1}{16}+b)×a$
$=\frac{1}{16}b + ab - (\frac{1}{16}a + ab)$
$=\frac{1}{16}b + ab - \frac{1}{16}a - ab$
$=\frac{1}{16}(b - a)$
把$a = \frac{1}{26}+\frac{1}{36}+\frac{1}{46}$,$b=\frac{1}{26}+\frac{1}{36}+\frac{1}{46}+\frac{1}{56}$代入$\frac{1}{16}(b - a)$可得:
$\frac{1}{16}×\frac{1}{56}=\frac{1}{896}$
故答案为$\frac{1}{896}$。
答案:
设$a = \frac{1}{26}+\frac{1}{36}+\frac{1}{46}$,$b=\frac{1}{26}+\frac{1}{36}+\frac{1}{46}+\frac{1}{56}$。
$(\frac{1}{16}+a)×b - (\frac{1}{16}+b)×a$
$=\frac{1}{16}b + ab - (\frac{1}{16}a + ab)$
$=\frac{1}{16}b + ab - \frac{1}{16}a - ab$
$=\frac{1}{16}(b - a)$
把$a = \frac{1}{26}+\frac{1}{36}+\frac{1}{46}$,$b=\frac{1}{26}+\frac{1}{36}+\frac{1}{46}+\frac{1}{56}$代入$\frac{1}{16}(b - a)$可得:
$\frac{1}{16}×\frac{1}{56}=\frac{1}{896}$
故答案为$\frac{1}{896}$。
查看更多完整答案,请扫码查看


