3. 解方程。(9分)
$\frac {5}{7}x÷\frac {5}{14}= \frac {7}{8}$ $\frac {2}{3}x+\frac {1}{6}x= 15$ $1-\frac {1}{3}x= \frac {1}{6}$
$\frac {5}{7}x÷\frac {5}{14}= \frac {7}{8}$ $\frac {2}{3}x+\frac {1}{6}x= 15$ $1-\frac {1}{3}x= \frac {1}{6}$
答案:
3.
第一个方程:$\frac {5}{7}x ÷ \frac {5}{14} = \frac {7}{8}$
$\frac {5}{7}x = \frac {7}{8} × \frac {5}{14}$
$\frac {5}{7}x = \frac {5}{16}$
$x = \frac {5}{16} ÷ \frac {5}{7}$
$x = \frac {7}{16}$
第二个方程:$\frac {2}{3}x + \frac {1}{6}x = 15$
$\frac {4}{6}x + \frac {1}{6}x = 15$
$\frac {5}{6}x = 15$
$x = 15 ÷ \frac {5}{6}$
$x = 18$
第三个方程:$1 - \frac {1}{3}x = \frac {1}{6}$
$\frac {1}{3}x = 1 - \frac {1}{6}$
$\frac {1}{3}x = \frac {5}{6}$
$x = \frac {5}{6} ÷ \frac {1}{3}$
$x = \frac {5}{2}$
第一个方程:$\frac {5}{7}x ÷ \frac {5}{14} = \frac {7}{8}$
$\frac {5}{7}x = \frac {7}{8} × \frac {5}{14}$
$\frac {5}{7}x = \frac {5}{16}$
$x = \frac {5}{16} ÷ \frac {5}{7}$
$x = \frac {7}{16}$
第二个方程:$\frac {2}{3}x + \frac {1}{6}x = 15$
$\frac {4}{6}x + \frac {1}{6}x = 15$
$\frac {5}{6}x = 15$
$x = 15 ÷ \frac {5}{6}$
$x = 18$
第三个方程:$1 - \frac {1}{3}x = \frac {1}{6}$
$\frac {1}{3}x = 1 - \frac {1}{6}$
$\frac {1}{3}x = \frac {5}{6}$
$x = \frac {5}{6} ÷ \frac {1}{3}$
$x = \frac {5}{2}$
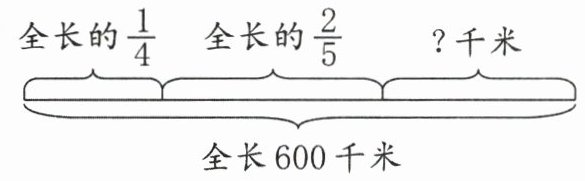
4. 看图列式计算。(8分)
(1)
(2)
(1)

(2)

答案:
(1) $600×\left(1-\frac{1}{4}-\frac{2}{5}\right)=600×\frac{7}{20}=210$(千米)
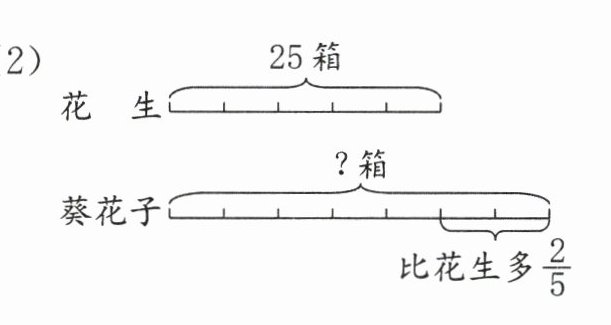
(2) $25×\left(1+\frac{2}{5}\right)=25×\frac{7}{5}=35$(箱)
(1) $600×\left(1-\frac{1}{4}-\frac{2}{5}\right)=600×\frac{7}{20}=210$(千米)
(2) $25×\left(1+\frac{2}{5}\right)=25×\frac{7}{5}=35$(箱)
1. 画一个长方形,周长是12厘米,长和宽的比是$2:1$,再在长方形内用你喜欢的方式表示$\frac {3}{4}×\frac {1}{2}$。(3分)


答案:
解析:本题考查按比例分配以及一个数乘分数的意义。
先根据长方形周长公式求出长和宽的和,再根据长和宽的比例分别求出长和宽,最后在长方形中表示出$\frac {3}{4}×\frac {1}{2}$。
长和宽的和:$12÷2 = 6$(厘米)
总份数:$2 + 1 = 3$(份)
长:$6×\frac{2}{3}= 4$(厘米)
宽:$6×\frac{1}{3}= 2$(厘米)
$\frac {3}{4}×\frac {1}{2}$表示求$\frac {3}{4}$的$\frac {1}{2}$是多少,可先把长方形平均分成$4$份,取其中的$3$份表示出$\frac {3}{4}$,再把这$\frac {3}{4}$平均分成$2$份,取其中的$1$份。
答案:图略(可先画一个长$4$厘米、宽$2$厘米的长方形,然后将长方形横向平均分成$4$个大长方形,取其中$3$个涂色表示$\frac{3}{4}$,再将涂色部分纵向平均分成$2$份,取其中$1$份再次涂色表示$\frac{3}{4}×\frac{1}{2}$ )。
先根据长方形周长公式求出长和宽的和,再根据长和宽的比例分别求出长和宽,最后在长方形中表示出$\frac {3}{4}×\frac {1}{2}$。
长和宽的和:$12÷2 = 6$(厘米)
总份数:$2 + 1 = 3$(份)
长:$6×\frac{2}{3}= 4$(厘米)
宽:$6×\frac{1}{3}= 2$(厘米)
$\frac {3}{4}×\frac {1}{2}$表示求$\frac {3}{4}$的$\frac {1}{2}$是多少,可先把长方形平均分成$4$份,取其中的$3$份表示出$\frac {3}{4}$,再把这$\frac {3}{4}$平均分成$2$份,取其中的$1$份。
答案:图略(可先画一个长$4$厘米、宽$2$厘米的长方形,然后将长方形横向平均分成$4$个大长方形,取其中$3$个涂色表示$\frac{3}{4}$,再将涂色部分纵向平均分成$2$份,取其中$1$份再次涂色表示$\frac{3}{4}×\frac{1}{2}$ )。
2. (1) 把第1题画出的长方形的长和宽分别增加$\frac {1}{2}$,画出增加的部分。(2分)
(2) 现在长方形的面积是原来长方形面积的$\frac {( )}{( )}$。(2分)
(2) 现在长方形的面积是原来长方形面积的$\frac {( )}{( )}$。(2分)
答案:
(1) 解析:
题目要求将长方形的长和宽分别增加$\frac{1}{2}$,然后画出增加的部分。
假设原始长方形的长为$l$,宽为$w$。
增加$\frac{1}{2}$后,新的长为$l × \left(1 + \frac{1}{2}\right) = \frac{3}{2}l$,新的宽为$w × \left(1 + \frac{1}{2}\right) = \frac{3}{2}w$。
增加的部分可以通过画出原始长方形和新的长方形,然后标注出增加的部分来完成。
由于这是一个画图题,所以在这里用文字描述:
画一个原始长方形,标注长为$l$,宽为$w$。
在原始长方形的右侧和下方,分别画出增加的长和宽的部分,使得新的长方形的长为$\frac{3}{2}l$,宽为$\frac{3}{2}w$。
增加的部分用阴影或其他标记表示出来。
答案:图略。
(2) 解析:
题目要求计算新的长方形的面积是原始长方形面积的多少倍。
原始长方形的面积为$l × w$。
新的长方形的面积为$\frac{3}{2}l × \frac{3}{2}w = \frac{9}{4}lw$。
所以,新的长方形的面积是原始长方形面积的$\frac{9}{4}$倍。
答案:$\frac{9}{4}$。
(1) 解析:
题目要求将长方形的长和宽分别增加$\frac{1}{2}$,然后画出增加的部分。
假设原始长方形的长为$l$,宽为$w$。
增加$\frac{1}{2}$后,新的长为$l × \left(1 + \frac{1}{2}\right) = \frac{3}{2}l$,新的宽为$w × \left(1 + \frac{1}{2}\right) = \frac{3}{2}w$。
增加的部分可以通过画出原始长方形和新的长方形,然后标注出增加的部分来完成。
由于这是一个画图题,所以在这里用文字描述:
画一个原始长方形,标注长为$l$,宽为$w$。
在原始长方形的右侧和下方,分别画出增加的长和宽的部分,使得新的长方形的长为$\frac{3}{2}l$,宽为$\frac{3}{2}w$。
增加的部分用阴影或其他标记表示出来。
答案:图略。
(2) 解析:
题目要求计算新的长方形的面积是原始长方形面积的多少倍。
原始长方形的面积为$l × w$。
新的长方形的面积为$\frac{3}{2}l × \frac{3}{2}w = \frac{9}{4}lw$。
所以,新的长方形的面积是原始长方形面积的$\frac{9}{4}$倍。
答案:$\frac{9}{4}$。
1. 根据问题在括号里列出算式,不计算。(4分)
有一批重20吨的货物,第一次运走总质量的$\frac {1}{5}$,第二次运走总质量的$\frac {1}{4}$。
(1) 第一次运走多少吨? ( )
(2) 还剩这批货物的几分之几? ( )
(3) 两次一共运走多少吨? ( )
(4) 第二次比第一次多运走多少吨? ( )
有一批重20吨的货物,第一次运走总质量的$\frac {1}{5}$,第二次运走总质量的$\frac {1}{4}$。
(1) 第一次运走多少吨? ( )
(2) 还剩这批货物的几分之几? ( )
(3) 两次一共运走多少吨? ( )
(4) 第二次比第一次多运走多少吨? ( )
答案:
解析:本题考查了分数的应用。
(1) 第一次运走多少吨?
根据题意,第一次运走了总质量的$\frac{1}{5}$,所以算式为:$20 × \frac{1}{5}$。
(2) 还剩这批货物的几分之几?
根据题意,第一次运走了总质量的$\frac{1}{5}$,第二次运走了总质量的$\frac{1}{4}$,所以算式为:$1 - \frac{1}{5} - \frac{1}{4}$。
(3) 两次一共运走多少吨?
根据题意,第一次运走了总质量的$\frac{1}{5}$,第二次运走了总质量的$\frac{1}{4}$,所以算式为:$20 × (\frac{1}{5} + \frac{1}{4})$。
(4) 第二次比第一次多运走多少吨?
根据题意,第二次比第一次多运走的吨数等于第二次运走的吨数减去第一次运走的吨数,所以算式为:$20 × \frac{1}{4} - 20 × \frac{1}{5}$。
答案:
(1) $20 × \frac{1}{5}$;
(2) $1 - \frac{1}{5} - \frac{1}{4}$;
(3) $20 × (\frac{1}{5} + \frac{1}{4})$;
(4) $20 × \frac{1}{4} - 20 × \frac{1}{5}$。
(1) 第一次运走多少吨?
根据题意,第一次运走了总质量的$\frac{1}{5}$,所以算式为:$20 × \frac{1}{5}$。
(2) 还剩这批货物的几分之几?
根据题意,第一次运走了总质量的$\frac{1}{5}$,第二次运走了总质量的$\frac{1}{4}$,所以算式为:$1 - \frac{1}{5} - \frac{1}{4}$。
(3) 两次一共运走多少吨?
根据题意,第一次运走了总质量的$\frac{1}{5}$,第二次运走了总质量的$\frac{1}{4}$,所以算式为:$20 × (\frac{1}{5} + \frac{1}{4})$。
(4) 第二次比第一次多运走多少吨?
根据题意,第二次比第一次多运走的吨数等于第二次运走的吨数减去第一次运走的吨数,所以算式为:$20 × \frac{1}{4} - 20 × \frac{1}{5}$。
答案:
(1) $20 × \frac{1}{5}$;
(2) $1 - \frac{1}{5} - \frac{1}{4}$;
(3) $20 × (\frac{1}{5} + \frac{1}{4})$;
(4) $20 × \frac{1}{4} - 20 × \frac{1}{5}$。
查看更多完整答案,请扫码查看


