11. 如图,在平面直角坐标系中,▱OABC的顶点A的坐标为(6,0),点C的坐标为(2,2).若直线$y=mx+2$平分▱ OABC的周长,则m的值为
$-\frac{1}{4}$
.
答案:
$-\frac{1}{4}$
12. 如图,在$\triangle ABC$中,$∠ACB=90^{\circ}$,$∠B=30^{\circ}$,$AC=6$,D是边CB上的动点,连接AD,将线段AD绕点A顺时针旋转$60^{\circ}$,得到线段AP,连接CP,则线段CP的最小值是
3
.
答案:
3
13. (10分)如图,在正方形网格中,将格点$\triangle ABC$(顶点为网格线的交点)绕某点顺时针旋转角$\alpha(0^{\circ}<\alpha<180^{\circ})$得到格点$\triangle A_1B_1C_1$.请通过画图找到旋转中心,将其标记为点O;旋转角$\alpha$的度数为____.


答案:
解:$90^{\circ}$.
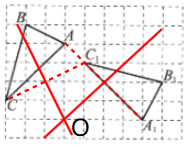
解:$90^{\circ}$.

14. (12分)如图,在正方形网格中,每个小正方形的边长都是1,$\triangle ABO$的三个顶点坐标分别为A(-1,3),B(-4,3),O(0,0).
(1)画出$\triangle ABO$关于原点O成中心对称的$\triangle A_1B_1O$,并写出点$A_1$的坐标;
(2)画出$\triangle ABO$绕点O顺时针旋转$90^{\circ}$后得到的$\triangle A_2B_2O$,并写出点$A_2$的坐标.

(1)画出$\triangle ABO$关于原点O成中心对称的$\triangle A_1B_1O$,并写出点$A_1$的坐标;
(2)画出$\triangle ABO$绕点O顺时针旋转$90^{\circ}$后得到的$\triangle A_2B_2O$,并写出点$A_2$的坐标.

答案:
解:
(1)点$A_{1}(1,-3)$.
(2)点$A_{2}(3,1)$.
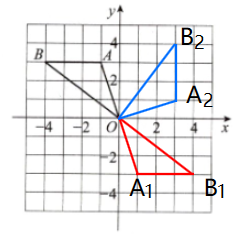
解:
(1)点$A_{1}(1,-3)$.
(2)点$A_{2}(3,1)$.

15. (12分)[2024·滁州全椒一模]如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段AB,点O在格点上.
(1)将线段AB绕点O顺时针旋转$90^{\circ}$得到线段CD,请画出线段CD;(点A的对应点为点C)
(2)以线段CD为一边,作一个正方形CDEF,且点E,F也为格点.(作出一个正方形即可)

(1)将线段AB绕点O顺时针旋转$90^{\circ}$得到线段CD,请画出线段CD;(点A的对应点为点C)
(2)以线段CD为一边,作一个正方形CDEF,且点E,F也为格点.(作出一个正方形即可)

答案:
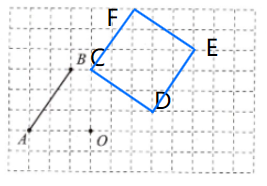

16. (14分)如图,在等腰$Rt\triangle ABC$中,$AB=BC$,$∠ABC=90^{\circ}$,点D在AC上,将$\triangle ABD$绕点B顺时针旋转$90^{\circ}$后,得到$\triangle CBE$.
(1)求$∠DCE$的度数;
(2)若$AB=4$,$CD=3AD$,求DE的长.

(1)求$∠DCE$的度数;
(2)若$AB=4$,$CD=3AD$,求DE的长.

答案:
解:
(1)$\angle DCE = 90^{\circ}$.
(2)$DE = 2\sqrt{5}$.
(1)$\angle DCE = 90^{\circ}$.
(2)$DE = 2\sqrt{5}$.
查看更多完整答案,请扫码查看


